Лекция № 13.

РЕШЕНИЕ НЕЛИНЕЙНЫХ СИСТЕМ УРАВНЕНИЙ.

Постановка задачи.

Введём

Найти приближение к – точное решение, такое что .

Выделяют два этапа:

1. Локализация корней.

2. Нахождение корня с заданной точностью.

Метод простой итерации (метод Якоби).

Пример.

Система для итераций.

Теорема 1.

Пусть в некоторой окрестности корня выполнены условия . Тогда МПИ сходится при любом начальном приближении и справедлива оценка:

Следствие 1.

Критерий окончания .

Для рассматриваемого примера.

Реализация решения на MathCAD.

Итерационные методы для решения систем нелинейных уравнений.

Метод Ньютона.

Пример.

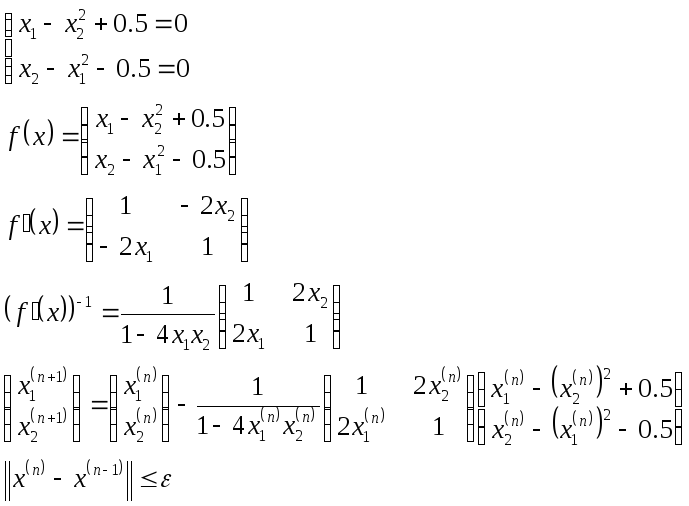
В силу громоздкости вычислений чаще используется упрощенный метод Ньютона.

Нелинейный метод Якоби.

Решаем уравнение как скалярное относительно .

Метод Зейделя (нелинейный).

Модификация нелинейного метода Якоби.

Метод простой итерации в канонической форме.

Метод Ньютона-Зейделя.

Метод Пикара.

Пример.

Получили СЛАУ с одной и той же матрицей A и разными правыми частями на каждой n-ой итерации.

Лекция № 14.

РЕШЕНИЕ ПЕРЕОПРЕДЕЛЁННЫХ СИСТЕМ.

Линейная задача.

Переопределённая система – число уравнений больше числа неизвестных.

Определение 1.

Будем называть A матрицей полного столбцевого ранга, если .

–матрица полного столбцевого ранга, – единственное решение.

Определение 2.

Будем называть вектором невязки .

–решение системы, в общем случае не существует.

Понимаем под решением задачи вектор .

Теорема 1.

Решением задачи является вектор , удовлетворяющий системе уравнений .



Если – решение системы , то ­ – точка .

Пример.

Докажем, что ­– симметричная и положительно определена.





Утверждение 1.

для матриц полного столбцевого ранга имеет единственное решение.



Нелинейная задача метода наименьших квадратов.

Сведём к линейной задаче, выполнив линеаризацию по Ньютону:

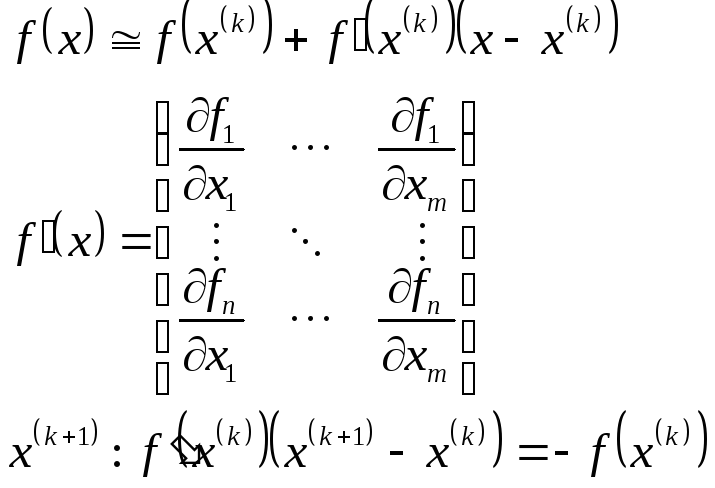
Критерий окончания

Вводится вектор поправки:

Алгоритм решения:

Найдена . Вычисляем .

Получаем .

Упрощённый метод Ньютона.

Пример.

Постановка задачи минимизации функций.

Необходимое условие экстремума .

Определение 3.

Методы, использующие производные, называются градиентными.

Определение 4.

называется унимодальной на , если существует , для которого выполняются условия:

Определение 5.

Точка ­– точка локального минимума, если в определении точки выполняется условие .

Метод биекции поиска точки минимума.

Утверждение 2.

Пусть внутри и . Если , то берём отрезок , иначе .

Алгоритм метода биекции аналогичен методу половинного деления с выбором параметра итерационного процесса .

Лекция № 15.

МЕТОДЫ МИНИМИЗАЦИИ.

Методы поиска.

Утверждение 1.

Сужение отрезка унимодальных функций.

Если , то , в противном случае .

Пассивный поиск.

Если , то оптимальный поиск .

Метод биекции.

Применяем утверждение о сужении отрезка.

Если , то , в противном случае .

Теорема 1.

Пусть – унимодальная на и . Тогда справедлива оценка .

Доказывается методом индукции.



Метод золотого сечения.

Определение 1.

Золотым сечением отрезка называется деление отрезка в отношении .

Алгоритм метода золотого сечения:

Пусть на k-ом шаге выбран отрезок . Тогда либо , либо . Сужение отрезка в соответствии с утверждением.

Критерий окончания , но при этом берётся равным .

Оценка погрешности метода .