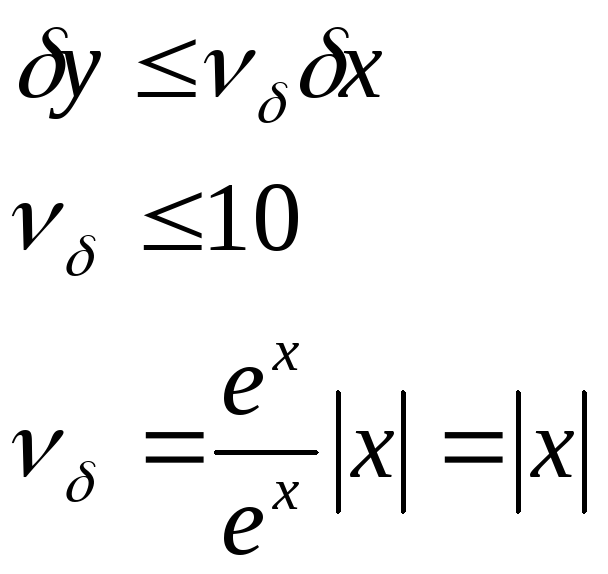- •Численные методы
- •Правила округления.
- •Оценка погрешностей арифметических операций и функций.
- •Оценка погрешности функции одной переменной.
- •Лекция № 2. Особенности машинной арифметики. Корректность вычислительной задачи.
- •Принцип равных влияний.
- •Представление данных в эвм.
- •Нелинейные уравнения.
- •Метод простой итерации (мпи).
- •Универсальный алгоритм приведения уравнения к виду,
- •Лекция № 5.
- •Обусловленность задачи решения слау.
- •Лекция № 6. Решение слау прямыми методами. Метод Гаусса и его модификации.
- •Модификации метода Гаусса.
- •Lu-разложение или матричная форма метода Гаусса.
- •Применение прямых методов для решения слау.
- •Метод простой итерации.
- •Лекция № 8.
- •Лекция № 9.
- •Лекция № 10.
- •Итерационный процесс
- •С чебышевским набором параметров.
- •Многочлены Чебышёва.
- •Вспомогательная задача.
- •Чебышёвский процесс для вычисления решения системы.
- •Лекция № 11.
- •Лекция № 13.
- •Нелинейная задача метода наименьших квадратов.
- •Метод Фибоначчи.
- •Градиентные методы.
МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ
(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
Лекции
Численные методы
4 семестр
Лектор Амосова Ольга Алексеевна
Москва, 2009/2010
Лекция № 1.
 ОСНОВНЫЕ
ТИПЫ ПОГРЕШНОСТЕЙ.
ОСНОВНЫЕ
ТИПЫ ПОГРЕШНОСТЕЙ.
Классификация погрешностей.
Целые ответы – огромная редкость.
Основные типы погрешностей:
Неустранимые погрешности (погрешность модели, входных данных).
Погрешность метода (использование алгоритмов для решения задачи).
Вычислительная погрешность (при вычислениях на компьютерах).
Пример.

![]()
Неточности: не учитывается сопротивление воздуха и т. п.
Метод (извлечение корня) – алгоритм Ньютона.
Определение 1.
Пусть а
– точное
значение,
![]() – приближенное значение той же величины,
тогда:
– приближенное значение той же величины,
тогда:
Абсолютной
погрешностью
называется величина ![]() (1)
(1)
Относительной
погрешностью называется
величина ![]() (2)
(2)
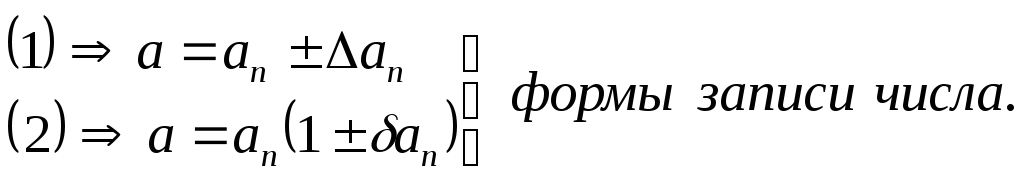
Пример.

Определение 2.
Значащей цифрой числа называются все цифры в его записи, начиная с первой ненулевой слева.
![]()
Определение 3.
Значащая цифра называется верной, если абсолютная погрешность числа не превышает единицы разряда, соответствующего этой цифре.
Пример.

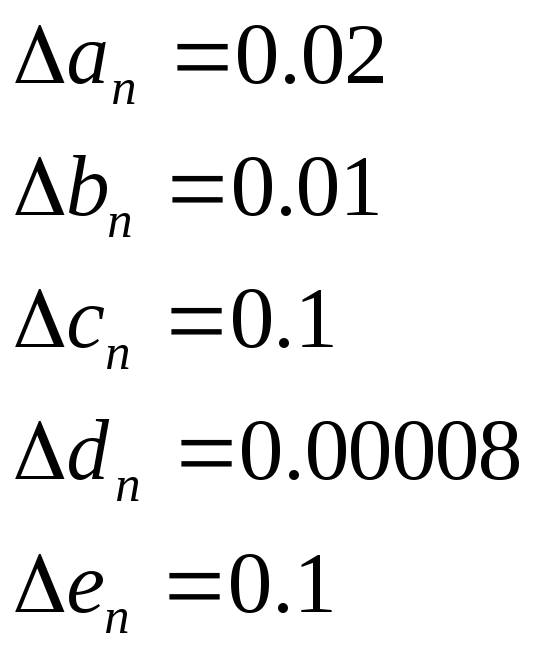
Правила округления.
Правила округления:
Округление усечением.
![]()
Округлим до k-ого
разряда вне зависимости от
![]() .
.
![]()
Округление по дополнению.
![]()
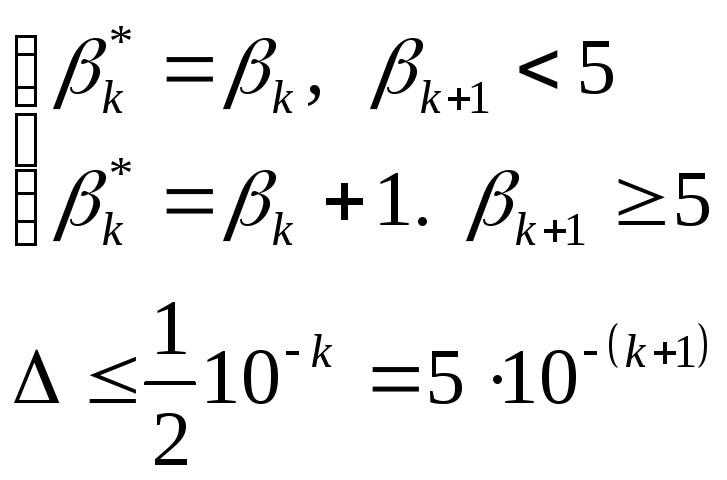
Договоримся, что, если число задано без погрешности, то абсолютная погрешность числа равна половине оставленного разряда.
![]()
Определение 4.
Нормальная форма записи числа
![]() .
.
![]()
![]() –мантисса числа,
p
– порядок
числа.
–мантисса числа,
p
– порядок
числа.

Пример.
![]()
Оценка погрешностей арифметических операций и функций.
Утверждение 1.
Абсолютная
погрешность ![]() не превышает абсолютных погрешностей
аргументов.
не превышает абсолютных погрешностей
аргументов.
![]()
Утверждение 2.
Относительная погрешность произведения и частного не превышает суммы относительных погрешностей аргументов.
![]()
Оценка погрешности функции одной переменной.
Дана функция ![]() .
.
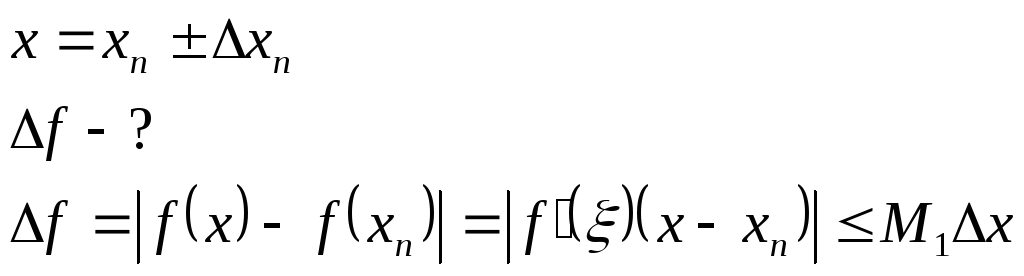
![]() на отрезке,
содержащем
на отрезке,
содержащем ![]() и
и ![]() .
.
Пример.
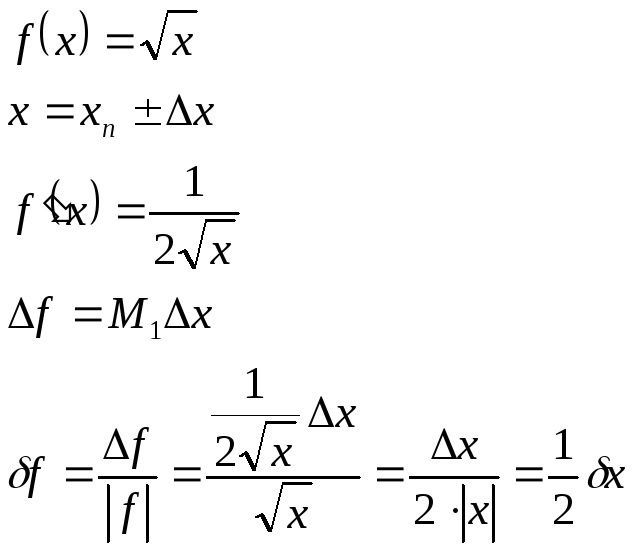
Основная задача теории погрешностей:
Дана функция m переменных
![]()
Требуется найти
![]() .
.
Теорема 1.
Если функция непрерывно дифференцируема по любому аргументу, то верна общая формула погрешностей:
![]() (3)
(3)
Запишем следующую формулу (2 члена приближения формулы Тейлора):
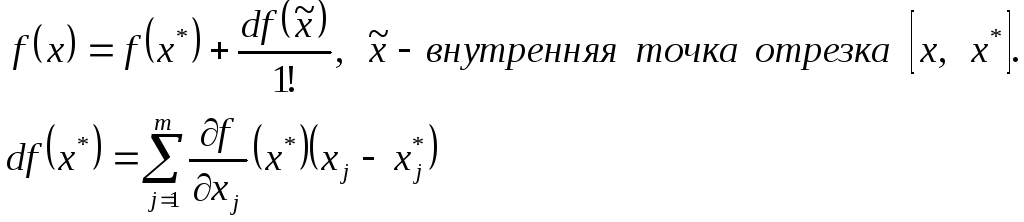
![]()
Пример.

Определение 5.
Будем называть
абсолютным
числом обусловленности
число ![]() ,
удовлетворяющее
,
удовлетворяющее ![]() и относительным
числом обусловленности
число
и относительным
числом обусловленности
число ![]() ,
удовлетворяющее
,
удовлетворяющее ![]() ,
где
,
где
![]() –абсолютная и
относительная погрешности входного
данного;
–абсолютная и
относительная погрешности входного
данного;
![]() –абсолютная и
относительная погрешности результата.
–абсолютная и
относительная погрешности результата.
Определение 6.
Будем называть
задачу хорошо
обусловленной,
если относительное число обусловленности
![]() и плохо
обусловленной
– в противном случае.
и плохо
обусловленной
– в противном случае.
Лекция № 2. Особенности машинной арифметики. Корректность вычислительной задачи.
Определение 1.
Будем называть вычислительную задачу корректной по Адамару, если:
Решение существует для всех допустимых входных данных.
Решение задачи устойчиво, т. е. непрерывным образом зависит от входных данных (малой погрешности входных данных соответствует малая погрешность результата).
Решение задачи единственно.
Пример.
![]()
По правилу Крамера
![]() решение
существует и единственно
решение
существует и единственно![]() .
.
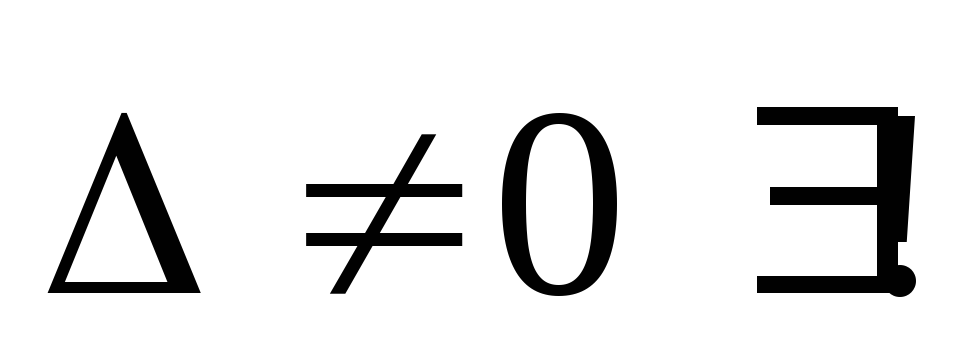
 неопределенность
неопределенность
 задача некорректна.
задача некорректна.
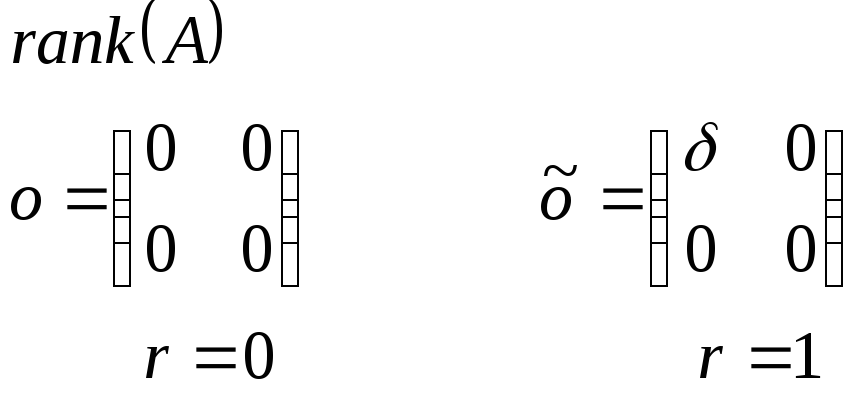
Задача не является корректной.
Задача вычисления
интеграла непрерывной функции
![]() .
.
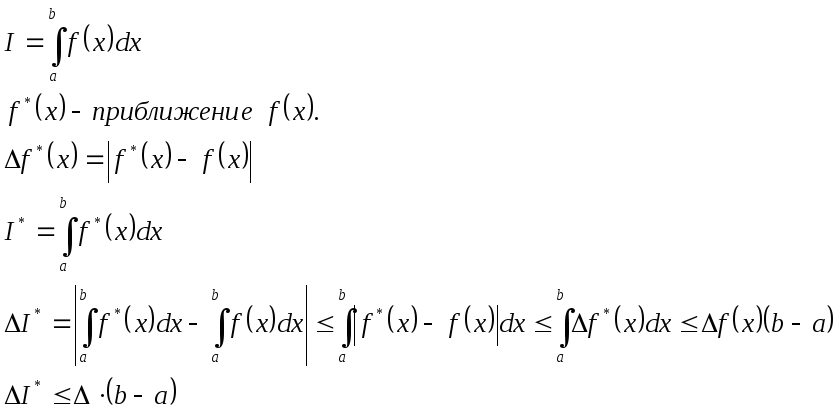
![]() –погрешность
входных данных.
–погрешность
входных данных.
![]()
Пусть ![]() – множество входных данных,
– множество входных данных, ![]() – множество решений.
– множество решений.
![]() –числа обусловленности
задачи.
–числа обусловленности
задачи.
![]()
В задаче вычисления
интеграла получили
![]() .
.
Найдём относительное число обусловленности задачи

Если
![]() ,
то задача хорошо обусловлена.
,
то задача хорошо обусловлена.
Если
![]() – осциллирующая (например,sin
с малым периодом), то
– осциллирующая (например,sin
с малым периодом), то
![]() .
.
Найдём оценку числа обусловленности вычисления функции одной переменной.
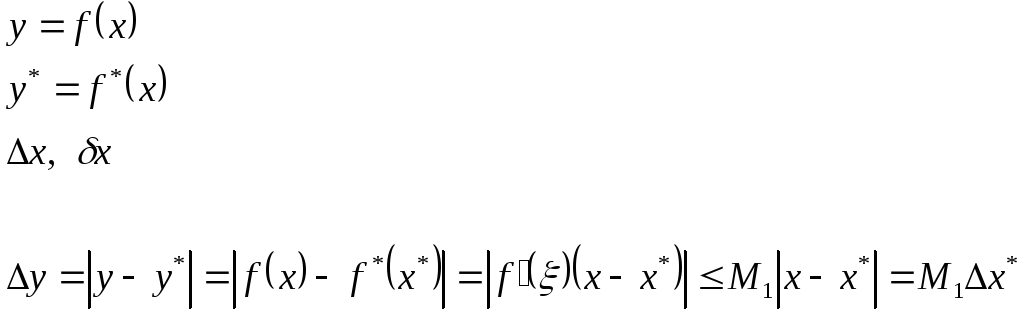
![]() –абсолютное число
обусловленности.
–абсолютное число
обусловленности.
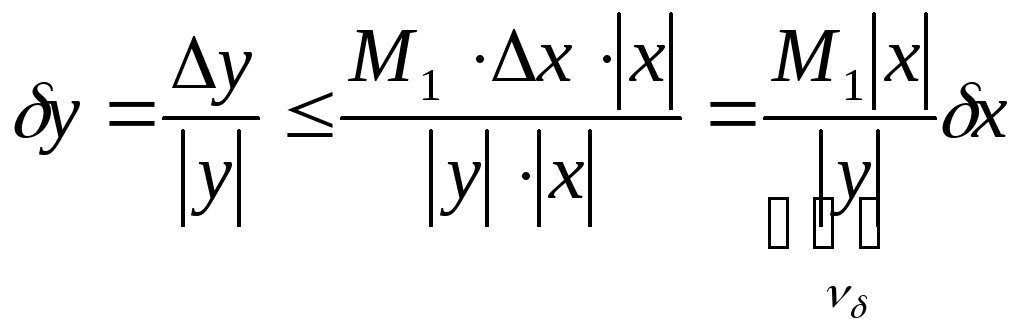
Пример.
При каких значениях
x
задача вычисления функции ![]() является хорошо обусловленной задачей?
является хорошо обусловленной задачей?