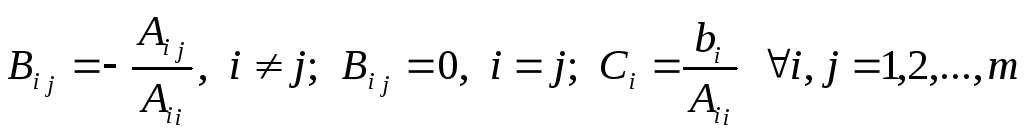Применение прямых методов для решения слау.
Метод частичного выбора (однократное вычисление системы).
система с разными
правыми частями.
Если нашли
,
то решаем фактически 
.
метод Холецкого.A разреженная. Метод прогонки.
Метод простой итерации.
Расчётные формулы:
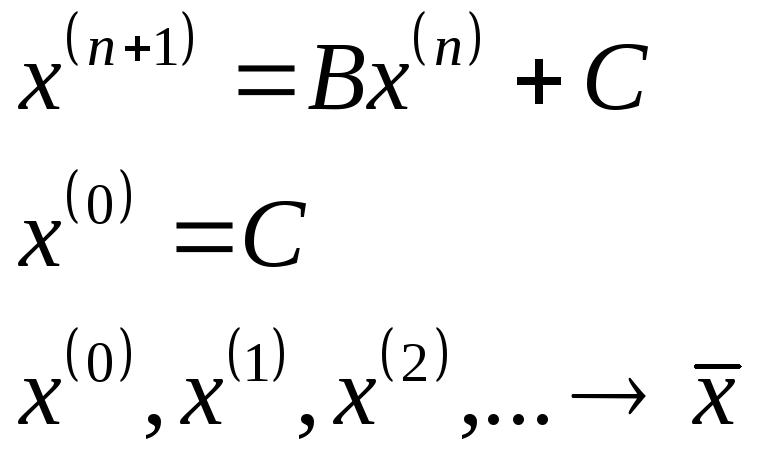
Пример.
Покоординатная форма записи для МПИ:
Теорема 2.
О достаточном условии сходимости МПИ.
Пусть рассматривается
МПИ 
и пусть выполняется условие 
.
Тогда МПИ сходится при любом начальном
приближении и справедливы оценки:
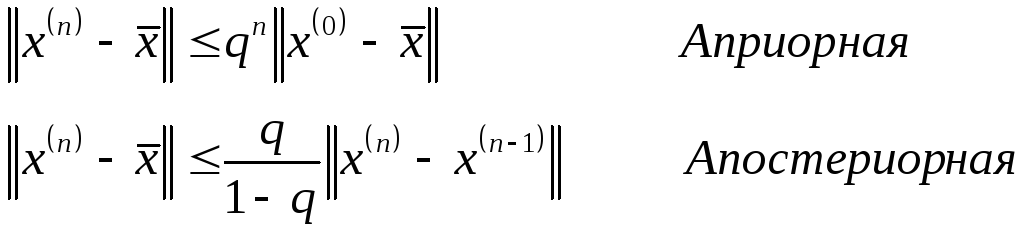
–решение системы
.
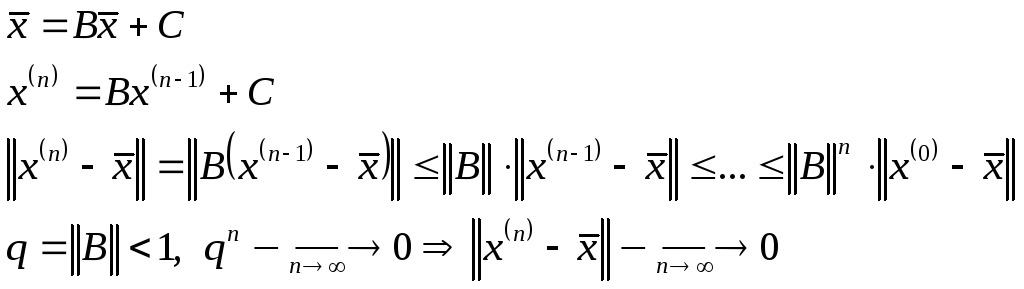
Следствие.
Критерий окончания МПИ:
,
где 
– заданная точность.
Существуют две формы записи МПИ:
Матричная форма.
Покоординатная форма.
Если матрица B
обладает свойством диагонального
преобладания 
,
то можно доказать, что 
.
Иногда диагональное преобладание можно получить, переставляя строки в исходной системе уравнений.
Лекция № 8.
РЕАЛИЗАЦИЯ
МПИ НА MathCAD.
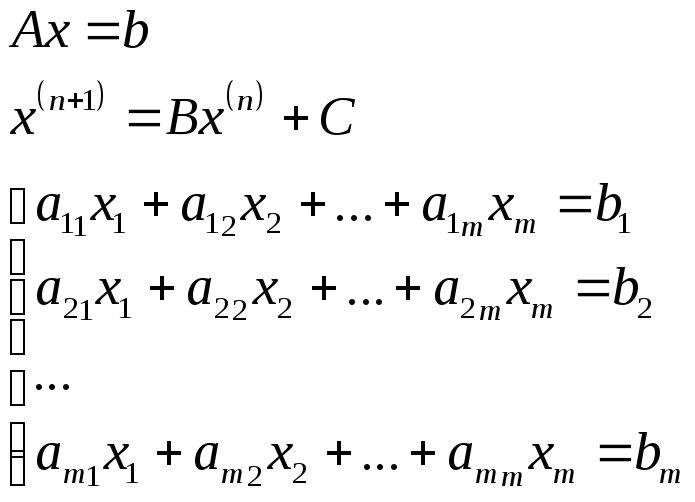
Алгоритм:
Вычисление
по МПИ с заданной точностью 
.
Методы Зейделя и релаксации.
Покоординатная форма записи метода Зейделя.
Матричная форма записи метода Зейделя.
Достаточное условие
сходимости МПИ 
.
Достаточное условие
сходимости МЗ 
.
Теорема 1.
Пусть рассматривается
метод Зейделя 
.
Тогда если 
,
то метод Зейделя сходится при любом
начальном приближении и справедливы
следующие оценки:
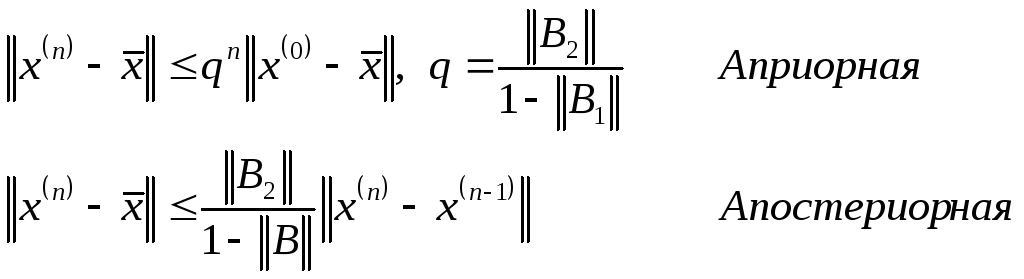
Следствие 1.
Метод Зейделя сходится со скоростью геометрической прогрессии.
Следствие 2.
Критерий окончания
.
Геометрическая интерпретация метода Зейделя.
Замечание.
Метод Зейделя может зациклиться.
SOR метод (верхней релаксации).
Каноническая форма записи итерационных методов.
Определение 1.
Канонической формой итерационного метода общего вида называется:
Если 
,
то метод называется неявным,
иначе – явным.
Если 
зависят от номера итерации, то метод
называется итерационным,
иначе – стационарным.
B – итерационная матрица.
–итерационный
параметр.
Вектор погрешности
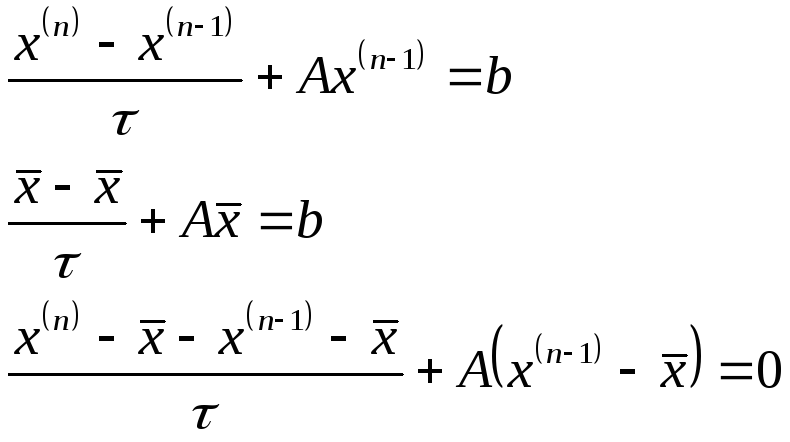
Вектор ошибки
удовлетворяет уравнению 
Определение 2.
называется матрицей
перехода от
вектора погрешности от 
к 
для МПИ 
.
Теорема 2.
Если все собственные
числа 
матрицы S
,
то метод итерационно сходится при любом
начальном приближении.
Необходимость
Достаточность
Предположим дополнительно, что S имеет собственные векторы, образующие собственный базис.
Лекция № 9.
ИТЕРАЦИОННЫЕ
МЕТОДЫ
ДЛЯ ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЁННЫХ МАТРИЦ.
Итерационные методы в канонической форме.
Критерий Сильвестра:
Запишем наиболее распространённые методы в канонической форме:
Метод Якоби.
Метод релаксации.
–параметр, берётся
всегда положительным.
Метод Зейделя
.
Условия сходимости итерационных методов
для симметричных, положительно определённых матриц.
Теорема 1.
Пусть 
и 
.
Тогда итерационный метод сходится при
любом начальном приближении.
Докажем, что
.
Рассмотрим
числовую последовательность 
.
Докажем, что 
убывает.
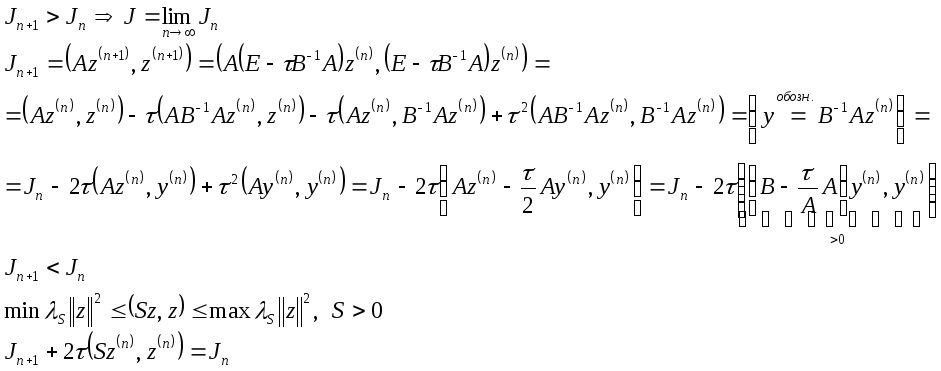
Следствие 1.
Пусть матрица A
обладает свойством диагонального
преобладания, т. е. 
.
Тогда метод Якоби сходится при любом
начальном приближении.
.
Следствие 2.
Если 
,
то метод релаксации 
и, в частности метод Зейделя 
,
сходится при любом начальном приближении.
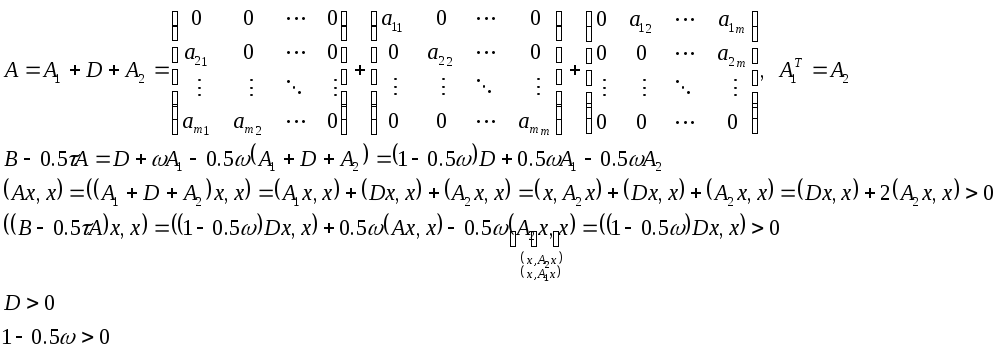
Утверждение 1.
Пусть 
и 
– спектр матрицы. Тогда метод простой
итерации 
сходится при 
и любом начальном приближении.
Пусть
,
тогда метод сходится при любом начальном
приближении.
Если
– собственные
числа A,
то
.
Если
–собственный
вектор.
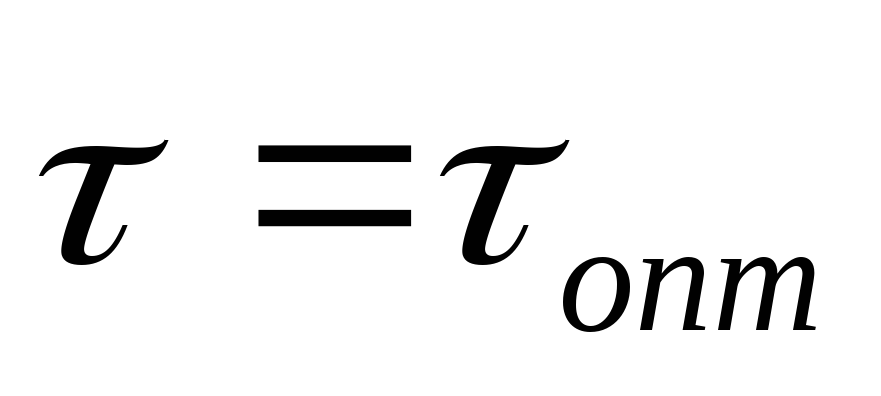минимальная
погрешность метода;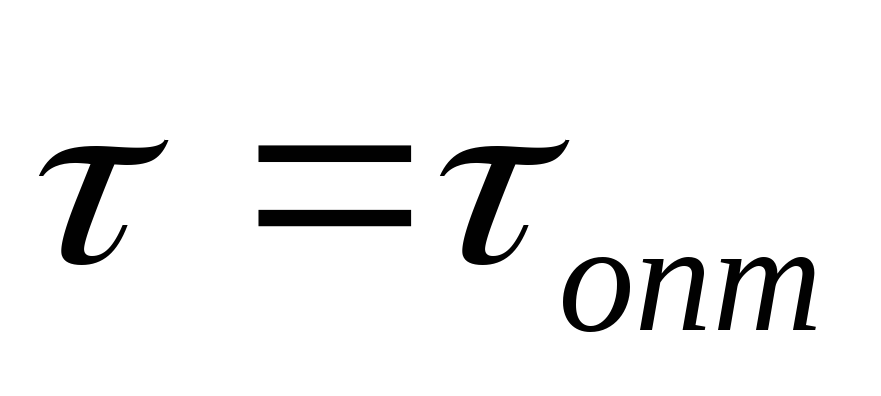
метод сходится.
Замечание.
В МПИ необходимым
и достаточным условием выбора параметра
является
.