
Лекции (2010)
.pdfМОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ (ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
Лекции
ЧИСЛЕННЫЕ МЕТОДЫ
5 семестр
Лектор Амосова Ольга Алексеевна
Москва, 2010/2011

Лекция № 1.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ (МНК).
Постановки задач.
Имеем дискретное множество точек x0 , x1, ... , xn и в этих точках заданы
f0 , f1, ..., fn .
f x x – аппроксимация.
x C0 0 x C1 1 x ... Cm m x – обобщѐнный многочлен.k x – базисные функции:
1.Многочлены 1, x, x2 , ... , xk ;
2.Тригонометрические sin nx, cos nx ;
3.Экспоненциальные ekx .
Существует два способа приближения:
1.Приближение в «среднем» применяется в случае, если известно, что данные получены с ошибками (метод сглаживает неточности).
2.Приближение методом интерполяции применяется для точных данных.
y |
y |
x |
x |
x0 |
x1 |
... |
xn x |
x0 |
x1 |
... |
xn x |
Рис. 1. Приближение в «среднем». |
Рис. 2. Приближение методом |
||||||
|
|
|
|
|
интерполяции. |
|
|
1 | С т р а н и ц а

Алгоритм метода наименьших квадратов.
Постановка задачи. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Дано: |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|||
x0 , |
x1, ... , |
xn |
– n+1 узел. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
x |
|||||||||||
y0 , |
y1, ... , |
yn |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Требуется |
найти полином |
степени m P |
x , |
|
0 |
1 |
|
|
n |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
минимизирующий |
|
|
|
|
среднеквадратичное |
|
|
|
|
|
|
|
|||||||
отклонение |
|
|
|
(СКО) |
функции |
x0 |
|
x1 |
... |
|
xn x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
n |
y P x |
|
. Обычно m n . |
|
Рис. 3. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||||
|
i 0 |
|
|
0 |
1 ... |
n |
|
||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
2 |
2 |
|
2 |
min |
||||
|
|
n 1 |
i m i |
|
|
|
|
|
|
|
|
|
|
n 1 |
|
||||
Заметим, что a0 , |
|
a1, ... , |
am . |
|
|
|
|
|
|
|
|
||||||||
Условие экстремума |
|
|
|
0, |
k 0,1,..., m . |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
Очевидно, что a0 ,
той же точке, что и .
Условие экстремума.
n |
Pm xi |
|
n |
m |
2 |
|
a1, ..., am yi |
yi |
a j xi |
имеет минимум в |
|||
|
|
2 |
|
|
j |
|
i 0 |
|
|
i 0 |
j 0 |
|
|
a0 , a1, ..., |
n |
Pm xi |
|
n |
m |
2 |
am yi |
yi |
a j xi |
||||
|
|
|
2 |
|
|
j |
|
i 0 |
|
|
i 0 |
j 0 |
|
|
|
|
|
|
n |
|
m |
|
|
j |
|
|
|
|
|
|
|
n |
|
m |
k |
j |
|
n |
k |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 yi a j xi |
xi |
0 a j xi |
|
yi xi |
|
, k 0,1,..., m |
|
||||||||||||||||||||||
|
ak |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
i 0 |
|
j 0 |
|
|
|
|
|
|
|
|
|
i 0 j 0 |
|
|
i 0 |
|
|
|
|
|
|
|
||||||
|
|
|
n |
|
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
xi0 |
a1 xi1 |
a2 xi2 |
... |
am xim |
yi xi0 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
a0 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
i 0 |
|
|
i 0 |
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|
i 0 |
|
|
i 0 |
|
|
|
|
|
обозн. n |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
n |
1 |
|
n |
2 |
|
|
n |
3 |
|
|
|
|
|
|
|
|
n |
m 1 |
n |
|
1 |
|
Sk |
|
xik |
||||
|
|
a0 |
xi |
a1 xi |
a2 xi |
... am xi |
|
yi xi |
|
|
|
|
i 0 |
|
||||||||||||||||||
|
i 0 |
|
i 0 |
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|
i 0 |
|
|
i 0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
обозн. |
n |
||||||||||||||
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bk |
|
yi xik |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 0 |
|
|
|
|
n |
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
xim a1 |
xim 1 a2 xim 2 |
|
... am xi2m |
yi xim |
|
|
|
|
||||||||||||||||||||||
|
|
a0 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
i 0 |
|
|
i 0 |
|
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|
i 0 |
|
|
i 0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
S |
a |
S a ... S |
m |
a |
m |
|
b |
|
|
a |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
0 0 |
|
1 |
1 |
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b1 |
|
|
a1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
S1a0 S2a1 ... Sm 1am |
|
|
|
|
|
|
|
|
||||||||||||||||||
Гa b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pm x |
|
|
|
|
|||||||||||
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
S |
a |
S |
|
a ... S |
2m |
a |
m |
b |
|
a |
m |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
m 0 |
|
|
m 1 1 |
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
m |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
Нормальная система МНК a j xik j |
yi xik , |
k 0,1,..., m . |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 0 |
j 0 |
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|||||
Г – матрица нормальной системы МНК.
2 | С т р а н и ц а

Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рассмотрим функцию, заданную таблично. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
-2 |
-1 |
0 |
1 |
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yi |
|
-2 |
0 |
-1 |
1 |
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
x |
|
-1.4 -0.9 |
-0.4 |
0.1 |
0.6 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
i |
|
|
|
|
|
|
|
|
|||||||
|
1. P0 x |
|
a0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
P x |
|||||
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
P2 x |
|
|
|
|
|||||||
|
|
S0a0 b0 |
a0 |
|
0 |
0.4 |
|
|
|
|
|
|
|
1 |
1 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
S0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
P0 x 0.4 0.5x |
|
|
|
|
|
|
-2 |
-1 |
0 |
|
1 |
2 x |
|||||||||||||||
|
2. P x |
a |
a x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P0 x |
|
||||||||
|
|
1 |
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|||
|
|
S |
a |
|
S a |
b |
|
|
|
5a |
2 |
|
a |
0.4 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
0 0 |
|
1 1 |
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
S1a0 |
|
S2a1 |
b1 |
|
|
|
10a1 5 |
|
a1 |
0.5 |
|
|
|
|
|
|
|
|
|
-2 |
|
|
|||||
|
|
P x |
0.4 0.5x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
P x |
|
0.03 0.5x 0.214x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
2 1.4 2 0 0.9 2 1 0.4 2 1 0.1 2 0 0.6 2 |
|
0.73 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
0.64 наименьшее качество приближения лучше |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
В реальных задачах МНК применяется до степеней m 5 . В силу плохой обусловленности системы МНК. Качество приближения вычисляется по величине СКО.
Теорема 1.
Многочлен СКО существует и единственен.
m
Рассматриваем Pm x a j x j .
j 0
Докажем, что однородная нормальная система МНК имеет только нулевое решение, т. е. Pm x 0 .
n |
m |
|
|
|
|
|
|
|
|
a j xik j 0, |
k 0,1,..., m |
|
|
|
|
|
|
|
|
i 0 |
j 0 |
|
|
|
|
|
|
|
|
Умножим каждое k-ое уравнение на ak и просуммируем. |
|
|
|||||||
|
|
|
|
|
|
Pm x0 0 |
|
||
|
|
|
|
|
|
|
x1 0 |
|
|
m |
n m |
n m |
m |
n |
|
Pm |
m n Pm x 0 |
||
ak a j xik j 0 ak xik a j xij Pm2 |
xi |
0 |
|
|
|||||
k 0 |
i 0 j 0 |
i 0 k 0 |
j 0 |
i 0 |
|
... |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
x |
|
|
||
|
|
Pm xi |
Pm xi |
|
|
P |
0 |
|
|
|
|
|
|
|
|
m |
n |
|
|
Докажем, что Pm x действительно минимизирует СКО.
m
Рассмотрим произвольный многочлен Qm x bj x j .
j 0
3 | С т р а н и ц а

|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
Qm |
Qm |
xi |
yi 2 Qm |
xi Pm xi Pm xi yi 2 Qm xi Pm xi 2 |
||||||||||||||||||||
|
|
|
i 0 |
|
|
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|
i 0 |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
2 Qm xi Pm |
xi Pm xi yi |
Pm xi yi 2 |
|
|
|
|
|
|
|
|||||||||||||||
i 0 |
|
|
|
|
|
|
|
|
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
Pm |
|
|
|
|
|
|
|
|
|
|
n m |
k |
|
m |
k |
m |
|
|
j |
|
|
|
n m |
b |
m |
|
k j |
|
k |
|
||||
A |
|
|
|
b x |
|
a x |
|
|
a |
x y |
|
|
|
|
|
a x |
|
y x |
|
|
||||
|
|
|
|
|
i |
|
a |
|
|
|
|
|||||||||||||
|
|
k i |
|
k i |
|
j |
|
i |
|
|
k |
k |
j i |
i i |
||||||||||
|
i 0 |
k 0 |
|
|
k 0 |
|
j 0 |
|
|
|
|
|
|
i 0 k 0 |
|
|
j 0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Qm |
Qm |
xi |
Pm xi 2 Pm |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
i 0 |
|
|
|
достигается при Qm x Pm x . |
|
|
|
|
|
||||||||||||
Минимум Qm |
|
|
|
|
|
|
||||||||||||||||||
4 | С т р а н и ц а

Выбор другой системы базисных функций.
m
m x C j j x
j 0
Минимизируется следующая величина C0 ,
Условия экстремума (необходимое условие)
Гc b
Г – нормальная система МНК.
|
n |
|
m |
2 |
|
|
|
C j j xi |
|
C1, ..., Cm yi |
. |
|||
|
i 0 |
|
j 0 |
|
|
0 . |
|
|
|
|
|
|
|
|
Ck |
|
|
|
|
5 | С т р а н и ц а

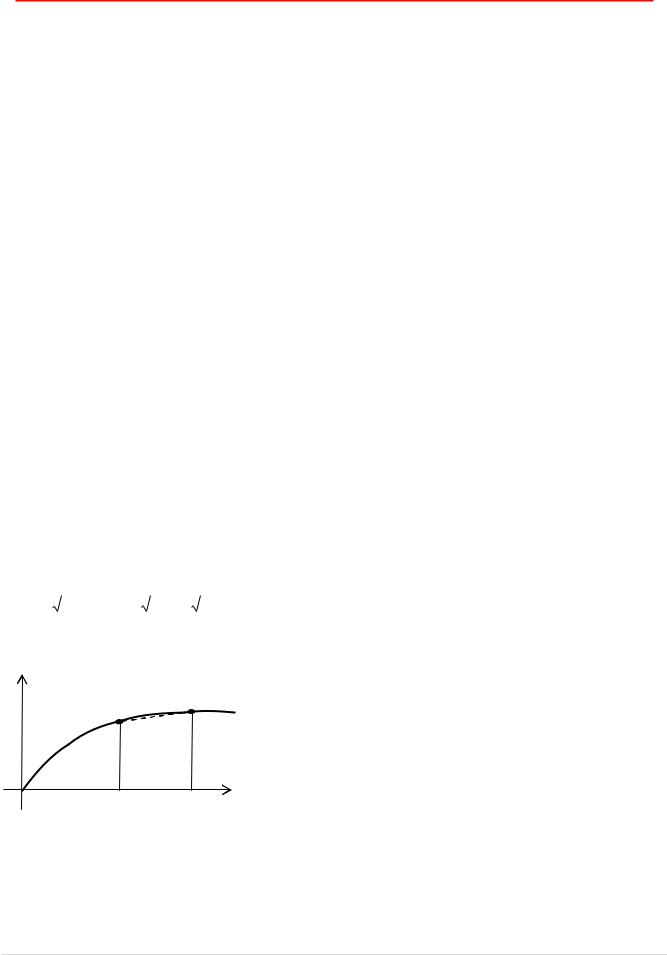
Выбор степени m.
1.Дискретная функция приближается по МНК.
– заданная точность.
m
m 0 0
...
mm* m* m* оптимальна.
2.Дискретная функция приближается по МНК.
участок
нормализации
1 2 3 ... m* m
Рис. 4. Выбор наилучшей степени m.
6 | С т р а н и ц а
Лекция № 2.
ПРИБЛИЖЕНИЕ ФУНКЦИИ МЕТОДОМ ИНТЕРПОЛЯЦИИ.
Многочлен Лагранжа.
Дано: x0 , |
x1, ... , xn и y0 , y1, ... , yn . Требуется построить многочлен степени n |
Pn : Pn xi |
yi , i 0,1,..., n |
Теорема 1.
Интерполяционный многочлен существует и единственен.
Рассмотрим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n |
n |
x x |
|
|
x x |
|
x x ... x x |
|
|
|
x x |
x x ... x x |
|
|
|||||||||
Ln x yi |
k |
|
|
y0 |
|
1 |
|
2 |
|
n |
|
|
... yn |
|
0 |
|
1 |
|
n 1 |
|
|
||
x x |
|
x |
x |
x |
x |
... x |
x |
|
x |
x x |
x |
... x |
x |
|
|
||||||||
i 0 |
k 0 |
|
|
|
|||||||||||||||||||
i k |
|
|
|
0 |
1 |
|
0 |
2 |
0 |
n |
|
n |
0 |
n |
1 |
n |
n 1 |
|
|||||
|
k i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
многочлен Лагранжа n-ой степени, содержит n+1 слагаемое и удовлетворяет условиям интерполяции:
Ln xi yi , i 0,1,..., n
Докажем единственность. |
|
|
|
|||||||||||
Пусть L1 |
x , L2 x и L x L1 |
x L2 x . |
|
|
||||||||||
|
|
|
n |
n |
|
|
|
|
|
n |
n |
|
|
|
Степень многочлена L x меньше или равна n. |
|
|
||||||||||||
L x L1 |
x |
L2 |
x |
y y 0 |
|
|
|
|||||||
i |
n |
|
i |
n |
i |
|
|
i |
i |
|
|
|
||
Следовательно, |
узлы xi – корни L x , их n+1 |
штук. Значит, L x |
обращается в |
|||||||||||
ноль |
в |
n+1 |
точке. |
Следовательно |
L x 0 . Отсюда |
и вытекает |
||||||||
единственность. |
|
|
|
|
|
|
||||||||
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|||
f x |
|
|
|
|
|
|
|
|
|
|
|
|||
x . Найти |
11 и |
14 . |
|
|
|
|||||||||
x0 9 |
y0 3 |
|
|
|
|
|
|
|
|
|
|
|||
x1 11 |
y1 4 |
|
|
|
|
|
|
|
|
|
|
|||
y
|
|
|
|
|
9 |
|
16 |
x |
|||
L |
|
x 3 |
x 16 |
|
4 |
x 9 |
|
3 |
x 16 |
4 |
x 9 |
|
|
|
|
|
|||||||
1 |
|
9 16 |
16 9 |
7 |
7 |
|
|||||
|
|
|
|
||||||||
L1 |
11 3.2857 |
|
|
|
|
|
|
|
|||
f |
11 3.3166 |
|
|
|
|
|
|
|
|||
R 11 f 11 L1 11 0.03
R 14 0.027
7 | С т р а н и ц а
Определение 1.
Экстраполяция – вычисление значений функции с помощью интерполяционного многочлена вне отрезка x0 ; xn .
Определение 2.
Погрешностью интерполяции R называется разность между исходной функцией и построенным интерполяционным многочленом.
Теорема 2.
Пусть f x Cn 1 x0 ; xn ,
n
n 1 x x xi .
i 0
тогда R x |
|
f x L x |
|
|
Mn 1 |
|
|
|
|
x |
|
, M |
|
max |
|
f n 1 x |
|
, |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
n 1 ! |
n 1 |
n 1 |
||||||||||||||
n |
|
n |
|
|
|
|
|
|
|
x0 ; xn |
|
|
|
|
||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
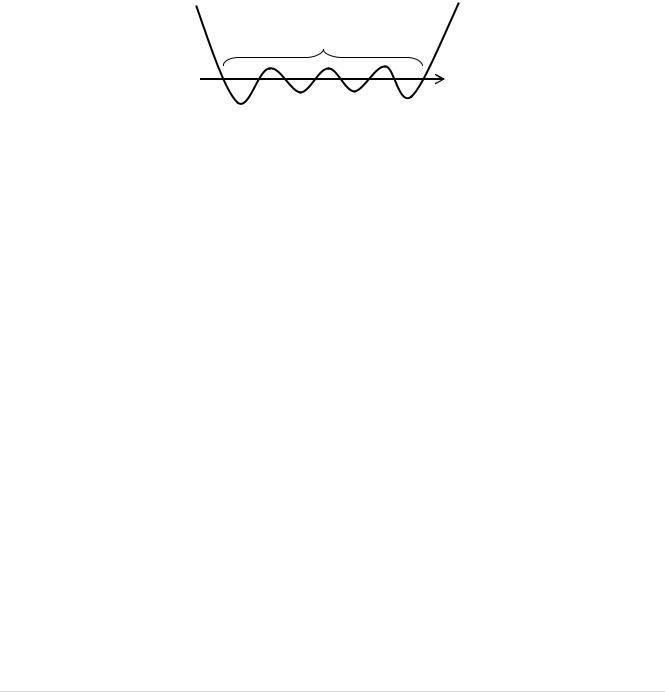
 Сильный рост
Сильный рост  Небольшая амплитуда
Небольшая амплитуда
x0 x1 x2 ... xn x
Следствие. |
|
|||
Будем |
называть узлы равномерными, если xi xi 1 h, h шаг . Тогда |
|||
R x |
M n 1 |
|
hn 1 . |
|
4 n 1 ! |
||||
n |
|
|||
|
|
|||
8 | С т р а н и ц а

Минимизация погрешности интерполяции.
Многочлены Чебышева Tn x 2xTn 1 x Tn 2 x .
T0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
T1 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
T |
|
|
2x2 1 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1;1 : Tn x cos n arccos x |
|||||||||||||||||||||||
x |
|
|
cos |
|
|
|
2k 1 |
, |
k 0,1,..., n |
||||||||||||||
k |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2n 2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1;1 a; b |
x |
a b |
t |
b a |
|||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
||
t |
|
|
|
cos |
|
|
2k 1 |
, |
k 0,1,..., n |
||||||||||||||
k |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2n 2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x |
|
|
|
a b |
t |
|
b a |
|
|
||||||||||||||
k |
|
|
|
k |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
n 1 |
|
Tn 1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2 |
n |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
x |
|
Tn |
|
|
|
|
|
|
|
|
|||||||||
T |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
n |
|
|
|
|
2n 1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9 | С т р а н и ц а
