Лекция № 10.
Итерационный процесс
С чебышевским набором параметров.
Многочлены Чебышёва.
Имели дело больше со стационарными процессами:
Многочлены Чебышёва определяются:
Свойство 1.
–чётная функция.
–нечётная функция.
Свойство 2.
Свойство 3.
Свойство 4.
Нули многочленов
на 
:
Свойство 5.
Экстремумы многочлена Чебышева.
Графики монотонны:
Рассмотрим нормировку:
Теорема 1.
Среди всех
многочленов степени n
со старшим коэффициентом 
наименее уклоняющимся от нуля является
многочлен 
,
т. е.
Предположим, что
не удовлетворяет условиям теоремы.
Рассмотрим точки
экстремума 
.
будет совпадать
с максимальным значением 
.
Точек экстремума
должно быть n
корней.
Это противоречит основной теореме Гаусса.
Утверждение 1.
Пусть 
,
тогда в качестве 
.
Равенство достигается, если 
.
Утверждение 2.
–максимальное
собственное число.
Вспомогательная задача.
многочлен степени
n.
Корни 
Далее будем
обозначать 
.
Чебышёвский процесс для вычисления решения системы.
Для решения задачи
минимакса примем в качестве параметра
множество нулей многочлена Чебышева
на отрезке 
.
Воспользуемся многочленом 
,
обладающим свойством 
и построим этот многочлен.
Теорема 2.
Пусть 
,
тогда рассматривая итерационный процесс
следует выбрать итерационный параметр
следующим образом:
При этом если число итераций n фиксировано, то достигается минимум:
–определено выше.
Замечание.
Особенность
многочлена Чебышева в том, что фиксируется
число итераций заранее и 
.
Замечание.
Так как при
построении итерационных процессов 
,
то выбор числа итераций 
.
Замечание.
–решение с заданной
точностью. Число n
удваивают (в этом случае) не производят
вычисление ещё раз.
Замечание.
Существуют такие
наборы, как, например, 
,
которые обеспечивают устойчивость
итерационных процессов.
Лекция № 11.
ИССЛЕДОВАНИЕ
СКОРОСТИ СХОДИМОСТИ
ИТЕРАЦИОННЫХ МЕТОДОВ.
Основные определения.
–малое число, а
– достаточно большое число.
–число раз, в
которое требуется уменьшить исходную
погрешность.
Итерационные метод сходятся с геометрической скоростью сходимости.
–оценка числа
итераций.
Определение 1.
Скоростью сходимости
итерационного метода называется величина
S – матрица перехода.
Пример.
Метод простой итерации с оптимальным выбором параметра.
Чебышевский процесс.
Так как 
,
то 
при достаточно больших n
стремится к 1. Для оценки числа итераций
будем использовать:
Пример.
Метод Якоби.
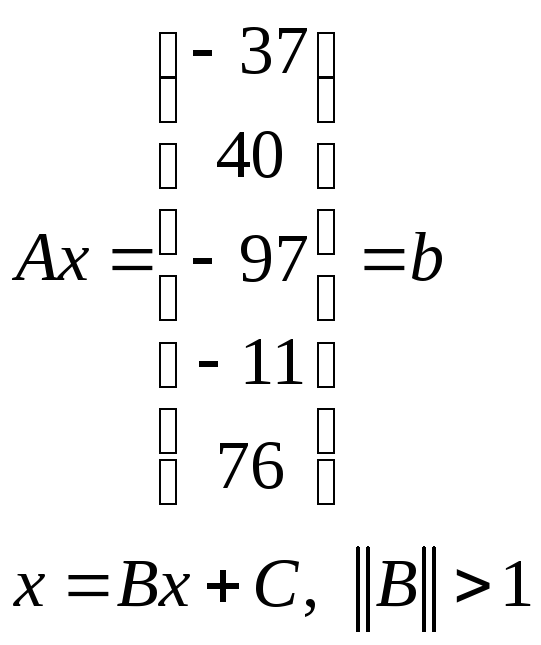
Метод разойдётся, так как матрица не обладает свойством диагонального преобладания.
МПИ с оптимальным выбором параметра.
Если спектр (разброс) большой, то матрица плохо обусловлена.
Метод Зейделя.
создаётся за 66
итераций.
Метод с Чебышёвский набором параметров.
Оценим сначала число итераций.
Недостатком данного метода является то, что необходимо знать собственные числа матрицы.
Другие итерационные методы.
Неявный итерационный процесс.
В неявных методах матрица B называется предобусловливателем.
Метод минимальных невязок.
Определение 1.
Невязкой называется
вектор 
.
Метод минимальных
невязок состоит в том, что параметр 
выбирается из условия 
при фиксированной норме невязки 
.
Условие
экстремума 
.
Теорема 1.
Метод минимальных поправок.
–поправка.
Лекция № 12.
ЧАСТИЧНАЯ
ПРОБЛЕМА СОБСТВЕННЫХ ЗНАЧЕНИЙ.
Вспомогательные сведения.
P – матрица перехода от исходного базиса к базису из собственных векторов.
Утверждение 1.
Пусть 
и 
– различные собственные числа, 
и 
– собственные вектора и матрица A
самосопряженная 
.
Тогда 
.
Пример.
Собственные числа растут и, вообще говоря, задача поиска собственных чисел большая проблема.
Исчерпывание корней.
Находим хотя бы
один корень, делим 
и опять применяем этот метод.
QR-алгоритм.
Рассмотрим матрицу:
Обозначим через
круг на комплексной плоскости с центром
в точке 
.
Определение 1.
Кругом Гержгорина
называется множество комплексной
плоскости 
.
Теорема 1.
Любые собственные значения матрицы A находятся в объединении кругов Гержгорина.
–максимальная
координата собственного вектора.
Следствие 1.
Если круг Гержгорина изолирован, то в нём находится одно собственное значение.
Следствие 2.
Если k кругов образуют замкнутую область, то там ровно k собственных значений матрицы A.
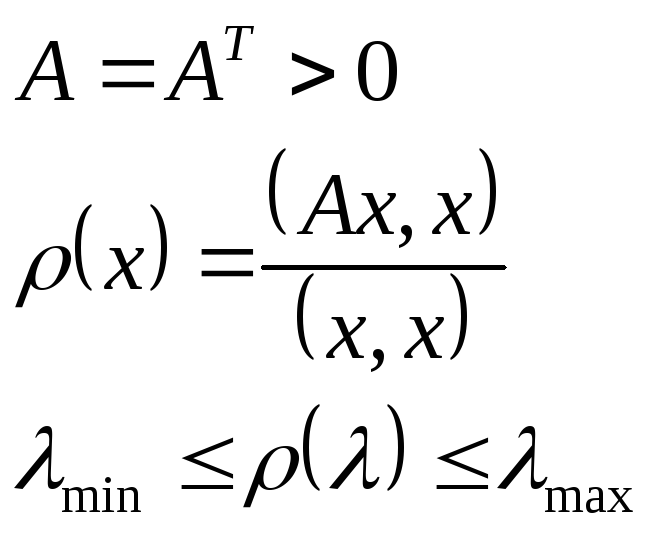
Для простоты пусть A – матрица простой структуры и пусть все собственные значения различны.
–максимальное
собственное значение.
Степенным методом называется метод (итерационный):
Теорема 2.
Пусть A
– матрица простой структуры и пусть 
– базис из собственных векторов. Тогда
и справедлива оценка:
Докажем только сходимость.
Модификация:
Пример.
