Обусловленность задачи решения слау.

Погрешность входного данного:

Теорема 1.

Пусть – точное решение системы , – решение системы . Тогда справедливы следующие оценки:





Определение 4.

Числом обусловленности матрицы А будем называть число .

Если , то матрица называется плохо обусловленной.

Пример.

Утверждение 1.

Пусть – точное решение системы , – решение системы . Тогда справедлива оценка .

Пусть – точное решение системы , – решение системы . Тогда справедлива оценка .

Пример.

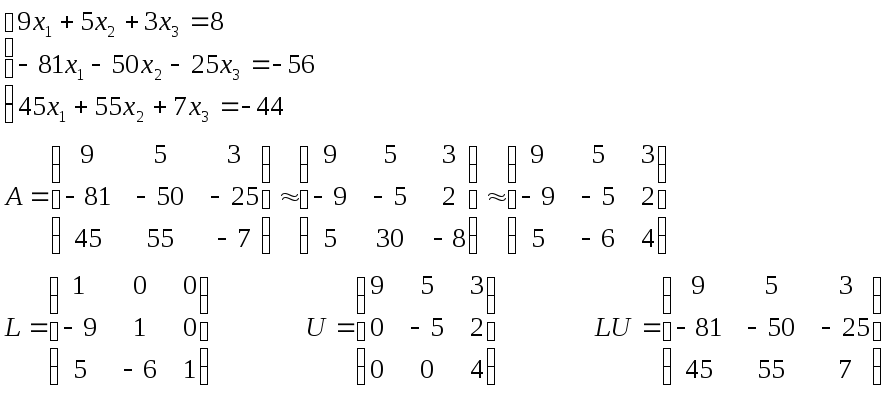
Решение системы методом Гаусса.

Обратный ход метода Гаусса:

Подсчитаем трудоёмкость метода Гаусса в общем случае.

1 шаг метода Гаусса.

Число алгоритмический действий:

Делений Умножений Вычитаний

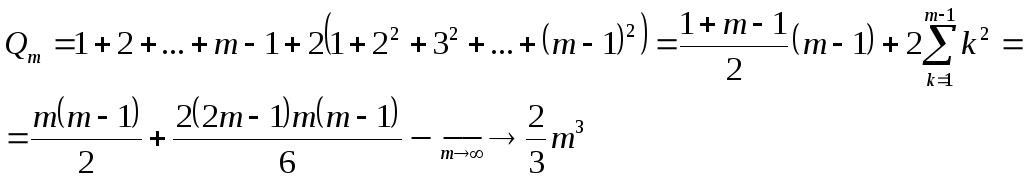
Лекция № 6. Решение слау прямыми методами. Метод Гаусса и его модификации.

Схема единственного деления.

1 шаг. Предполагаем, что – ведущий элемент 1-ого шага.

k шаг. – ведущий элемент k-ого шага.

Выписываем (m-1) шаг метода Гаусса.

арифметических действий.

Обратный ход.

Модификации метода Гаусса.

1. Схема частичного выбора метода Гаусса

(выбор максимального по модулю элемента по столбцу):

1 шаг. – максимальный по модулю элемент 1-ого столбца.

Меняем местами строки .

k шаг. – максимальный по модулю элемент k-ого столбца.

Меняем местами строки .

Преимущества схемы:

1. Нет деления на ноль.

2. –вычислительная устойчивость.

2. Метод полного выбора:

1 шаг. – максимальный по модулю элемент всей матрицы.

Меняем местами строки и столбцы .

k шаг. – максимальный по модулю элемент в подматрице порядка (m-k).

Меняем местами строки и столбцы .

Lu-разложение или матричная форма метода Гаусса.

Обычно стоит такая задача:

Выбираем правые части.

Рассмотрим элементарные матрицы:

Свойства элементарной матрицы:

1. 

2. 

3. Обратная матрица является той же матрицей, но с коэффициентами .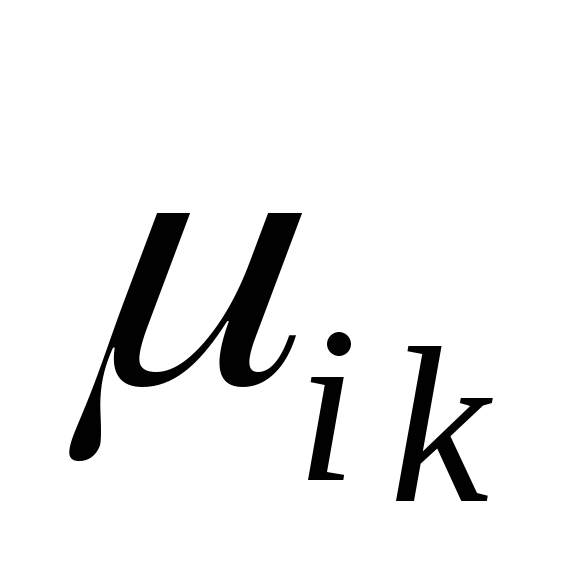

Найдём .

Пояснение.

Матричная схема метода Гаусса:

Пример.

Метод Холецкого (метод квадратных корней).

Определение 1.

Матрица A называется положительно определённой, если .

Критерий Сильвестра .

Определение 2.

Матрица A называется симметричной, если .

Достаточное условие положительной определённости в случае : если строковое диагональное преобладание, .

Пусть .

Число арифметических действий .

Пример.

Лекция № 7.

РЕШЕНИЕ СЛАУ.

Метод прогонки.

Определение 1.

Матрица разрежена, если содержит достаточное количество нулевых элементов.

Трёх диагональная система уравнений.

1 шаг.

2 шаг.

3 шаг.

Пример.

Теорема 1.

Достаточное условие применимости метода прогонки.

Пусть коэффициенты системы удовлетворяют следующим условиям:

Тогда , т. е. прогонка может быть доведена до конца и , т. е. прогонка устойчива.

По индукции.



Существуют различные способы прогонок:

1. Правая прогонка (классический способ).

2. Левая прогонка.

3. Более сложные формулы.