Теңбе-теңдiк ұғымын енгiзу туралы

Жаңа бағдарламаға сәйкес оқушылар теңбе-теңдiк ұғымымен алғаш рет 5-сыныпта танысады.

Алдымен әрiптi өрнек ұғымы айтылғаннан кейiн‚ әрiптi өрнектердi жазуда төмендегiдей ережелер мен шарттарды ескеру қажеттiгi айтылады:

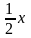1. Егер екi көбейткiштiң бiреуi сан болса, ол коэффициент деп аталып, ол әрiп көбейткiштiң алдына жазылады. Коэффициент пен әрiп көбейткiштiң арасына көбейту () таңбасын қоймауға да болады. Мысалы, 7х; 3у; ; 0,7у.

2. Әрiптi өрнектегi әрiп көбейткiштерiнiң арасына көбейту таңбасы қойылмайды. Мысалы, mn; 0,3ху; .

3. Құрамында әрiптерi бар бөлiндi, бөлшек түрiнде жазылады. Мысалы, .

4. Әрiптi өрнектегi амалдардың орындалуы кезiнде жақшаның алатын орны ерекше. Мысалы, 9-(a+b) өрнегi мен 9-а+b өрнегi бiрдей емес.

Өрнек бөлшекпен берiлген жағдайда, санды нөлге бөлуге болмайтындықтан, өрнектiң мағынасы болуы үшiн бөлшектiң бөлiмi нөлге тең болмауы шарт. Осы шарттың орындалуынан келiп, әрiптi өрнектегi әрiптердiң сан мәндерi ұғымы қалыптасады. Өрнектегi әрiптердiң сан мәндерi өзгерiп отыратындықтан, ондағы әрiптi айнымалы деп, әрпi бар өрнектi айнымалысы бар өрнек деп атайды. Мысалы. , өрнегiндегi х-тiң қабылдайтын мәндерi 0 санынан басқа барлық сандар; 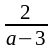өрнегi а үшiн а=3 санынан басқа барлық сандарды қабылдайды.

6-сыныпта теңбе-тең өрнек, теңбе-теңдiк және өрнектердi теңбе-тең түрлендiру ұғымдары енгiзiледi. Осы ұғымдардың нақтылы-индуктивтiк тәсiлге негiзделген енгiзу әдiстемесiн қарастырайық.

1. Теңбе-тең өрнектердi енгiзу мына сияқты тапсырманы қарастырудан басталады: 2х+3х² және 5х³ өрнектерiнiң мәндерiн х-тiң қандай да бiр мәндерiнде салыстырыңдар? Тапсырманы орындау үшiн мынадай кесте толтырылады:

X	2х+3х2	5х3
-0,4 -0,1 0 0,1 1 2	-0,32 -0,17 0 0,23 5 16	-0,32 -0,005 0 0,005 5 40

2х+3х² және 5х³ өрнектерiнiң мәндерi х-тiң кейбiр мәндерiнде бiрдей екендiгiн, ал басқа мәндерiнде әр түрлi екенiн байқауға болады.

1. Осылайша 7х³-х және 6х² өрнектерiнiң х=0; 1; - 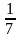; -1-ге тең болғандығы мәндерiнiң кестесi толтырылады:

X	7х3-х	6х2
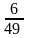
0 1 - -1	0 6 -6	0 6 6

Осы кестеге сүйене отырып жоғарыдағыдай қорытынды жасалды: 7х³-х және 6х² өрнектерiнiң мәндерi х-тiң барлық мәндерiнде тең емес.

3. 5(у+3) және 5у+15 өрнектерiн қарастырайық.

Айталық у=0; 1; -5; 4 болсын. Тiкелей есептеу арқылы у-тiң көрсетiлген мәндерiнде берiлген екi өрнек өзара тең екендiгiне көз жеткiзуге болады. Бұлар у-тiң басқа мәндерiнде тең бола ма? Осы сұраққа есептеу жұмыстарын жүргiзбей-ақ жауап беруге болады. Кез келген рационал сандар үшiн көбейтудiң үлестiрiмдiлiк заңы орындалатыны белгiлi, сондықтан 5(у+3) және 5у+15 өрнектерiнiң сәйкес мәндерi тең болады. Мұндай өрнектер теңбе-тең өрнектер деп аталады.

4. Теңбе-тең өрнектер ұғымының анықтамасы берiледi: «Егер айнымалының кез келген мәндерiнде екi өрнектiң мәндерi тең болатын болса, онда бұл өрнектердi теңбе-тең өрнектер деп атайды».

5. Жоғарыдағы тұжырымдалған анықтаманы бекiту үшiн жаттығулар орындалады: 1) р+25 және 25+р өрнектерiнiң барлық сәйкес мәндерi нелiктен тең болады? 2) бiр (екi, үш) айнымалысы бар екi теңбе-тең өрнектердi жазыңдар; 3) с(c-3) және c²-3 өрнектерiнiң теңбе-тең емес екендiгiн дәлелдеңдер.

6. Теңбе-тең түрлендiру ұғымының анықтамасы берiледi.

Бір аналитикалық өрнекті онымен теңбе-тең, бірақ формасы жағынан бсқаша өрнекпен алмастыру теңбе-тең түрлендіру деп аталады.

Өрнектi онымен теңбе-тең, берілгеніне қарағанда қарапайым өрнекпен алмастыру өрнектi ықшамдау делiнедi. Ықшамдағанға дейiнгi өрнек ықшамдағаннан кейiнгi өрнекпен теңбе-тең өрнек болды.

I. (4х+5)-3х+2=(4x-3x)+5+2=x+7. Сонда (4х+5)-3х+2 өрнегi мен х+7 өрнегi теңбе-тең өрнектер себебi, мысалы‚ егер х=1,3 болса, (4х+5)-3х+2=(41,3+5)-31,3+2=(5,2+5)-3,9+2=8,3 және х+7=1,3+7=8,3.

II. 5,2х23=(5,223)х=31,2х. Көбейту амалының ауыстырымдылық, терiмдiлiк қасиетiн пайдаланып ықшамдалды.