Жай бөлшек ұғымын енгізу

«Бөлшек сандар» тақырыбындағы ең негiзгi ұғым жай бөлшек болып табылады. Ол сипаттамалық түрде былай енгiзiледi: теңдей етiп 4-ке бөлiнген алманың суретi қарастырылады. Олардың бiреуi бiр тәрелкеге, ал қалған үшеуi басқа тәрелкеге салынады және былай дейдi: «Бiрiншi тәрелкеде алманың төрттен бiр бөлiгi, ал екiншiсiнде алманың төрттен үш бөлiгi жатыр». Мұны былай жазады: «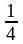 алма, 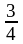алма». Бұдан кейiн мұндай және сандарының жай бөлшектер деп аталатыны хабарланады. бөлшегiнде 3 саны бөлшектiң алымы, ал 4 саны оның бөлiмi деп аталады. Бөлшектiң бөлiмi заттың (нәрсенiң) теңдей етiп қанша бөлiкке бөлiнгенiн, ал алымы сондай бөлiктен қаншасы алынғандығын көрсетедi. Алымын бөлшек сызығының үстiне, ал бөлiмiн оның астына жазады. Осындай түсiндiрулер басқа да мысалдар арқылы қайталанады. Алманың орнына теңдей етiп, төртке (сегiзге, алтыға, он екiге) бөлiнген дөңгелектi, (кесiндiнi, тiктөртбұрышты, квадратты) алуға болады.

Осы баяндауға сәйкес жай бөлшектердi енгiзудiң әдiстемелiк схемасы мынадай болады:

1) қарастырылатын затты теңдей етiп бірнеше бөлікке, біздің жағдайымызда 4 бөлiкке бөлу;

2) «төрттен бiр», «төрттен үш» терминдерiн хабарлау;

3) , жазуларын енгiзу;

4) «жай бөлшек», «бөлшектiң алымы», «бөлшектiң бөлiмi» терминдерi ненi көрсететiнiн айту;

5) бөлшектiң басқа мысалдарын келтiру, оларды оқу және жазу.

Бөлшек сандарды оқыту әдiстемесiнiң аса маңызды элементi жаңа сандарды енгiзу қажеттiлiгiне оқушылардың көзiн жеткiзу болып табылады. Оқушыларды сендiрудiң бiр жолы санның үлестерiн жазуда мұндай бөлшектердiң аса пайдалы екендiгiн түсiндiру. Бөлшек сандарды енгiзу қажеттiгiн оқушыларға былай түсiндiруге болады: Натурал сандар жиынында 2 саны 3 санына бөлiнбейдi. Бiрақ натурал сандарды бөлу амалы бөлшек сандар арқылы әрқашан орындалады. Натурал сандар жиыны бөлшектермен толықтырылады. 2-нi 3-ке бөлу амалын қарастырайық. 2 алманы 3 оқушыға тең бөлу қажет болсын. Мұны қалай орындауға болады? Әрбiр алманы теңдей етiп 3 бөлiкке бөлемiз. Сонда мұндай бөлiктiң бiрi бөлшегi арқылы өрнектеледi. Егер әрбiр оқушыға осыны екi бөлiктен беретiн болса, онда 2 алма 3 оқушыға теңдей етiп бөлiнген болады. Бiр алманың екi бөлiгi бөлшегi арқылы өрнектеледi. Олай болса, әрбiр оқушы алманың бөлiгiн алады, яғни 2:3= . Мынадай қорытынды жасалынады: ендi 2 натурал санын 3 натурал санына бөлуге болады, бөлу нәтижесiнде натурал сан емес, бөлшек сан шығады.

Ондық бөлшек ұғымын енгізу

Бөлiмдерi 10, 100, 1000 т.с.с. болатын бөлшектердi бөлiмсiз жазуға болады. Ол үшiн алдымен бөлшектiң бүтiн бөлiгiн, сонан соң үтiр қойып, алымын жазады.

Мысалы, .

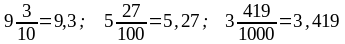Осындай жеке-жеке жағдайларды қарастыратын ой қорытудың индуктивтiк тәсiлi пайдаланылып, ондық бөлшектiң жазылуы, оқылуы (тоғыз бүтiн оннан үш, бес бүтiн жүзден жиырма жетi, т.б.) үйретiледi.

Дұрыс бөлшектi ондық бөлшек түрiнде жазғанда бөлшектiң бөлiмiнде неше нөл болса, ондық бөлшекте үтiрден кейiн сонша цифр болуы қажеттiгi түсiндiрiледi.

Мысалы, .

Ондық бөлшектiң соңындағы нөлдi алып тастағаннан немесе тiркеп жазғаннан оның мәнi өзгермейтiндiгi айтылады.

Мысалы, 2,31=2,310=2‚3100.

7,189 ондық бөлшегiнің бөлшек бөлігінде 1 ондық үлес, 8 жүздiк үлес, 9 мыңдық үлес бар.

Бөлiмi тек қана 2 және 5 сандарына еселi болатын жай бөлшектердi ондық бөлшектерге айналдыруға болатынына тоқталып, мысалдар келтiрiледi.

Оқушыларға проценттi ондық бөлшек түрiнде жазып көрсетiп, 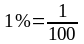болатындығы айтылады.

.
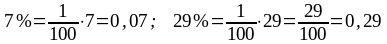