5.Қисық сызықты трапецияның ауданы туралы теореманы дәлелде.

Теореманың дәлелдемесiн үш бөлiкке бөлген тиiмдi.

I. S(х) функциясын енгiземiз. кесiндiсiнде анықталған х аргументiне байланысты қисық сызықты трапецияның ауданын өрнектейтiн S(х) функциясын қарастырайық. х аргументiне 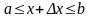болатындай етiп, x өсiмшесiн берейiк. Сонда S(х) функциясының х нүктесiндегi өсiмшесi болады (x –тi оң таңбалы деп қарастырамыз).

II. f(х) функциясы үшiн алғашқы функция S(х) болатынын көрсетейiк: барлық үшiн 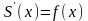. Туындының анықтамасына сәйкес: . S(х) – табаны х –ке тең болатын қисық сызықты трапецияның ауданы болатындықтан, оны табаны х-ке тең болатын, ал биiктiгi нүктесiндегi функцияның мәнif(с)-ға тең болатын тiктөртбұрыштың ауданымен алмастыруға болады: . Сонда

.

Мұнда с нүктесi х пен х+х аралығында жатқан нүкте болғандықтан, -да, , ал 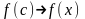, сондықтан 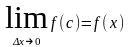. Бұл айтылған пайымдауларды бiр ғана қатар түрiнде былайша жазуға болады:

.

Сөйтiп, .

III. Нәтиженi қорытындылайық. Бiз S(х) функциясының кесiндiсiнде f(x) функциясы үшiн алғашқы функция болатындығын дәлелдедiк. Ал есептiң шарты бойынша F(x) осы кесiндiсiндегi f(x) функциясы үшiн де алғашқы функция болып табылады. Демек, S(х) пен F(x) функцияларының бiр-бiрiнен айырмашылығы тек тұрақты шама С–да ғана болады:

. (1)

x= болғанда (1) мынадай түрге келедi: 0=F( )+С, бұдан С=-F( ).

x=bболғанда (1) мына түрде жазылады:

S=S(b)=F(b)+С=F(b)-F( ).

Сонымен, S=F(b)-F( ).

6.Интеграл ұғымын енгізудің әдістемелік схемасы қандай болуы мүмкін?

Интеграл ұғымын енгiзу ең негiзгi қадам болып табылады. Интеграл ұғымын енгiзудiң бiр әдiстемелiк схемасы мынадай:

1) лайықты есептер келтiру; 2) интегралдың анықтамасын тұжырымдау.

Интеграл ұғымын оған келтiретiн дайындық есептерiн қарастырудан бастаған тиiмдi.

7.Интеграл ұғымына келтірілетін қандай дайындық есептерң шығарылады?

Интеграл ұғымын оған келтiретiн дайындық есептерiн қарастырудан бастаған тиiмдi.

1-есеп. кесiндiсiнде үздiксiз және терiс емес 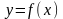функциясы берiлciн. Алғашқы функция ұғымына байланыссыз осы функциямен x=a және x=b түзулерiмен шектелген қисық сызықты трапецияның ауданы S-тi табудың жаңа тәсiлiн көрсетiңдер.

Берiлген есептi шешудi екi кезеңге бөлуге болады.

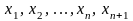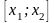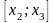1.Сатылы фигураны құрып, оның ауданын есептеу. Ол үшiн кесiндiсiн теңдей етiп n бөлiкке бөлемiз. Айталық х – осындай кесiндiнiң әрбiреуiнiң ұзындығы болсын. Бөлу нүктелерiн , мұндағы деп белгiлеймiз. кесiндiсiн табаны етiп, биiктiгif(x₁) болатын, ал кесiндiсiнде – биiктiгif(x₂) болатын тiктөртбұрыш саламыз. Дәл осы сияқты қалған кесiндiлерде де тiктөртбұрыштар саламыз. Сонда бұл тiктөртбұрыштардың барлығы бiрiгiп, “сатылы” фигураны құрады және оның ауданы мынаған тең болады:

.

2.Қисық сызықты трапецияның ауданы S-тi S_n арқылы өрнектеу. Ендi кесiндiсiн өте “ұсақ” бөлiктерге бөлудi қарастырайық. Ол үшiн жоғарыдағы тәсiлмен сатылы фигура құрамыз. Сондағы шыққан суреттердi салыстыру арқылы х неғұрлым аз болған сайын, яғни n үлкен болған сайын, S_n шамасы S–тен соғұрлым аз өзгеретiнiн көремiз. Сондықтан қисық сызықты трапецияның ауданы S_n-нiң шегi деп қарастыруға болады. Математикада бұл деректiң шынында да орындалатындығы дәлелденедi. Сонымен,

.

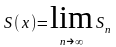Шешiмi осындай 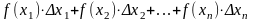қосындының шегiн табуға келiп тiрелетiн тағы бiр есептi қарастырамыз.

2-есеп. Айталық, материалдық нүкте кесiндiсiнде түзу сызықпен белгiлi бiр ( кесiндiсiндегi үздiксiз функция) лездiк жылдамдықпен қозғалсын. Осы материалдық нүктенiң Т₁ мен Т₂ уақыт аралығындағы жүрген жолын табу қажет болсын.

Қарапайым жағдайда, лездiк жылдамдық тұрақты шама болғанда, дененiң жүрген жолы оның жылдамдығы мен уақытының көбейтiндiсiне тең болады. Жалпы жағдайда, лездiк жылдамдық тұрақты болмаған кезде, бұл есептi былайша шешедi.

1. кесiндiсiн бөлу нүктелерi арқылы ұзындықтары бiрдей 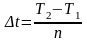болатын n бөлiкке (кесiндiге) бөлемiз. Содан кейiн

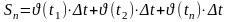қосындысын құрамыз.

2. S жолын S_n арқылы өрнектеймiз: S_n-дегi әрбiр қосылғыш дененiң сәйкес уақыты аралығында жүрген жолын жуық шамада көрсетедi.

Бұл жуықтаудың нәтижесi t неғұрлым аз, яғни, n бөлiк неғұрлым үлкен болған сайын, соғұрлым дәлiрек болатындығы айқын. Сондықтан, дененiң уақыт аралығында жүрген жолы шегi арқылы анықталады.