§8.Частные решения систем линейных дифференциальных уравнений с постоянными коэффициентами для правых частей специального вида.

(8.1)

Принцип суперпозиций.

Утверждение.

- является решением системы (8.1).

Доказательство.

Чтд

(8.1)

Умножим на :

Подсистема с номером :

экспонента исчезает, но степень оставшегося многочлена нарастает отдо.

, если

, если.- максимальный из размеров жордановой клетки, соответствующей.

Получен общий вид. Для поиска коэффициентов используем метод неопределенных коэффициентов.

При этом учли, что:

§9.Линейное дифференциальное уравнение порядка m с постоянными коэффициентами.

(9.1)

(9.1)

(9.2)

Лекция №15.

,

Однородное уравнение

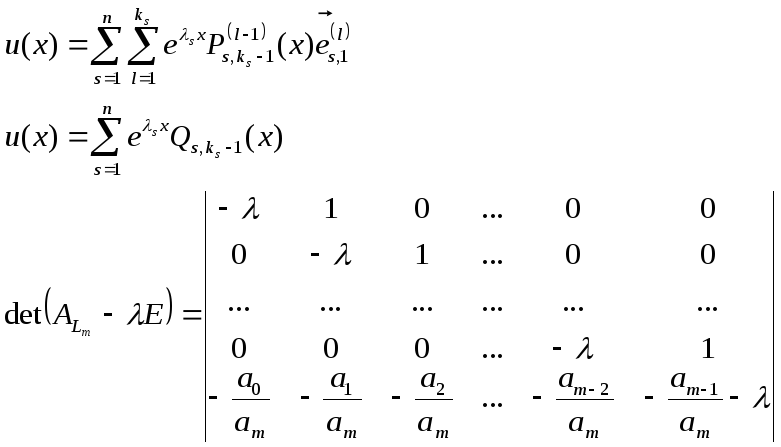
Раскроем определитель по последней строке

Умножим на :

Найдем собственные числа и их кратность(= числу жордановых клеток).

Число жордановых клеток = любомусоответствует одна жорданова клетка.

первая компонента собственного вектора

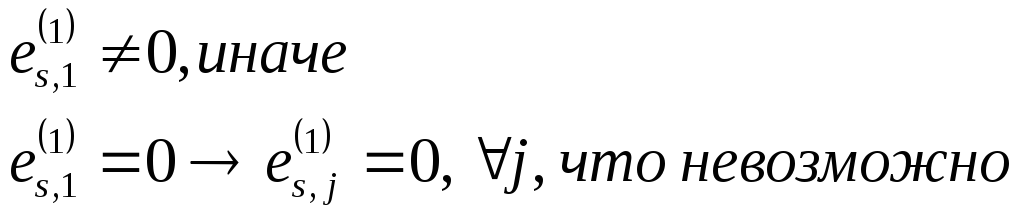
Зададимся произвольным набором коэффициентов с

Итак,

Частное решение дифференциального уравнения для правых частей специального вида.

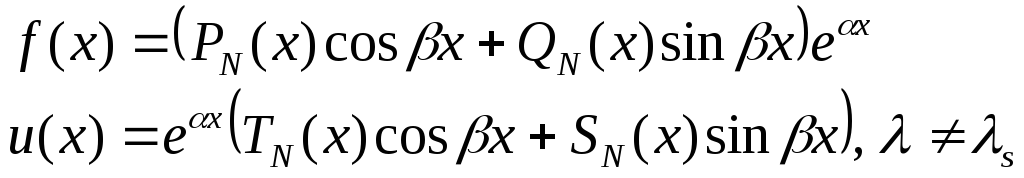
кратность корня.

Теория устойчивости

§1.Понятие об устойчивости по Ляпунову и асимптотической устойчивости.

(1.1)

(1.2)

Будем полагать, что существует, единственно и определено для всех.

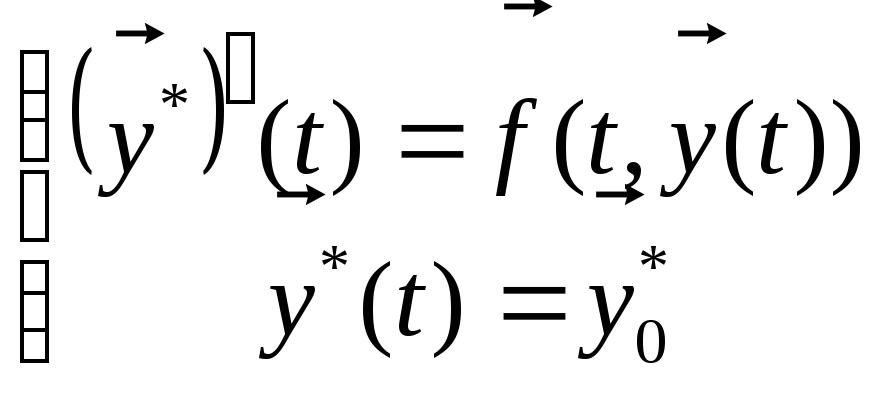(1.3)

- возмущенное начальное значение.

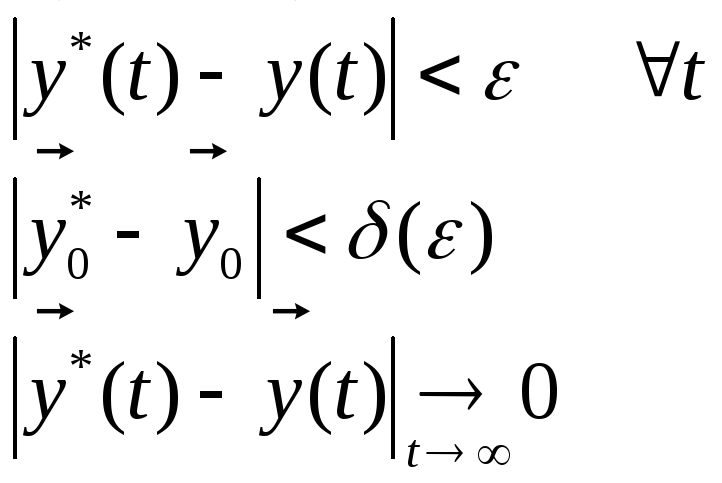
Определение.

Решение задачи (1.1), (1.2) называется устойчивым по Ляпунову, если

Определение.

Решение задачи (1.1), (1.2) называется асимптотически устойчивым, если оно устойчиво по Ляпунову и

Лекция №16.

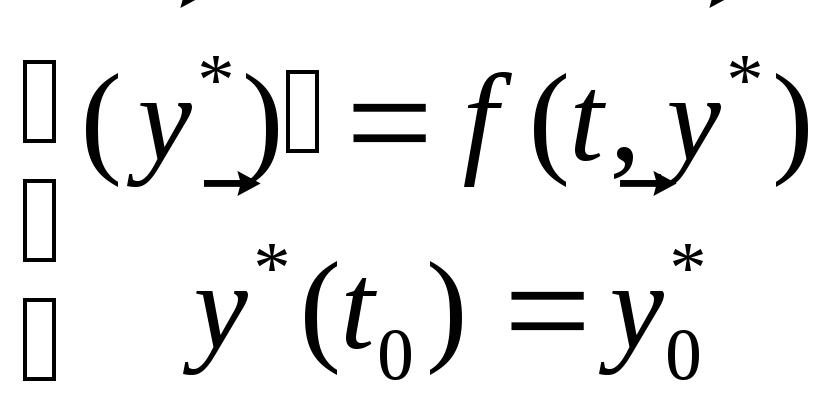
Пример.

Проведем исследование на устойчивость

- некоторое комплексное число.

Вычтем:

,

Итог – устойчивость по Ляпунову.

Если , то устойчивости по Ляпунову нет.

есть асимптотическая устойчивость.

нет асимптотической устойчивости.

Вычтем из (1.3) (1.1):

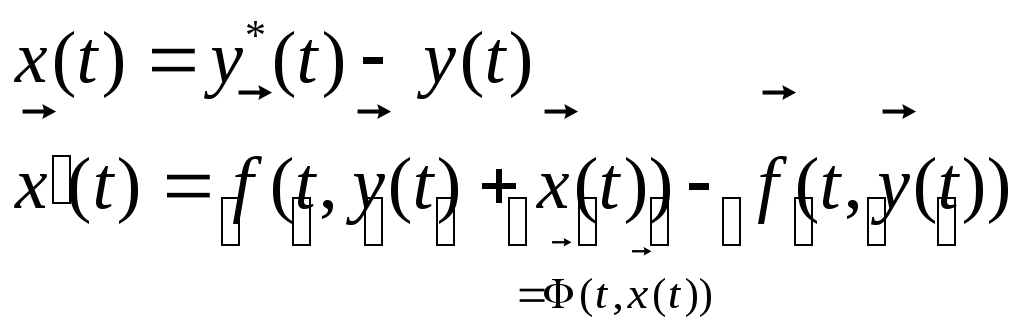
Определение.

Точка покоя системы (1.5) называется устойчивой по Ляпунову, если

Определение.

Точка покоя системы (1.5) называется асимптотически устойчивой, если она устойчива по Ляпунову и

Неустойчивость:

Ограничение, накладываемое на правую часть системы (1.5):

§2.Устойчивость систем линейных дифференциальных уравнений с постоянными коэффициентами.

А– матрицы с постоянными элементами.

Теорема 2.1

Точка покоя системы (2.3) устойчива по Ляпунову тогда и только тогда, когда справедливо следующее свойство:

(А)

Доказательство.

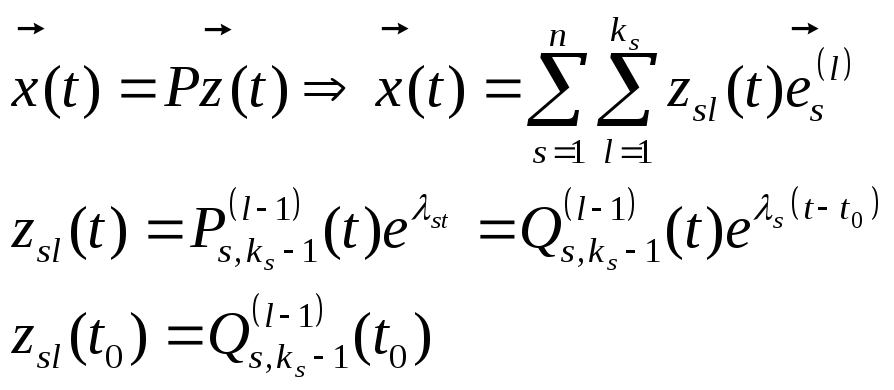
Разложение Тейлора:

Предположим, что (А) выполняется:

• Если

• Если

(А)

Точка покоя устойчива по Ляпунову

Обратно:

от противного, пусть точка покоя устойчива и не выполнено свойство (А), т. е.

• Либо

• Либо

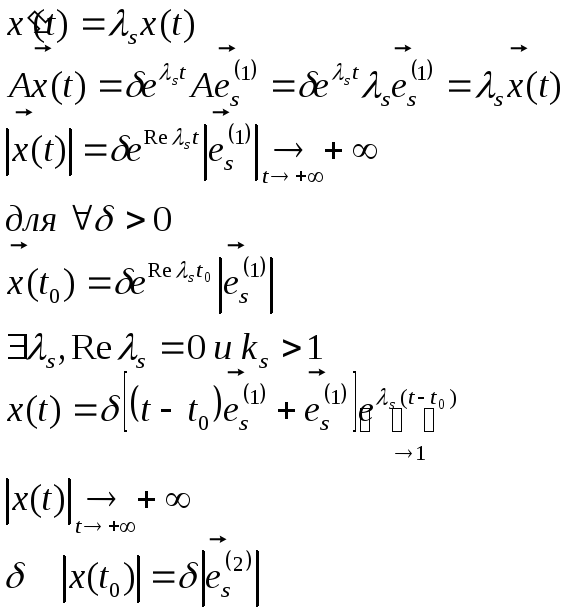
В обоих случаях устойчивости нет. Противоречие.

Лекция №17.

,А– матрица с постоянными коэффициентами.

Теорема 2.2

Для того, чтобы точка покоя была асимптотически устойчивой, необходимо и достаточно, чтобы

Доказательство.

устойчивость по Ляпунову.

Обратно:

Асимптотическая устойчивость. Пусть

§3.Простейшие типы точек покоя

(пропущено. См. конспект)

Лекция №18.