Лекции по дифференциальным уравнениям
3 семестр
Лектор Амосов Андрей Авенирович
Лекция № 1. ВВЕДЕНИЕ. ОБЩИЕ ПОЛОЖЕНИЯ.
Определение 1.
Обыкновенным
дифференциальным уравнением (ОДУ) n-ого
порядка называется соотношение вида
между независимой переменной
,
искомой функцией
и её производными
.
–искомая функция.
Определение 2.
Решение ДУ (1) –
функция
,
подстановка которой и её производных,
обращает его в тождество.
График решений ДУ называется интегральной кривой.
Пример.
1.
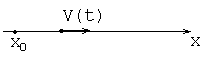
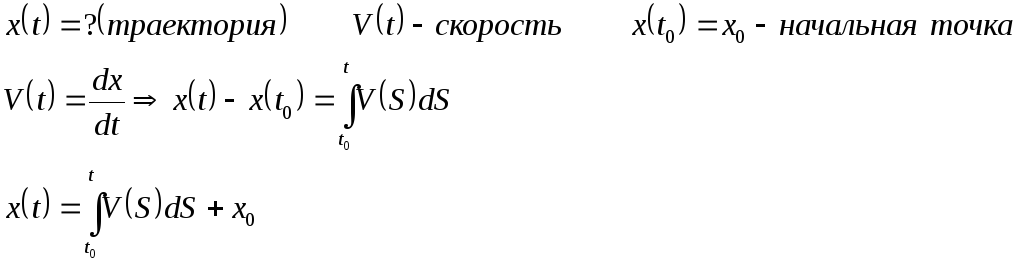
2.
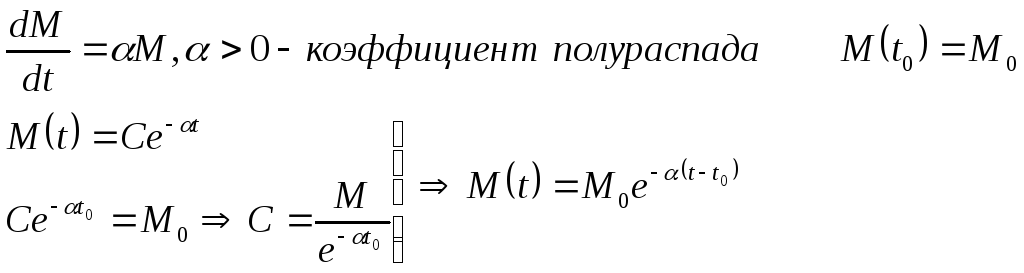
Определение 3.
Общее решение ДУ – множество всех его решений
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА.
§1. ДУ I порядка, разрешенные относительно производной.
задана и непрерывна
в некоторой области G
плоскости Оxy
.
Определение 4.
Пусть
,
тогда промежутком
.
Определение 5.
Функция
,
определённая на
,
называется решением ДУ (1.1), если:
Замечание.
Область определения решений – связанное множество.
Пример.
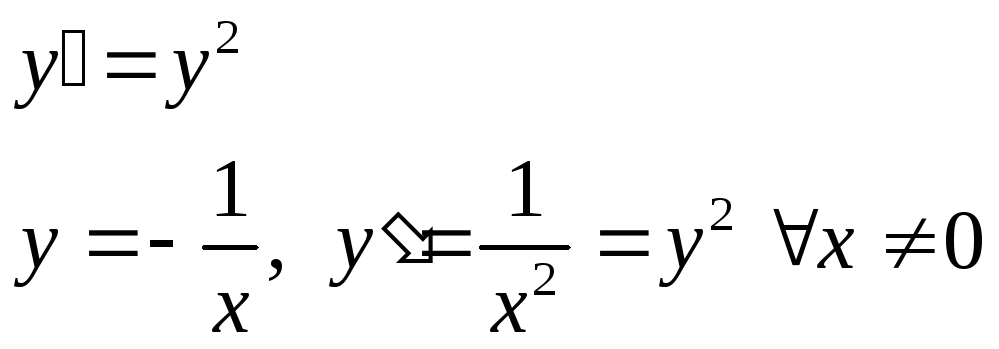
Понятие о поле направления.
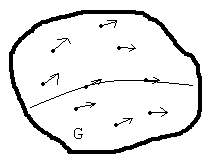
Метод изоклины.
Изоклина – кривая
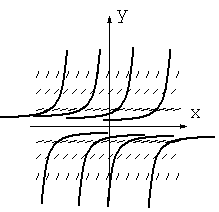
Пример.
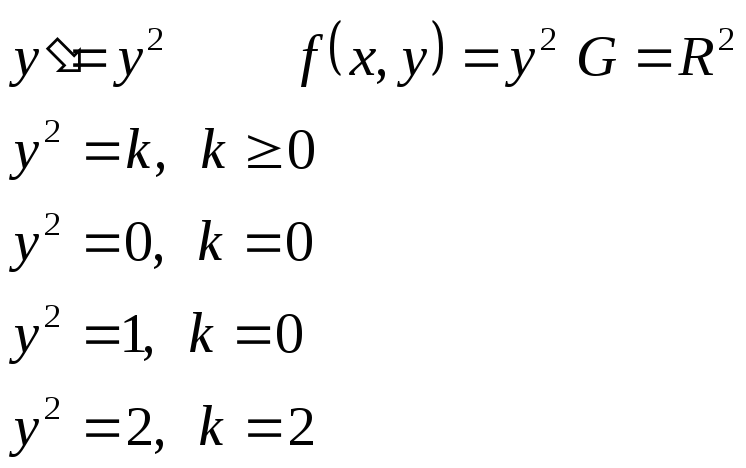
§1. ДУ I порядка в симметрической форме.
(2.1)
Лекция №2
Если в некоторой окрестности точки функция
,
то из
.
(2.2)
Здесь функция
зависит
от
и при подстановке в уравнение (2.1) получаем
верное тождество.
А если
,
то
.
(2.3)
В этом случае
функция
зависит от
.
Уравнения в полных дифференциалах.
Определение.
Уравнение (2.1) называется уравнение в
полных дифференциалах, если существует
функция
для которой левая часть уравнения (2.1)
является первым дифференциалом:
.
Это будет тогда,
когда
,
а
.
Пример.
.
Теорема 2.1
Пусть (2.1) – уравнение в полных дифференциалах. Тогда общий интеграл дифференциального уравнения (2.1) имеет вид:
,
(2.4)
где
– произвольная постоянная.
Доказательство.
Пусть
в окрестности
.
Пусть также
– решение дифференциального уравнения
(2.1), т.е. уравнение (2.2).
.
Обратно.
Пусть некоторая
гладкая функция
удовлетворяет уравнению (2.4) для
=>
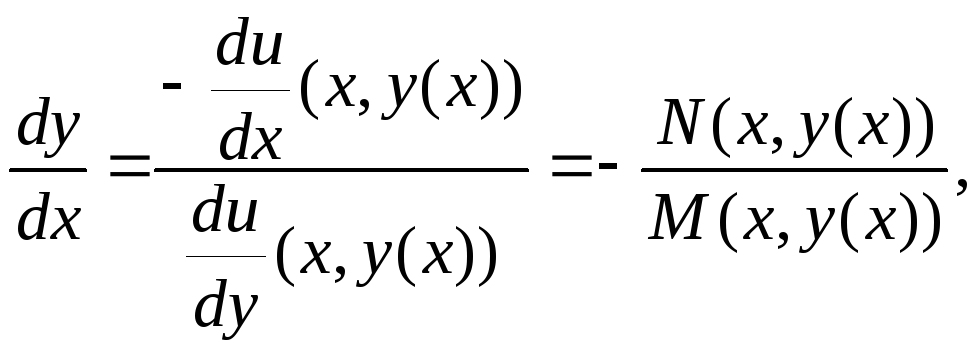
(2.2) =>
является решением (2.1).
Случай, когда
доказывается аналогично.
Теорема 2.2
Пусть
непрерывны в окрестности некоторой
точки
.
Для того, чтобы
уравнение (2.1) было уравнением в полных
дифференциалах необходимо и достаточно,
чтобы
.
Доказательство.
Пусть (2.1) является
уравнением в полных дифференциалах и
существует функция
.
Тогда
;
.
Т.к.
и
непрерывны, то
=>
Обратно.
Пусть
.
Тогда положим
.
.
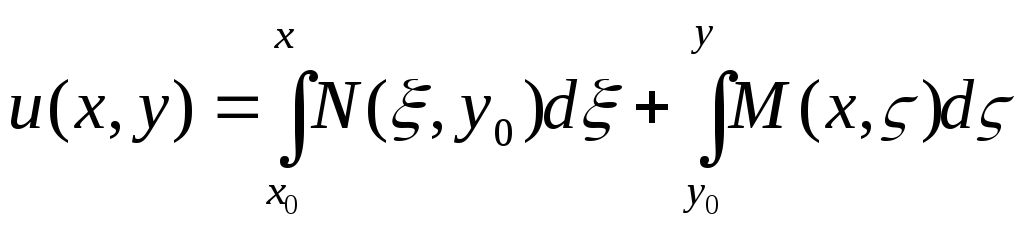Функции
и
непрерывны, значит
непрерывно дифференцируема и
.
Замечание.
Иногда дифференциальные
уравнения (2.1) не являются уравнениями
в полных дифференциалах. Однако, найдется
функция
такая, что при умножении на (2.1)
Если это так, тогда
– интегрирующий множитель.