Добавил:

Tushkan Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Дифференциальные уравнения

Файл:

Лекции (2)

.pdf

Скачиваний:

Добавлен:

28.06.2014

Размер:

1.32 Mб

Скачать

☆

1 / 81 2 3 4 5 6 7 8 > Следующая >>>

МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ (ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

Лекции

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

4 семестр

Лектор Амосов Андрей Авенирович

Москва, 2009/2010

		Содержание
	КРАЕВЫЕ ЗАДАЧИ.
Лекция № 1.	Краевые задачи. Постановки краевых задач ................................									3
	Задачи с однородными краевыми условиями. Сведение задач с
	неоднородными условиями к задачам с однородными краевыми
	условиями .........................................................................................									7
Лекция № 2.	Некоторые свойства решений уравнения L[U]=0 ........................									8
	Неоднородные краевые задачи. Функции Грина								.......................	11
Лекция № 3.	Неоднородные краевые задачи. Функции Грина								.......................	12
	Физический смысл функции Грина .............................................									15
	Принцип максимума. Теоремы сравнения. Априорная оценка
	решения первой краевой задачи ..................................................									16
Лекция № 4.	Задача Штурма-Лиувилля ............................................................									18
	Матричная экспонента. Формула Коши .....................................									21
	Разрешимость двухточечной краевой задачи для системы
	линейных дифференциальных уравнений ..................................									23
	ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ.
Лекция № 5.	Введение. Задача о Брахистохроне. Задача Дидоны ..................									25
	Функционалы,	сильный			и	слабый			дифференциалы.
	Необходимое условие экстремума					..............................................				26
	Дифференцируемость простейшего функционала вариационного
	исчисления .....................................................................................									31
Лекция № 6.	Основная лемма вариационного исчисления. Лемма Дюбуа-
	Реймона ..........................................................................................									33
	Простейшая задача вариационного исчисления (задача с
	закреплёнными концами). Уравнение Эйлера ...........................									35
Лекция № 7.	Простейшие случаи интегрируемости ур-я Эйлера ...................									37
Лекция № 8.	Задача со свободными концами ...................................................									41
	Задача с подвижными концами. Условие трансверсальности .. 43
	Задача с двумя подвижными концами ........................................									45
Лекция № 9.	Функционал Больца ......................................................................									46
			b



	Функционалы вида J y			F x, y, y		dx .........................................				47
			a
			b
							m
	Функционалы вида J y F x, y, y , y ,..., y							dx ...........................		49
			a
Лекция № 10. Минимизация выпуклого функционала ......................................										50
Лекция № 11.	Вторая Вариация функционала. Необходимое									условие
	экстремума в терминах второй вариации. Условие Лежандра . 54
	Классические достаточные условия экстремума								.......................	56
Лекция № 12. Усиленное условие Якоби ............................................................										57
Лекция № 13.	.......................................................................................................... 61
									1 \| С т р а н и ц а

Лекция № 14.	Изопериметрические задачи. Абстрактная изопериметрическая
	задача ..............................................................................................	63
Лекция № 15.	Классическая изопериметрическая задача ..................................	65
	Вариационные задачи на условный экстремум при наличии
	голономных и не голономных условий связи ............................	67
Лекция № 16.	Понятие о неголономных связях .................................................	69
	Задача о геодезических линиях ....................................................	70
	Геодезические линии на сфере ....................................................	71
Экзаменационная программа .................................................................................		72

2 | С т р а н и ц а

Лекция № 1.

КРАЕВЫЕ ЗАДАЧИ. ПОСТАНОВКИ КРАЕВЫХ ЗАДАЧ.

Рассмотрим задачу Коши, которая удовлетворяет некоторому ДУ и начальному условию.

Начальная задача

Поставим дополнительные условия.

Многоточечная задача

Наиболее распространённая задача – задача с двумя дополнительными условиям (точками a и b).

Краевая (граничная) задача

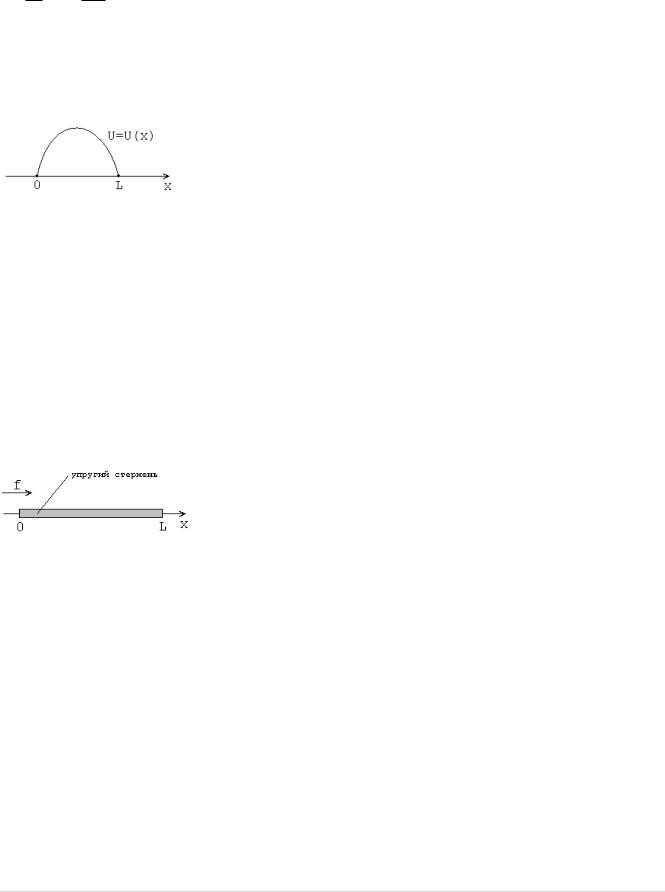
Пример 1.1.

Задача о статическом равновесии упругого стержня.

f f x – сила, действующая на все точки стержня (например, инерции и т. п.)

Если закрепить левую и правую точки стержня U 0 0, U l 0 стержня описывается уравнением:

сила тяжести, сила

, тогда равновесие

	d		p x	dU	f x – уравнение статического равновесия стержня.
	dx		p x		f x – уравнение статического равновесия стержня.

				dx

		физический смысл
		напряжение
p x – коэффициент упругости стержня
1 x l

(1)

Из уравнения видно, что изменение напряжения вызвано действием силы.

Требуется найти решение уравнения (1), для которого выполнены два условия:
U 0 0	2
U l 0	3

3 | С т р а н и ц а

Определение 1.1.

Система из уравнения (1) и дополнительными условиями (2) и (3) называется краевой задачей.

	d	p x	dU	f x
		p x		f x

	dx		dx

U 0 0

U l 0

Решением краевой задачи будет некоторая функция

Можем поставить следующие условия:

U(0) U		0
U l U
	l

U x

Как вариант, может быть рассмотрена тепловая задача, тогда U U x – температура;

p(x) – коэффициент теплопроводности;

f f x – плотность теплового источника.

Пример 1.2.

Задача об установившихся гармонических колебаниях упругого стержня.

f	f x e	i t	– гармоническая сила;

	– частота колебаний;

U U x ei t – амплитуда колебаний. Уравнение описания процесса:

	d	p x	dU	2	x U f x
		p x		2	x U f x

	dx		dx		плотность
					плотность
					стержня

U 0 0			Граничные условия
			Граничные условия
U l 0

4 | С т р а н и ц а

Пример 1.3.

Задача о траектории.

t – время;

– координаты точек.

r0 , r1

Требуется за время						t	попасть из

	F
ma	F
	d	2			t
	d
a	dt		2	r
			2

Краевая задача для системы ДУ II


r0	в	r1 .

порядка:

r t

r ,

r t

Общий вид ДУ II

порядка:

a x U ''b x U 'c x U g x , a 0,

Поделим на a x :

U ''

b x

U '

c x

g x

a 0

a x

a,b,c

– гладкие функции.

p x e

Введём

Умножим уравнение на p x :

p x U '' p x

b x

U ' p x

c x

g x

p x

q x U f x

U p x

a x

q x

f x

Обозначим L[U ]	d	p x	dU	q x U дифференцирующий оператор.
Обозначим L[U ]		p x		q x U дифференцирующий оператор.

	dx		dx
В итоге, получили новый вид ДУ II порядка:
		L[U ] f x

Краевые условия:

1U ' 0 1U 0 12U ' l 2U l 2

(1.1)

(1.2)

(1.3)

2	2	0
1	1		(не могут обращаться в ноль одновременно)
2	2	0	(не могут обращаться в ноль одновременно)
2	2	0
2	2

(1.1), (1.2), (1.3) – краевая задача.

5 | С т р а н и ц а

Определение

Если 1 0

1.2.

, то краевое условие называется однородным краевым условием,

иначе – неоднородным. Варианты краевых условий:

1. 2. 3.

111

0 1

0, 1 0

0 U 0

U 0 U0

– краевое условие 1

рода.

ого

0 U' 0

' U ' 0 U0 ' – краевое условие 2

ого

рода.

U' 0

U 0

U ' 0 1U 0 1 – краевое условие 3

ого

рода

(общего вида).

L[U ] f x

U 0 U			0
			0
	U
U l	U	l
		l
L[U ] f x
					'
U ' 0 U				0	'
				0
				'
U ' l U				'
			l

1ая

2ая

краевая задача.

Физический вариант записи.
1. Краевое условие 2		ого	рода:
		ого
p 0 U '(0) ,	p x p		0
0		0	рода:
2. Краевое условие 3			рода:
	ого
p 0 U '(0) U 0		,	p x p	0
1	0		0

Определение 1.3.
Уравнение	вида	L[U ] 0 называется
L[U ] f x	– неоднородным уравнением

однородным уравнением II порядка, а II порядка.

Далее будем предполагать, что p, q, f C 0;l и

p x p	0
0

0;l

Определение 1.4.
Решением ДУ		L[U ] f x			называется функция
следующим условиям:
1.	U C1 0;l ;
2.	Функция	p x	dU	C1 0;l ;
2.	Функция	p x	dx	C1 0;l ;
			dx
3.	При подстановке в ДУ получаем тождество L[U

]

U x ,

x x

удовлетворяющая

0;l .

6 | С т р а н и ц а

ЗАДАЧИ С ОДНОРОДНЫМИ КРАЕВЫМИ УСЛОВИЯМИ. СВЕДЕНИЕ ЗАДАЧ С НЕОДНОРОДНЫМИ УСЛОВИЯМИ К ЗАДАЧАМ С ОДНОРОДНЫМИ КРАЕВЫМИ УСЛОВИЯМИ.

L[U ] f x

U ' 0 U 0			1
	1	1	1

U ' l U l			2
	2	2	2

V ' 0 V

Найдём V x .

Возьмём кубическую параболу V x

V ' l V

U 0 U

V x U0

Ul U0

линейная функция

l U

Обозначим

z U V , где U – искомая функция, V – найденная.

L[z] L[U ] L[V ]

f L[V ]

0 0

Задача с однородными граничными условиями.

1z' 0 1z

z' l

l 0

7 | С т р а н и ц а

Лекция № 2. НЕКОТОРЫЕ СВОЙСТВА РЕШЕНИЙ ОДНОРОДНОГО УРАВНЕНИЯ L[U]=0

L[U ]	d	p x	dU	q x U ,	p, q 0;l ,	p x p		0
							0

	dx		dx

Сведём ДУ 2-ого порядка к системе ДУ 1-ого порядка:

L[U ] 0

Определитель Вронского

W x

y x

z x

, y,

0;l

p x y' x

p x z' x

z C

W x p x W

x ,

y x

z x

y' x

z' x

Лемма 2.1.
Пусть функции y,	z являются решениями однородного уравнения
		L[U ] 0 ,	x 0;l
и удовлетворяет однородному граничному условию
		U ' 0 U 0 0
		1	1
		или
		U ' l U l 0
		2	2
Тогда эти функции y и z		линейно зависимы.

(2.1)

(2.2)

(2.3)

	W 0	y 0
	W 0	p 0 y' 0
		p 0 y' 0

z 0 p 0 z' 0

Если y и z	удовлетворяют условию (2.2), то
1y' 0 1 y 0 0

1 z' 0 1 z 0 0		Строки в определителе Вронского линейно зависимы
12 12 0

p 0 0

x : W 0 0 y, z линейно зависимы.
Аналогично, если y		и z удовлетворяют условию (2.3).

8 | С т р а н и ц а

Приложение 2.1. (Тождество Лагранжа)

Пусть

1	0;l
z C

p	dy	,
	dx

dz dx

C	0;l , тогда справедливо тождество Лагранжа
1
zL[ y] yL[z]		dW	на 0;l	(2.4)
zL[ y] yL[z]		dx	на 0;l	(2.4)
		dx

zL[ y] yL[z] z

qzy

qyz

dz dy

W x

dx dx

Следствие 2.1.

zL[ y] yL[z] dx W l

W 0 .

Справедлива формула Грина

Следствие 2.2.

Если y

z удовлетворяют одновременно граничным

zL[ y]

yL[z] dx 0 .

формула Грина принимает вид

p	dy dz	d		dz
p			py
	dx dx	dx		dx

условиям (2.2), (2.3), то

Следствие 2.3. Если функции

являются решениями однородного уравнения

L[U ]

, то

W x const

Из (2.4)

dW dx

0 W

const

Будем рассматривать уравнение L[U ] 0		, x 0;l
Типы краевых условий:
I. U 0 0; U l 0
II. U 0 0; p l U ' l 1U l 0
III. p 0 U ' 0	0U 0 0; U l 0
IV. p 0 U ' 0	0U 0 0; p l U ' l 1U l 0

(Эквивалентны 9 типам краевых условий)

0 , 1 0

Теорема 2.1.

Пусть U – решение однородного уравнения уравнениям граничных условий I, II, III

(2.1)

(2.1) удовлетворяет однородным или IV. Пусть дополнительно

	l	(*) в случае условий IV. Тогда U x 0 .
q x 0	и 02 12 p x dx 0	(*) в случае условий IV. Тогда U x 0 .
	0

9 | С т р а н и ц а

1 / 81 2 3 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете Дифференциальные уравнения

#
28.06.201437 Кб17Контрольная работа (варианты).docx
#
28.06.20142.08 Mб146Лекции (1).doc
#
28.06.20141.32 Mб94Лекции (2).pdf
#
28.06.201436.35 Кб17Экзаменационная программа (2010).doc
#
28.06.201473.31 Кб38Экзаменационная программа.pdf