§8.О гладкости решений дифференциального уравнения.

(8.1)

- решение, определенное на

на (8.2)

Теорема 8.1

Пусть - решение дифференциального уравнения (8.1), определенное на. Если, где, то.

Доказательство.

…

В итоге

Следствие.

Если правая часть дифференциального уравнения является бесконечно дифференцируемой, то решение тоже является бесконечно дифференцируемым.

§9.Дифференциальные уравнения первого порядка, не разрешенные относительно производных.

(9.1)

(9.2)

Пример 9.1.

Для задачи Коши добавим условие (одного уже не достаточно)

Пример 9.2

,

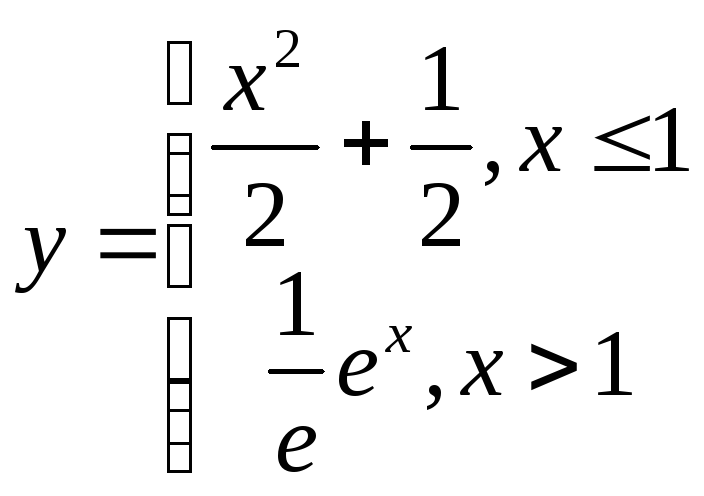
Методы решения.

1. 

2. метод введения параметра.

3. метод введения параметра.

Это равенство справедливо в силу инвариантности формы первого дифференциала.

Уравнение Лагранжа.

метод введения параметра.

Уравнение Клеро.

Частный случай уравнения Лагранжа. Но при решении методом ввода параметра возникает деление на ноль.

Лекция № 7.

(9.1)

(9.2)

(9.3)

(9.4)

Теорема 9.1.

Пусть задана и непрерывна в некоторой окрестноститочки. Пусть также,непрерывны в этой окрестности и выполняется условия:

1)

2)

Тогда существует решение дифференциального уравнения (9.1), определенное на отрезке , удовлетворяющее условиям (9.2), (9.3).

Если дополнительно , непрерывная в, то это решение единственно.

Доказательство.

По теореме о неявной функции при выполнении условий непрерывности и, где- непрерывная функция, заданная в некоторой окрестноститочкии такая, что,- единственная.

Из теоремы Пеано получаем, что существует решение, определенное на .

- непрерывная функция, следовательно выполняется условие Липшица по переменной . Значит решение единственно.

§10.Неравенство Гронуолла.

(10.1)

Теорема 10.1 (лемма Гронуолла)

Пусть , удовлетворяющая дифференциальному неравенству (10.1), где.

Тогда справедливо неравенство Гронуолла:

(10.2)

Доказательство.

Решение дифференциального неравенства оценивается сверху решением дифференциального уравнения.

Проинтегрируем от до(текущей точки):

Следствие 10.1

Пусть неотрицательная функция удовлетворяет неравенству

, где (10.3)

Тогда функция удовлетворяет неравенству Гронуолла (10.2).

Доказательство.

Фиксируем точку . Рассмотрим. Могут быть два варианта.

1) - очевидно, ведь правая часть неотрицательна.

2)

2а)

2б)

2а)на

2б) Пусть

, но

Используя предельный переход, можем включить точку в отрезок

Нормальные системы дифференциальных уравнений.

§1.Нормальные системы дифференциальных уравнений первого порядка.

(1.1)

заданы и непрерывны в некоторой области

- искомые функции.

Введем вектор-функцию

Лекция №8.

(1.1)

Чтобы задать задачу Коши:

, (1.2)

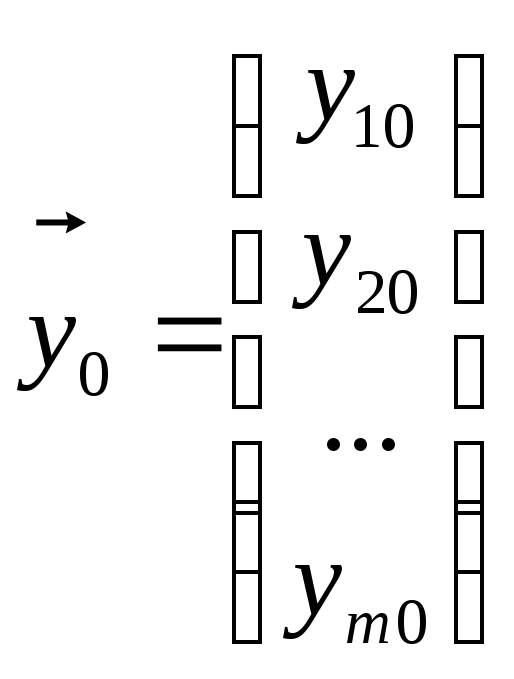
Если непрерывна в, подразумевается применимость этого свойства по всем компонентам вектор-функции.

Определение.

Вектор-функция , определенная на промежутке, называется решением системы (1.1), если

1)

2)

3)

Лемма 1.1

Вектор-функция - является решением задачи Коши (1.1), (1.2) натогда и только тогда, когда она является решением интегрального уравнения(1.3)

Пусть последовательность непрерывна навектор-функций.

Определение.

Последовательность равномерно ограничена, если

Определение.

Последовательность называется равностепенно непрерывной, если

равномерно ограничена и равностепенно непрерывна равномерно ограничена и равностепенно непрерывна для всех.

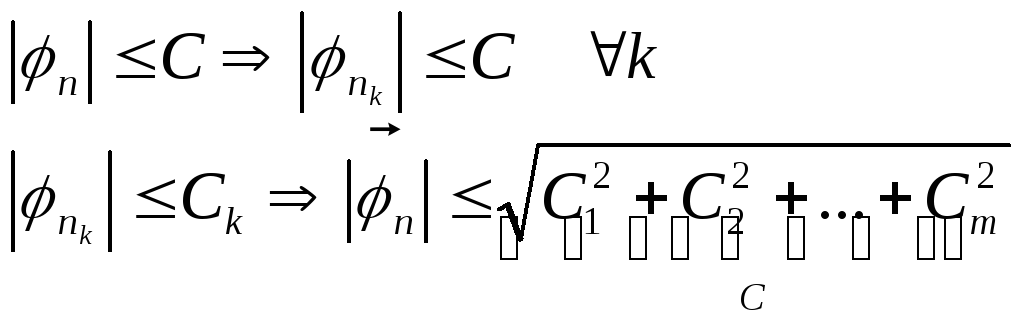
Теорема 1.1 (Лемма Асколи-Арцелла)

Если последовательность равномерно ограничена и равностепенно непрерывна на, то из нее можно выделить подпоследовательность

Доказательство.

равномерно ограничена и равностепенно непрерывна. В силу леммы Асколи-Арцелла для последовательности скалярных функций:

равномерно ограничена и равностепенно непрерывна

На - том этапе выбираем подпоследовательность- ных компонент,

Теорема 1.2 (Теорема Пеано)

Пусть . Тогда задача Коши (1.1), (1.2) имеет решение, определенное на отрезке

Доказательство.

- замкнутый шар ,- радиус.(1.4)

Вопрос: не выйдем ли за границу области ?

- равномерно ограниченна и равностепенно непрерывна. По лемме Асколи-Арцелла

-фиксир.

Устремим . Тогда

является решением (1.3), а значит и решением (1.1), (1.2).

Единственность решения задачи Коши.

Определение.

удовлетворяет в локальному условию Липшица по переменной, еслиокрестностьи постояннаятакие, что

Теорема 1.3.

Пусть . Еслиудовлетворяет влокальному условию Липшица по переменному, то решение задачи Коши (1.1), (1.2) единственно.

Доказательство.

Пусть существуют два различных решения на промежутке и.

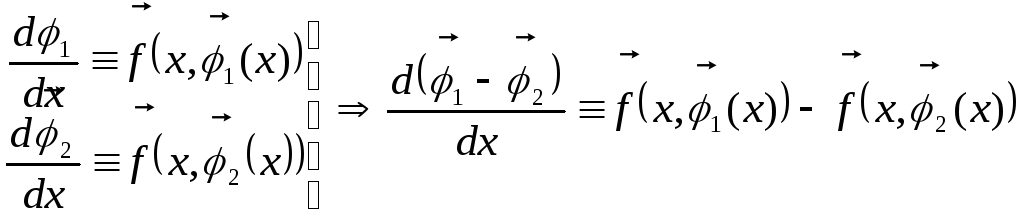
на

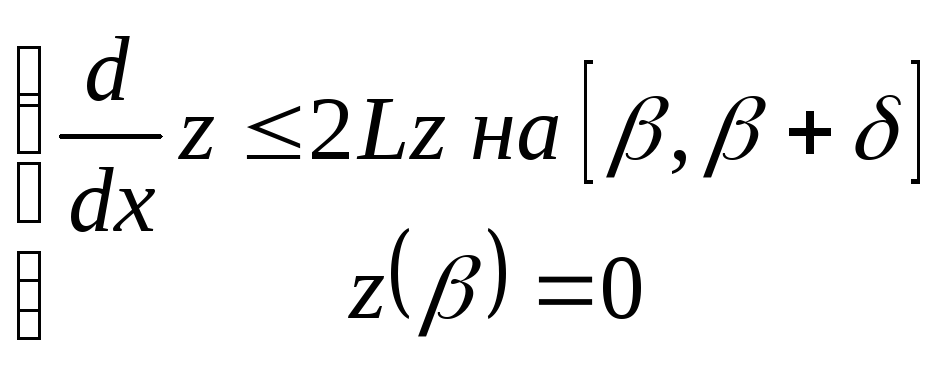
Неравенство Гронуолла:

на

Получено противоречие.

Лекция №9.

(1.1)

(1.2)

Когда правая часть удовлетворяет локальному по условию Липшица, то для случая одного уравнения:

Лемма 1.1

Пусть . Тогда

Доказательство.

Пусть

Лемма 1.2

Пусть . Тогда для всехсправедлива формула конечных приращений для вектор-функций:

Доказательство:

Утверждение 1.1

Если у существует матрица Якоби, тоудовлетворяет локальному вусловию Липшица (непрерывность в матрице подразумевает непрерывность всех ее компонент).

Доказательство.

- замкнутая окрестность. В этой окрестности любая непрерывная функция ограничена.

Продолжение решений

Все определения и утверждения, относящиеся к продолжению решений, имеют место и для системы (1.1). Следует лишь заметить