§2.Сведение систем дифференциальных уравнений произвольного порядка к системам дифференциальных уравнений первого порядка.

(2.1)

непрерывны в

- искомые функции.

Определение.

Решение системы

1. 

2. 

3. Функции обращают уравнения (2.1) в тождества.

При получаем нормальную систему дифференциальных уравнений первого порядка

Введем новые функции

(2.2)нормальная система ДУ I порядка

решение (2.1)

решение (2.2)

(2.1) (2.2)

(2.3)

(2.2)+(2.3)=задача Коши. Для (2.1) задача Коши ставится так:

(2.4)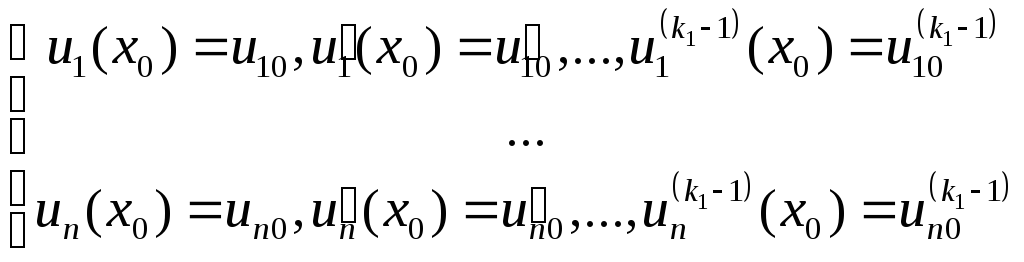

(2.2)+(2.3)(2.1)+(2.4)

Теорема 2.1. (Теорема Пеано)

Пусть и

Тогда у задачи Коши (2.1) (2.4) существует решение, определенное на некотором отрезке

Доказательство проводится сведением к системе уравнений первого порядка и применении теоремы Пеано.

Теорема 2.2

Пусть выполняются условия теоремы 2.1 и удовлетворяет локальному вусловию Липшица по переменной. Тогда решение задачи Коши (2.1), (2.4) единственно.

Лекция №10.

§3.Уравнения, допускающие понижение порядка.

(3.1)

1) не зависит от

2) не зависит от

-искомая функция.

3) однородна относительно

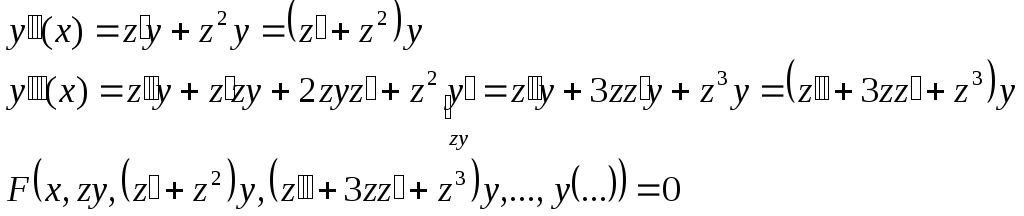
Получили дифференциальное уравнение порядка относительно переменной..

4) удовлетворяет обобщенному условию однородности.

Далее решаем по 2).

5) Уравнение имеет вид:

Общая теория линейных систем дифференциальных уравнений

, ,

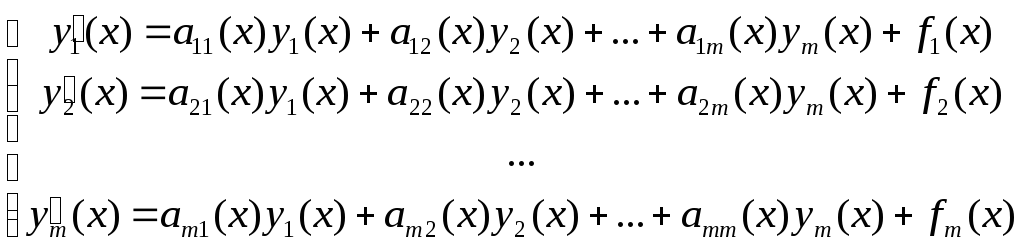
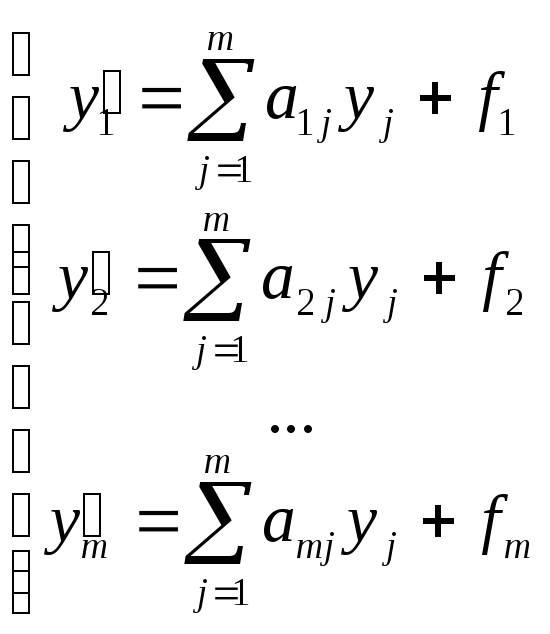
(1.1)

§1.Следствие из общей теории нормальных систем.

непрерывна на .непрерывна на.

(1.2)

Задача Коши (1.1), (1.2).

- непрерывна, значит работает теорема Пеано о существовании решения.

непрерывна, следовательно, выполняется условие Липшица.

Теорема 1.1

Решение задачи Коши (1.1), (1.2) существует, единственно и определено на .

Нельзя продолжить решение вправо.

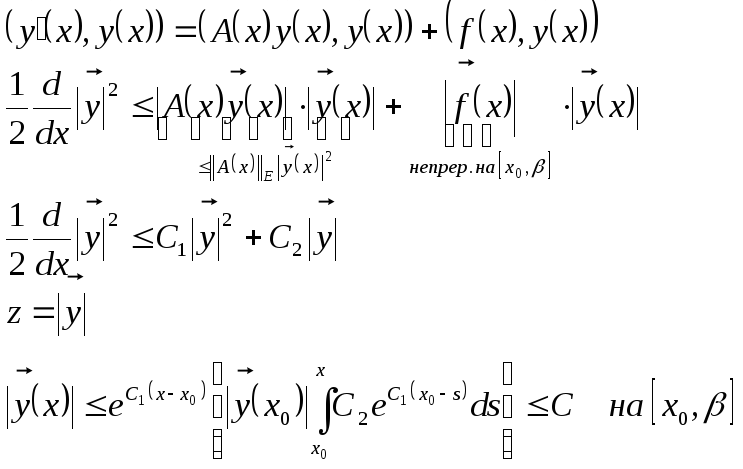
§2.Однородные системы. Определитель Вронского.

Лемма 2.1.

Если - решения системы (2.1), то- решения системы (2.1).

Доказательство.

.

Определение.

- система вектор-функций, заданных на . Эта система называется линейно зависимой, если существует нетривиальная линейная комбинация

(*) на, и называется линейно независимой, если (*) выполняется только для.

Определение.

Определителем Вронского системы вектор-функций называется.

Утверждение.

Если система линейно зависима, то.

Доказательство.

.

Теорема 2.1

Пусть - система решений однородной системы (2.1). Если,, то система- линейно зависима ина.

Доказательство.

- линейно зависима. Следовательно, существует нетривиальный набор

По лемме 2.1

. Это означает, что вектор-функции линейно зависимы.

- система решений (2.1)

Пример.

- линейно независимая система, но . Это получилось, т.к. не существует системы дифференциальных уравнений, для которойибыли бы решениями.

Лекция №11.

§3.Формула Остроградского-Лиувилля.

Лемма 3.1

Справедлива формула дифференцирования определителя:

Доказательство.

Таким образом получили формулу (3.1).

Теорема 3.1

Пусть - есть вектор-функции, являющиеся решением однородной системы. Тогда справедлива формула Остроградского-Лиувилля:

(3.2)

Доказательство.

Посчитаем определитель Вронского.

Получено уравнение с разделяющимися переменными. Интегрируем и приходим к формуле: