§3. Уравнения с разделяющимися переменными.

Уравнения с разделенными переменными.

По теореме (2.1) – общий интеграл уравнения (3.1), который может быть записан в виде:

Уравнения с разделяющимися переменными.

Можем свести это уравнение к виду:

.

Уравнения, сводящиеся к уравнениям с разделяющимися переменными.

1)

Введем функцию

2) Однородные уравнения.

, , гдеиоднородные функции одной степени однородности равной.

–однородная функция степени .

Пример.

,

Вводится замена

Возможны дополнительные решения!

Если , то

Если , то

3)

Обозначим и.

Лекция 4. Задача Коши

Теорема 5.2 (Теорем Пеано)

Пусть и. Тогда у задачи Коши (5.1) и (5.2) существует решение, определенное на некотором отрезке.

Доказательство.

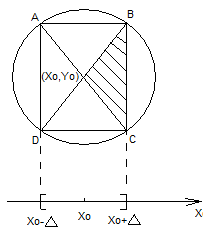
Подставляя в (5.1) получаем некоторый коэффициент

Получим некоторую ломаную (ломаную Эйлера)– некоторое приближение к искомому решению.

Заметим, что ломаная Эйлера не выйдет из области , в силу построения диагоналейAC и BD: .

,

–равномерно ограничена на (одной константой)

Неравенство гарантирует равномерную непрерывность

В силу леммы Асколи-Арцелла на

Докажем, что и есть решение задачи Коши. Фиксируем. Устремляем

Стремится ли к нулю величина

равномерно непрерывна на S:

равномерно

Переходя к пределам получаем равенство:

Аналогичные рассуждения проводим для отрезка []. Получим, что- решение задачи Коши (5.1), (5.2)

§6. Единственность решения задачи Коши.

(6.1)

(6.2)

Задача Коши (6.1), (6,2) имеет единственное решение, если любые два ее решения, определенные на одном промежутке тоже совпадают. Непрерывность не гарантирует единственность.

Пример:

В качестве решения могут выступать следующие функции:

,,, и т. д.

Лекция № 5. Единственность решения задачи Коши.

Определение.

Пусть ,. Еслиудовлетворяет локальному вусловию Липшица по переменной, если

и для

Теорема 6.1.

Пусть ,. Еслиудовлетворяет локальному вусловию Липшица по переменной, то решение задачи Коши (6.1), (6.2) единственно.

Доказательство.

Предположим, что существуют два различных решения задачи Коши, определенные на

Графики ипринадлежат

(*)

При

Противоречие.

Утверждение.

Если , тоудовлетворяет условию Липшица по переменной

Доказательство.

. - открытоесо своей окрестностью.

Определение.

удовлетворяет локальному в условию Осгуда по переменной, еслии, где- диаметр окрестности,, и при этом выполняется неравенство:

Теорема 6.2 (теорема Осгуда)

Пусть ,. Еслиудовлетворяет локальному вусловию Осгуда по переменной, то решение задачи Коши единственно.

Доказательство.

Доказательство проводится аналогично доказательству теоремы 6.1 до (*).

§7.Продолжение решений.

(7.1)

- решение уравнения (7.1), определенное на некотором промежутке

Определение.

называется продолжением решения вправо, еслиопределена на промежуткеявляется решением дифференциального уравнения (7.1) и

Аналогично вводится определение продолжения решений влево.

Определение.

Решение дифференциального уравнения, которое не может быть продолжено ни влево, ни вправо, называется полным.

Утверждение 7.1.

Пусть - решение дифференциального уравнения (7.1), определенная на промежутке. Тогда решение может быть продолжено вправо.

Доказательство.

, определенное на

В точке должна существовать производная.

Замечание.

Аналогичные рассуждения можно провести для случая продолжения решения влево.

Из доказанного следует, что на отрезке можно продлить в обе стороны.

Пример 1.

Полное на .

Пример 2.

Полное на

Лекция № 6.

Теорема 7.1

Пусть - решение дифференциального уравнения, определенное на промежутке, где. Для того, чтобы решениенельзя было продолжить вправо необходимо и достаточно, чтобы было верно, по крайней мере, одно из следующих свойств решения:

1)

2)

Примеры, приведенные выше, иллюстрируют эти свойства.