§4.Фундаментальная система решений. Структура общего решения однородной системы линейных дифференциальных уравнений.

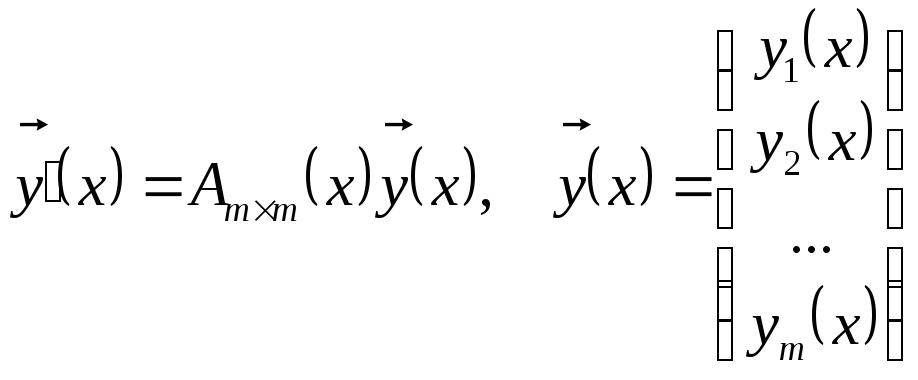(4.1)

(4.2)

(4.3)

Определение.

Система из линейно независимых вектор-функций (4.2), которые являются решениями системы (4.1), называется фундаментальной системой решений системы (4.1). Тогда матрица (4.3) , составленная из системы ФСР, называется фундаментальной матрицей.

Теорема 4.1

ФСР существуют.

Доказательство.

Рассмотрим систему (4.1) на некотором интервале и зафиксируем. Рассмотрим базис в, состоящий из функций.

- решение, соответствующее -той задаче Коши.

Определитель Вронского этих решений в т. :

(в силу линейной независимости векторов)

Воспользуемся свойством формулы Остроградского-Лиувилля, именно: раз , то.

Для того, чтобы решения были линейно независимыми, необходимо и достаточно, чтобы .

- линейно независимы, значит образуют фундаментальную систему решений.

Чтд

Теорема 4.2. Об общем решении однородной системы.

Пусть (4.2) – ФСР системы (4.1).

Тогда любое решение системы (4.1) можно представить в виде линейной комбинации

, (4.4)

где - произвольные константы.

С другой стороны, любая функция вида (4.4) является решением.

Доказательство.

Фиксируем . Пусть- произвольное решение системы (4.1).

Вычислим значения

Они ФСР, значит вектора линейно независимы, следовательно, образуют базис в пространстве .можно разложить по этому базису:

Рассмотрим функцию

с найденными .

, .

Воспользовавшись теоремой единственности, получаем .

справедливо всюду на .

Обратно.

По лемме 2.1 функция (4.4)

Чтд

Рассмотрим систему (4.2)

(4.5)

Теорема 4.3

Если непрерывно-дифференцируемые вектор-функции (4.2) удовлетворяют условию (4.5), то существует система (4.1) с ФСР (4.2).

Доказательство.

То, что (4.2) образует ФСР . Можем посчитать правую часть. Значитсуществует и единственна.

Чтд

Замечание 4.1

Вектор-функции (4.2) приудовлетворяют системе

Если разложить этот определитель по I столбцу, то получим систему (4.1)

§5.Общее решение линейных неоднородных систем. Метод вариации постоянных.

(5.1)

Лемма 5.1

Пусть - частное решение неоднородной системы (5.1), а- решение однородной системы (4.1). Тогдаявляется решением неоднородной системы (5.1).

Доказательство.

Чтд

Лемма 5.2

Пусть и- является решением неоднородной системы (5.1). Тогда их разностьявляется решением однородной системы (4.1).

Доказательство.

Чтд

Теорема 5.1. (Об общем решении неоднородной системы)

Пусть - ФСР системы (4.1), а- частное решение неоднородной системы (5.1).

Тогда решениесистемы (5.1) представимо в виде линейной комбинации

(5.2)

С другой стороны, вектор-функция (5.2) удовлетворяет системе (5.1).

Доказательство.

В силу леммы 5.2 разность - является решением системы (4.1).

В силу теоремы 4.2 можем представить любое решение однородной системы в виде линейной комбинации

(5.2)

Обратно.

Из леммы 5.1 и теоремы 4.2 получаем, что функция вида (5.2) удовлетворяет системе (5.1)

Чтд

Из этой теоремы получаем, что общее решение линейной неоднородной системы есть сумма частного решения неоднородной системы и общего решения, соответствующего однородной системе.

Лекция №12.

Метод вариации постоянных.

- ФСР

- частное решение.

-формула общего решения.

Вопрос: где взять ?