2.3.2.5. Пример применения метода Фаддеевой (Пример 2.3)

Пример П2.3: дана система

Найти Ф(p).

Решение:

Способ №1 (непосредственное вычисление).

, т.к. , тогда

, ,

;

Способ №2 (метод Сурье).

n=2, k=1, α₂ ,

α₁,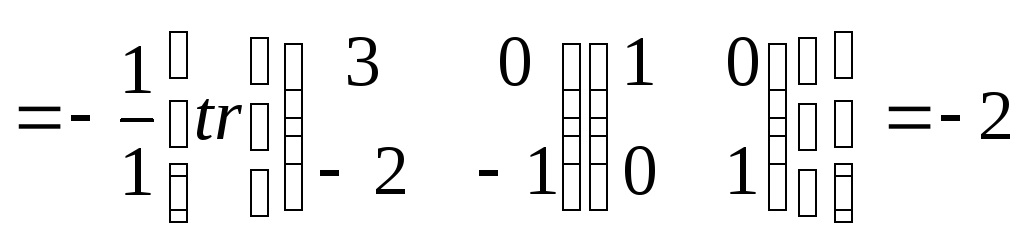

.

α₀,

.

.

2.4. Частотные характеристики (функции) систем (Лекция 6)

2.4.1. Частотная переходная функция

2.4.1.1. Напоминание о представлении комплексных чисел

Частотные характеристики характеризуют зависимость реакции системы от частоты периодического входного воздействия. Зависимость от частоты может характеризоваться изменением амплитуды и фазы входного сигнала. Для представления этих двух важнейших характеристик удобно использовать комплексные числа, которые, как известно, содержат в себе обе эти характеристики.

Поэтому вспомним формы представления комплексных чисел и используемые при этом термины. Из курса математики известно, что любое комплексное число имеет вид:

z = a + jb,

где a=Re z – его действительная часть (от латинского Realis -действительный),

b=Im z – его мнимая часть (от латинского Imaginarias - мнимый).

На комплексной плоскости комплексное число представляется в виде, показанном на рис. 2.2, где a и b – действительная и мнимая части числа, A – его модуль, а φ – аргумент.

Рис. 2.2. Представление числа на комплексной плоскости

Комплексное число можно представить также в показательной и тригонометрической форме:

z = A(z)e^{jarg z} = A(z) (cos j + j sin j),

где A(z) = - модуль комплексного числа, который в теории управления называется

амплитудой;

arg z = arctg b/a = φ – аргумент, который в теории управления называется фазой.

Выражения тригонометрических функций через показательные можно получить с помощью формул Эйлера:

cos φ = (e^jφ + e^{- jφ}) /2, sin φ = (e^jφ - e^{- jφ}) /2j.

2.4.1.2. Частотная передаточная функция

Периодическое входное воздействие можно представить в показательной форме:

w(t) = w_m e^jwt , t ³0. (2.25)

Пусть оно действует на систему

= Ax(t) + Bw(t), (2.26)

y(t) = Cx(t). (2.27)

Так как уравнение (2.26) неоднородное, то его решение состоит из суммы общего решения однородного уравнения и частного решения неоднородного. Общее решение было ранее определено. Частное решение неоднородного уравнения может быть определено в виде:

x_ч(t) = x_m e^jwt, x_m = const. (2.28)

Подставив (2.25) и (2.28) в (2.26), получим:

x_m jw e^jwt = A x_m e^jwt ₊ B w_m e^jwt,

(jwI -A)x_m e^jwt = B w_m e^jwt ,

x_ч (t) =(jwI -A)^-1 B w_m e^jwt . (2.29)

Общее решение однородного уравнения в показательной форме имеет следующий вид:

x_o (t) = e^Atx(0). (2.30)

Сумма (2.29) и (2.30) представляет собой соответствующее воздействию (2.25) решение уравнения (2.26):

x(t) = e^Atx(0) + (jwI -A)^-1B w_m e^jwt . (2.31)

Первое слагаемое этого решения характеризует переходную погрешность, а второе установившуюся.

При x(0) = 0 получим:

x(t) = (jwI -A)^-1B w_m e^jwt_.

Подставим это в (2.27) и получим для вектора выходных величин:

y(t) = Cx(t) = C(jwI -A)^-1 B w_m e^jwt . (2.32)

Функция, позволяющая определить значения компонент вектора выходных величин по значениям компонент вектора входных величин при разных значениях частоты, называется частотной переходной характеристикой системы. Из (2.32) следует её вид:

H(jw) = C(jwI -A)^-1 B (2.33)

Её можно получить заменой в передаточной функции аргумента p на jw. В рассматриваемом случае она представляет собой матрицу, количество строк в которой совпадает с размерностью вектора y, а количество столбцов - с размерностью вектора w.

Если H(jw) известно и известно входное воздействие, то можно найти выходные величины, используя известные правила перемножения комплексных чисел.