2.2. Временные характеристики систем управления (Лекция 4)

2.2.1. Линейные нестационарные системы

2.2.1.1. Общий вид описания системы

В качестве примера будут использоваться наиболее простые линейные системы.

Их движение описывается дифференциальными уравнениями вида (1.9)

= A(t)x(t) + B(t)w(t), t³t₀ , (2.4)

где x(t)-n-мерный вектор состояния,

w(t) – L-мерный вектор входных воздействий,

A(t), B(t) – функциональные матрицы, соответствующих размеров; их

элементы – функции времени.

В общем случае кроме состояний x(t), имеются выходные величины, которые могут являться алгебраической функцией состояний. Обозначим их векторy(t)и запишем в общем виде:

y(t) = C(t)x(t) , t³t_0. (2.5)

Для того, чтобы выяснить поведение объекта, надо решить (2.4), то есть найти x(t). Это неоднородное дифференциальное уравнение. Его решение состоит из общего решения однородного и частного решения неоднородного уравнения.

2.2.1.2. Решение однородного уравнения

Однородное уравнение из (2.4) имеет вид:

. (2.6)

Общее решение однородного уравнения (2.6) может быть определено в виде:

x₀(t) = Ф(t,t₀) x(t₀), (2.7)

где х_О(t) – обозначено общее решение,

- начальные условия, которые должны быть заданы,

Ф(t,t₀) – фундаментальная матрица, которая в соответствии с (2.6), (2.7) должна удовлетворять уравнениям:

(2.8)

Из (2.8) видно, что фундаментальная матрица является функциональной, т.е. её элементами являются функции φ_ij(t,t­₀), i,j = 1, 2, … , n, где n – порядок системы (матрицы А(t)). Практически, используя (2.8) непосредственно, найти решение, т.е. функции φ_ij(t,t­₀), i,j = 1, 2, … , n, не представляется возможным и для определения фундаментальной матрицы используются специальные методы. Однако в простейших случаях это возможно и будет показано ниже.

2.2.1.3. Решение неоднородного уравнения

Частное решение неоднородного уравнения (2.4) может быть определено в виде:

x_ч (t) = Ф(t,t₀) v(t), (2.9)

где v(t) - неизвестная функция, которую следует определить так, чтобы удовлетворялось (2.4). Подставив (2.9) в (2.4), получаем:

dx_ч (t)/dt = v(t) + Ф(t,t₀), далее, раскрывая левую часть имеем:

A(t) Ф(t,t₀)v(t) + Ф(t,t₀) = A(t) Ф(t,t₀)v(t) + B(t) w(t),

откуда

= Ф^-1(t,t₀) B(t) w(t),

v(t) = . (2.10)

Заметим, что т.к. в (2.10) t становится верхним пределом интеграла, то переменная интегрирования под знаком интеграла обозначена другой буквой.

Подставив (2.10) в (2.9), получаем окончательное выражение частного решения (2.4) в виде:

. (2.11)

Общее решение векторно-матричного уравнения (2.4) представляет сумму общего решения однородного уравнения и частного решения неоднородного x(t) = x₀(t) + x_ч(t). В результате имеем:

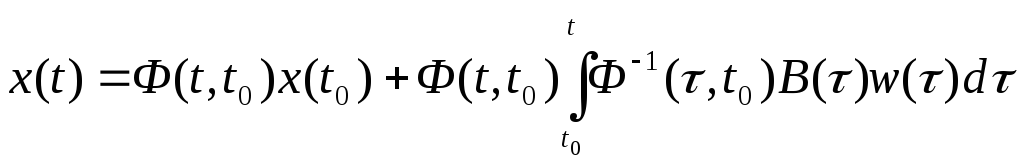. (2.12а)