Локальная теорема Лапласа

Пусть в каждом из n одинаковых независимых испытаний вероятность появления некоторого события А равна p (p0 и p1), тогда вероятность того, что событие А наступит ровно k раз в n испытаниях Р_n(k) может быть приближенно (тем точнее, чем больше n) вычислена по формуле.

Р_n(k) =  (х), (13)

где функция

, (14)

а .

В каждом учебнике по теории вероятностей имеется таблица значений функции (х), однако значение функции (х) можно вычислять и непосредственно по формуле (14). При этом следует помнить свойства функции (х). Эта функция четная, т.е. (-х) = (х), и значения функции для х4 столь малы, что их принято считать равным нулю. Следует учитывать также, что применение локальной теоремы Лапласа вместо формулы Бернулли, целесообразно (не приводят к существенным погрешностям) в случае, если npq 10.

Покажем, как работает локальная теорема Лапласа при решении предыдущей задачи.

Поскольку n = 400, p = 0,2, q = 1-p = 0,8, k = 80, то согласно теореме (поскольку npq = 4000,20,8 = 64  10)

P₄₀₀(80) = .(х) = (х).

При этом х = = = 0.

По таблице находим (0) = 0,3989, и стало быть искомая вероятность

Р₄₀₀(80) = 0,3989 = 0,04986.

Пример

Найти вероятность того, что в результате 405 бросаний игральной кости ровно 30 раз выпадает 6 очков.

Поскольку вероятность выпадения 6 очков в одном бросании кости р = , а вероятность не выпадения 6 очков q = 1-p =1 - = , npq = 405  = 10, то, используя локальную теорему Лапласа, получим:

Р₄₀₅(30)  (х),

При этом

= = = = .

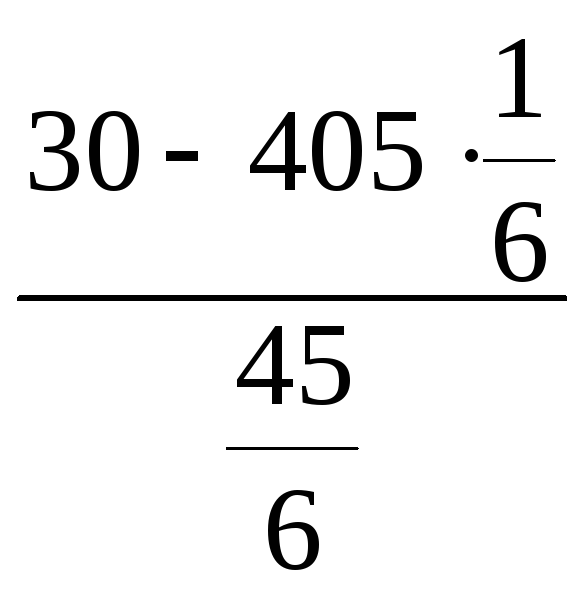
Согласно свойствам функции (х), (-5) = (5) и поскольку значение аргумента х = =54, то можно считать (5)  0, а, следовательно, искомая вероятность

Р₄₀₅(30)   (5) = 0 = 0.

Интегральная теорема Лапласа

Во многих случаях возникает необходимость в условиях ранее сформулированного эксперимента из n независимых одинаковых испытаний определить вероятность того, что интересующее нас событие появится не менее k₁ и не более k₂ раз (такая вероятность обычно обозначается Р_n(k₁, k₂)). Ответ на этот вопрос позволяет получить интегральная теорема Лапласа.

Интегральная теорема Лапласа. Пусть проводятся n независимых одинаковых испытания, в каждом из которых вероятность появления события А равна р (р 0 и р 1). Тогда вероятность Р_n(k_1, k₂) того, что событие А появится в n испытаниях не менее k₁ и не более k₂ раз приближенно равна

Р_n(k_1, k₂) = Ф(х")-Ф(х'), (15)

где Ф(х) = 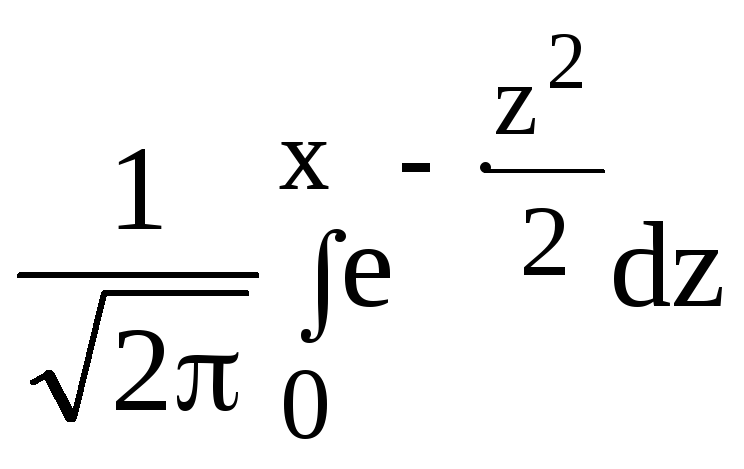- функция Лапласа. Вычисление функции Лапласа может быть произведено почленным интегрированием ряда . Для упрощения вычислений применяются таблицы функции Лапласа, которые имеются в каждом учебнике по теории вероятностей. В таблицах функции Лапласа x меняется от 0 до 5. Если x отрицательно, то нужно воспользоваться нечетностью функции, т. е. Ф(-x) = -Ф(x), а при значениях х > 5 функция Лапласа с большой степенью точности равна 0,5.

Значения х' и х" в формуле (15) определяется отношениями

х' = , х" = . (16)

Пример 1. Партия деталей содержит 20% брака. Найти вероятность того, что среди 400 проверенных изделий попадется не менее 50 и не более 90 бракованных.

Поскольку n достаточно велико, а npq = 4000,20,8  10, используют интегральную теорему Лапласа n = 100, p = 0,2, q = 0,8, k₁ = 50, k₂ = 90 по формулам (16)

k' = = = -3,75,

k" = = = 1,25,

следовательно, искомая вероятность найдется по формуле (15)

Р₄₀₀(50; 90)  Ф(1,25)- Ф(-3,75) = Ф(1,25)+ Ф(3,75)

и по таблице функции Лапласа

Р₄₀₀(50; 90)  0,3944+ 0,4970 = 0,8924.