Теоретические сведения и методические рекомендации
по решению задач
Метод непосредственного интегрирования
Нахождение интегралов с использованием основных свойств неопределённых интегралов и таблицы простейших (табличных) интегралов называется непосредственным интегрированием.
Свойства неопределённого интеграла
1. d f (x)dx = f (x)dx .
2. d (f (x)) = f (x) +C .
Эти свойства непосредственно следуют из определения первообразной.
3. Если k – постоянная величина, то
kf (x)dx = k f (x)dx , k – постоянная.
Постоянный множитель выносится за знак интеграла.
4. ( f1(x) + f 2 (x))dx = f1(x)dx + f 2 (x)dx .
Интеграл от алгебраической суммы двух (или нескольких) функций равен сумме интегралов от этих функций (при условии их существования).
Рассмотрим несколько примеров нахождения неопределённых интегралов, используя только их свойства и таблицу основных интегралов.
Приведённые ниже интегралы (1 – 6) содержат степенную функцию xa ; к такому виду следует приводить подынтегральную функцию, используя свойства степеней:
Нахождение таких интегралов основано на использовании формулы 1 из таблицы интегралов
Нахождение интегралов (7 – 10) предполагает использование первых двух свойств неопределённого интеграла.
Метод непосредственного интегрирования может удачно сочетаться с тождественными преобразованиями подынтегральной функции, которые сводят искомый интеграл к одному или нескольким табличным интегралам. В примерах (11 – 19) используются тождественные преобразования: раскрытие скобок (11, 12, 15, 16), почленное деление слагаемых числителя дроби на общий знаменатель (13, 14, 15, 16);
группировка слагаемых (18); применение тригонометрических формул (17).
II.Метод ввода новой переменной
В некоторых
случаях нахождение интеграла упрощается
при переходе к другой переменной
интегрирования. При этом если исходная
и новая переменные
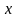и
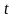связаны соотношением
,
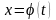где
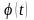- обратимая дифференцируемая функция,
то для интегралов справедливо равенство
,
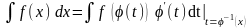в правой части которого после
вычисления интеграла следует сделать
обратную замену
.
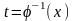В частности,
используя замену
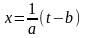(или
),
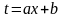получаем формулу
,
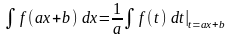позволяющую обобщить табличные интегралы. Например:
(
),
,
,
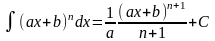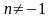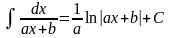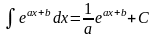где
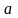и
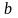- произвольные постоянные,
.
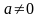Примеры. Найдем интегралы, применяя полученные формулы:
а)
;
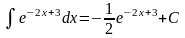б)
;
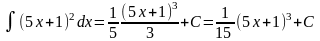в)
;
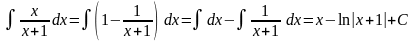г) интеграл
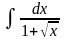найдем, сделав замену
,
.
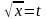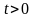Тогда
,
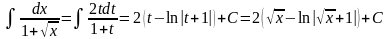где использован результат примера в);
д)
.
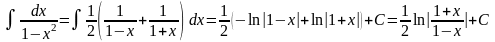Задание для практической работы
Найти неопределённый интеграл, используя таблицу интегралов
Контрольные вопросы
Какие методы интегрирования вам известны?
Запишите свойства неопределённого интеграла.
Запишите по памяти табличные интегралы
Практическое занятие №7
Тема: Интегрирование по частям
Цель: Проверить на практике умение находить неопределённый интеграл методом интегрирования по частям.
Задачи:
• развитие творческого профессионального мышления;
• познавательная мотивация;
• овладение языком науки, навыки оперирования понятиями;
• углубление теоретической и практической подготовки;
• развитие инициативы и самостоятельности студентов.
Обеспечение практического занятия:
Теоретический материал методической рекомендации к практической работе.
Ход практического занятия.
1.Формулирование темы занятия, пояснение связи темы с другими темами учебной дисциплины;
2.Проверка готовности студентов к занятию;
3.Проведение непосредственно занятия согласно тематике и в соответствии с рабочей программой дисциплины:
› Изучить теоретический материал по теме «метод интегрирования по частям»
› Рассмотреть примеры решения типовых заданий.
› Выполнить самостоятельную работу .
› Ответить на контрольные вопросы.
Краткий теоретический материал
Задание выполняемые студентами на доске
