1. Неопределённость , где с - постоянная

Если получаем неопределённость 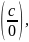то предел будет равен 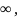так как отношение постоянной к бесконечно малой равно

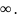
Пример 3. Найди предел функции

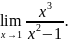
Решение:

=

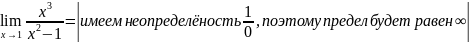
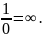
Ответ:

2. Неопределённость , где с – постоянная

Если получаем неопределённость 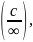то предел будет равен 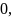так как отношение постоянной к бесконечно большой, есть величина бесконечно малая.

Пример 4. Найди предел функции

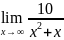
Ответ: 0.

3. Неопределённость

Для раскрытия неопределённостей вида , когда мы имеем дело с рациональными и иррациональными выражениями будем применять два способа.

1. Если в числители и знаменатели дроби стоят целые рациональные выражения, то раскладываем числитель и знаменатель дроби на множители и затем сокращаем дробь. Находим предел полученной функции.

Пример 5. Вычислить предел: .

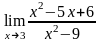Решение: При подстановке предельного значения аргумента х = 3 числитель и знаменатель дроби стремятся к нулю. Имеет место неопределенность . Разложим выражение в числителе и знаменателе и произведем сокращение на (х - 3).

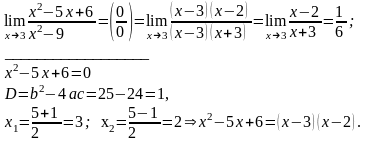х² – 9 =(х – 3)(х + 3)

Ответ:

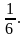
2. Если в числители (знаменатели) дроби стоит иррациональное выражение, то умножаем числитель и знаменатель дроби на сопряженный множитель иррациональному выражению, затем сокращаем дробь. Находим предел полученной функции.

Пример 6. Вычислить предел: .

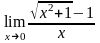Решение:

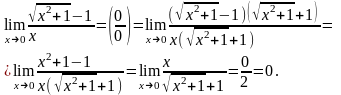
Ответ: 0.

4.Неопределённость

При отыскании предела отношения двух целых многочленов относительно х при 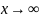оба многочлена, стоящие в числители и знаменатели дроби, нужно разделить на хⁿ, где n – наивысшая степень этих многочленов.

Аналогичный приём деления числителя и знаменателя дроби на на хⁿ, где n – наивысшая степень этих многочленов можно применять и для дробей содержащих иррациональности то есть выражения стоящие под знаком корня.

Пример 8. Вычислить предел: .

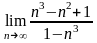Решение:

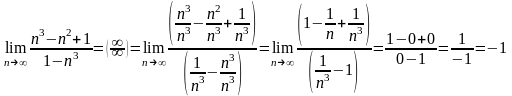
Ответ: -1.

Пример 9. Найдите предел

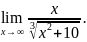
5.Неопределённость (

Контрольные вопросы

1. Какое равенство мы применяем при нахождении пределов функции?

2. Какие виды неопределённостей вам известны?

3. Что значит раскрыть неопределённость?

4. Чему равна неопределённость , где с – постоянная?

5. Чему равна неопределённость , где с – постоянная?

6. Как раскрыть неопределённость 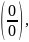когда в числители и знаменатели стоят целые рациональные выражения?

7. Как раскрыть неопределённость когда в числители и знаменатели стоят иррациональные выражения?

8. Как раскрыть неопределённость при ?

9. Как раскрыть неопределённость(

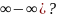
Задания для практической работы

Найти указанные пределы

№1

№2

№3

№4

№5

№6

Решение типового варианта

Практическое занятие №2

Тема: Вычисление пределов функций с использованием первого и второго замечательного пределов

Цель: Приобретение базовых знаний в области фундаментальных разделов математики. Повторить и систематизировать знания по данной теме.

Проверка усвоения знаний по вычислению пределов функций с использованием первого и второго замечательного пределов

Задачи:

• развитие творческого профессионального мышления;

• познавательная мотивация;

• овладение языком науки, навыки оперирования понятиями;

• овладение умениями и навыками постановки и решения задач;

• углубление теоретической и практической подготовки;

• развитие инициативы и самостоятельности студентов.

Обеспечение практической работы:

Теоретический материал методической рекомендации к практической работе.

Учебники: Богомолов Н.В. «Математика». – М.: Дрофа, 2009.

Индивидуальные карточки с вариантом практической работы.

Ход практического занятия.

1.Формулирование темы занятия, пояснение связи темы с другими темами учебной дисциплины;

2.Проверка готовности обучающихся к занятию;

3.Проведение непосредственно занятия согласно тематике и в соответствии с рабочей программой дисциплины:

› Повторить теоретический материал по теме «Вычисление пределов функции с использованием первого и второго замечательного пределов». › Рассмотреть примеры решения типовых заданий. › Ответить на контрольные вопросы. › Выполнить практическую работу №1.

Теоретический материал и примеры решения типовых заданий

Для приобретения практических навыков нахождения пределов рассмотрим несколько примеров. При этом при раскрытии неопределенностей будем использовать замечательные пределы: