Индуктивный элемент l

Идеализированный индуктивный элемент (рис. 3.8 – а) линейный; б) нелинейный; в) параметрический) учитывает наличие магнитного поля в устройстве и позволяет реализовать дифференциальную связь между напряжением и током при создании математической модели. В качестве индуктивности чаще всего используют катушки, содержащие много витков. При протекании тока внутри катушки создается магнитный поток Ф, который при отсутствии ферромагнитного сердечника прямо пропорционален току и числу витков w (Ф=kiw). Для подобных катушек вводится понятие потокосцепления , которое равно  = wФ. Характеризуется индуктивный элемент зависимостью потокосцепления от тока, так называемой вебер-амперной характеристикой (ВбАХ) (рис. 3.9; 1 – линейная, 2 – нелинейная индуктивности):  = f(i_L).

Напряжение на элементе по закону электромагнитной индукции прямо пропорционально скорости изменения потокосцепления:

u_L(t) = – е(t) = ; (t) = = (0) + .

Оказывает сопротивление только переменному току. Сопротивление обусловлено возникающей ЭДС самоиндукции, которая действует встречно току при его увеличении и в обратном направлении – при его уменьшении.

Для линейного индуктивного элемента –  = L·i_L, L – коэффициент пропорциональности, называемый индуктивностью; измеряется в Генри (Гн=Вб/А). Он характеризует свойства самой катушки и зависит от ее формы и геометрических размеров, квадрата числа ее витков и от магнитных свойств среды, в которой она находится.

u_L(t) = L ; i_L(t) = i_L(0) + .

Из-за сопротивления изменениям скорости переноса заряда индуктивность аналогична массе или инерции. Индуктивность не позволяет току изменяться мгновенно.

Индуктивность способна запасать энергию в магнитном поле. Мощность, потребляемая индуктивностью из цепи p_L = u_L·i_L = L·i_L , а запасаемая энергия

w(t) = = = = 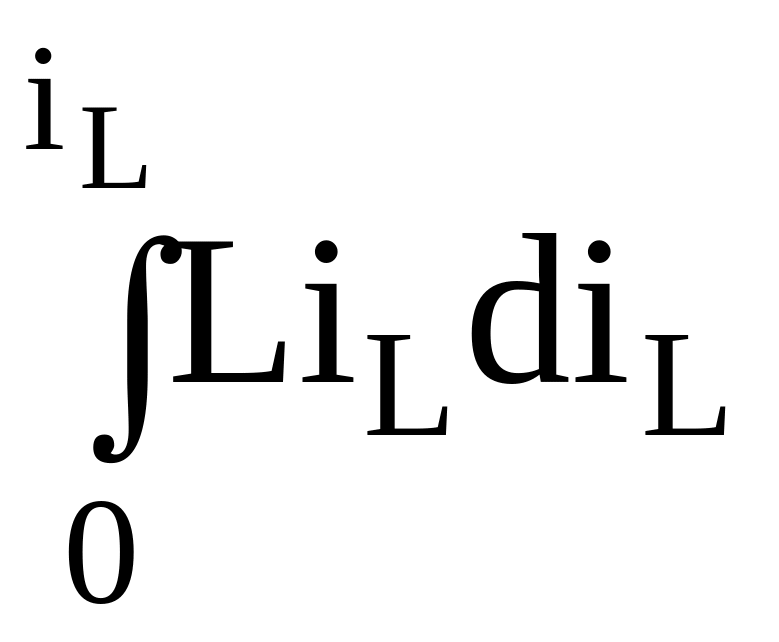½L[i_L(t)]².

П усть ток i_L(t) = I_Lm·sin(t+_i) (рис. 3.10). напряжение u_L(t) будем находить по закону электромагнитной индукции:

u_L(t) = L = L [I_Lm·sin(t + _i)] =

= L··I_Lm·cos(t + _i) = x_L·I_Lmsin(t + _i + 90) = U_Lm·sin(t + _u).

Здесь величина x_L=L [ Гн= Ом·с=Ом] обладает размерностью сопротивления и поэтому называется индуктивным (реактивным) сопротивлением синусоидальному переменному току.

Отметим, однако, что закон Ома, несправедливый для мгновенных значений, выполняется для действующих значений и амплитуд:

u_L(t)  x_L·i_L(t), U_L = x_L·I_L, U_Lm = x_L·I_Lm.

Наконец, видим, что по фазе напряжение на индуктивности опережает ток на +90^о: _u= _i + 90^o.

p_L(t) = u_L(t)·i_L(t) = U_L I_L sin(t + _u)·sin(t + _i) =

= 2·U_L·I_L·½·[cos( – ) – cos( + )] = U_L·I_L[– cos(2t + 2_i + 90^o)] =

= U_L·I_L·sin[2(t + _i)].

Мгновенная мощность индуктивного элемента является чистой синусоидой, но удвоенной частоты. Следовательно, активная мощность индуктивностью не потребляется: P_L = 0. Такие элементы называются реактивными.

Запасенная в магнитном поле индуктивности энергия

w_L(t) = + w_L(0),

где энергия в момент t = 0 равна

w_L(0) = L = L = L·I²·½ [1 – cos2_i] = [1 – cos2_i].

Таким образом,

w_L(t) = [-cos(2t + 2_i)] + [1 – cos2_i] = [1 – cos(2t + 2_i)] =

= L·I²·½ [1 – cos(2t + 2_i)] = L ,

так как = (I_m·sin(t + _i))² = I ·sin²(t + _i) = ·[1 – cos(2t + 2_i)].

Векторная диаграмма имеет вид рис. 3.11.

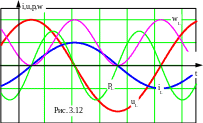
Временные графики на рис. 3.12. Энергия w_L(t) имеет пульсирующий характер и каждые полпериода проходит нулевое значение. Это означает, что в цепи имеет место обмен энергией между источником и индуктивностью. Произведение действующих значений напряжения и тока Q_L = U_L·I = х_L·I² имеет размерность В·А подобно мощности. Поэтому называется реактивной индуктивной мощностью. Измеряется в вар. Она равна

Q_L = 2·w_Lср = p_Lmax,

т о есть реактивная мощность равна амплитудному значению мгновенной мощности.