1.15 Резонанс струмів у коливальному контурі

Знайдемо закон зміни струму в коливальному контурі при сталому режимі вимушених коливань. Для цього візьмемо похідну за часом із (1.61)

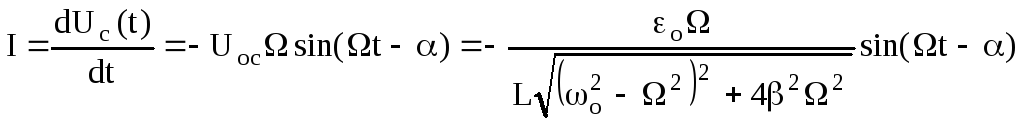.(1.68)

Амплітуда струму теж залежить від частоти Ω

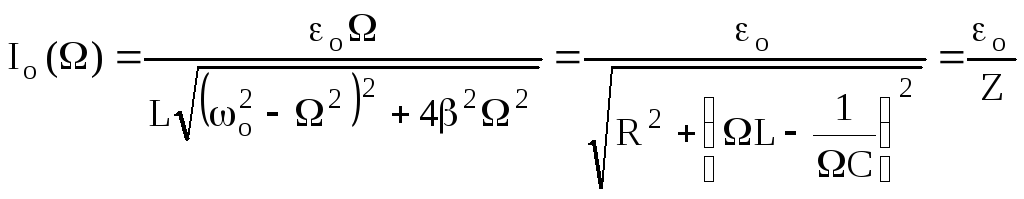. (1.69)

Знайдемо резонансну частоту для струму.

.

Одержуємо , (1.70)

щ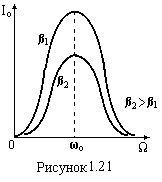о резонанс струму має місце при частоті ω_о власних незатухаючих коливань і на відміну від резонансу напруг не залежить від коефіцієнта затухання. Резонансні криві для струму зображені на рис.1.21.

, .

Із зростанням коефіцієнта затухання β амплітуда струму при резонансі зменшується.

1.16 Векторні діаграми

Запишемо закон зміни заряду q(t), напруг на опорі U_R(t), на конденсаторі U_c(t) і на котушці U_L(t) як функції часу при сталому режимі вимушених коливань під дією зовнішньої е.р.с. .

див.(1.60), ,

,

,

,

.

Векторна діаграма – це графічне зображення змінних по гармонічному закону напруг і струмів у вигляді векторів, що обертаються проти годинникової стрілки з кутовою швидкістю Ω. Довжина векторів дорівнює амплітудам у відповідному масштабі, а початкове положення задається початковою фазою, відрахованою від осі абсцис. (див.§1.8). Векторні діаграми наглядно показують фазові співвідношення між струмами і напругами в колі змінного струму.

П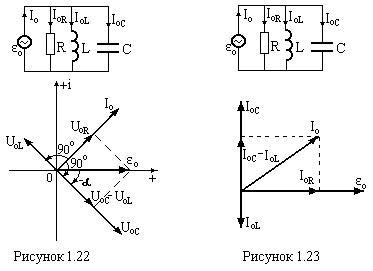 орядок побудови векторних діаграм.

Спочатку на комплексній площині будується вектор загальної для всіх елементів схеми: струм для послідовно з’єднаних елементів (див. рис.1.22), напруга для паралельного з’єднання елементів (див. рис.1.23). До цього вектора добудовуються інші, враховуючи, що напруга на опорі R співпадає по фазі із струмом, напруга U_L на котушці випереджає струм на 90⁰ (відраховується від струму проти годинникової стрілки), а на конденсаторі відстає від струму на 90⁰ (відраховується від струму по годинниковій стрілці). Якщо діаграма побудована правильно, то у відповідності із законами Кірхгофа сума напруг на послідовно з’єднаних елементах повинна дорівнювати зовнішній е.р.с., а сума струмів у паралельних вітках дає струм до розгалуження.

2 Хвилі

2.1 Механізм утворення хвиль у пружному середовищі. Класифікація хвиль. Рівняння хвиль

При коливанні тіла в пружному середовищі частинки середовища, які безпосередньо дотикаються до поверхні тіла теж приходять у вимушені коливання. За рахунок сил зв’язку в коливальний рух утягуються більш віддалені шари середовища. Виникають деформації і сили пружності, які приводять в коливання все більш віддалені шари середовища. Таким чином кожна частинка середовища здійснює вимушені коливання навколо свого положення рівноваги. В середовищі ж з певною швидкістю поширюється стан деформації, а перенесення речовини середовища немає. Такий процес поширення коливань в середовищі називається хвильовим процесом, або просто хвилею.

В залежності від напрямку коливань частинок середовища і напрямку поширення хвиль вони поділяються на повздовжні і поперечні. У повздовжніх хвилях частинки середовища коливаються в напрямку поширення хвиль, а в поперечних – перпендикулярно до нього.

При повздовжніх хвилях виникають деформації розтягування (стиснення), які мають місце як у твердих тілах, так і в рідинах та газах. Отже повздовжні пружні хвилі можуть поширюватись у трьох агрегатних станах речовини. В поперечних хвилях виникають деформації здвигу. Тому такі хвилі можуть поширюватись в твердих тілах.

Фронтом хвилі називається геометричне місце точок середовища, які в даний момент починають коливатись, тобто до яких дійшов стан деформації. В залежності від форми фронту хвилі поділяються на плоскі, сферичні, циліндричні, еліптичні і т.д.

Хвильовою поверхнею називається геометричне місце точок середовища, які коливаються в однаковій фазі. Отже фронт хвилі це одна із хвильових поверхонь.

Довжина хвилі λ – це відстань, на яку переміщується із швидкістю фронт хвилі за один період Т коливання елементів середовища

. (2.1)

Знайдемо рівняння хвилі, яке повинне давати можливість знайти зміщення S від положення рівноваги будь-якої точки середовища в довільний момент часу. Отже це функція S=S(x,y,z,t) чотирьох аргументів: координат і часу. Нехай джерело плоскої хвилі знаходиться в початку координат і починає коливатися по гармонічному закону

. (2.2)

Плоска хвиля поширюється із швидкістю υ в напрямку одиничного вектора , який перпендикулярний до хвильової поверхні (рис.2.1). Точки, віддалені від джерела на відстань ℓ, почнуть коливатися пізніше від джерела на час затримки . Положення точок хвильової поверхні задамо радіус-вектором , який утворює з напрямком ℓ кут φ. Із простих геометричних міркувань і означення скалярного добутку векторів можемо записати

. Із врахуванням (2.2) і запізнення початку коливань на час τ закон коливання точок хвильової поверхні набуде виду

. (2.3)

Враховуючи (2.1) та означення циклічної частоти (1.23), відношення . k називається хвильовим числом. Його вважають вектором, направленим перпендикулярно до хвильової поверхні, тобто співпадає з нормальним вектором , тобто

. (2.4)

Таким чином, рівняння хвилі (2.3) набуває виду

. (2.5)

Рівняння хвилі можна записати і в показовій формі

. (2.6)