3. Борівська теорія воднеподібних атомів. Закономірності лінійчатих атомних спектрів

Воднеподібний атом (йон) – це йон із зарядом ядра +Ze навколо якого обертається лише один електрон, як і в атомі водню. До таких атомів відносяться йонізований гелій He⁺, двічі йонізований літій Li²⁺, тричі йонізований берилій Be³⁺, чотири рази йонізований бор B⁴⁺ і т.д.

Розглянемо електрон, що рухається в полі атомного ядра ­­+Ze. Для спрощення розрахунків вважатимемо, що електрон масою m рухається по коловій орбіті радіусом r_n із швидкістю υ під дією сили Кулона. Запишемо основне рівняння динаміки обертального руху і постулат квантування орбіт (6.2)

Із системи цих рівнянь знайдемо радіус орбіти r_n, вилучивши швидкість υ. Із (6.5) знаходимо швидкість і підставляємо в (6.4)

;

. (6.6)

Для атома водню Z = 1. Радіус найближчої до ядра орбіти при n = 1

.

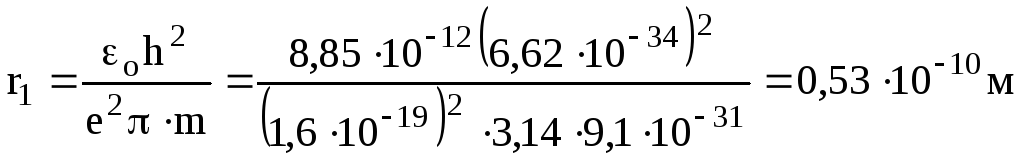Це значення відповідає розмірам атома водню, які знайдені з кінетичної теорії газів.

Знайдемо повну енергію електрона, яка складається з потенціальної енергії взаємодії з ядром і кінетичної енергії руху по орбіті

. (6.7)

Підставляємо із (6.4) , а потім радіус (6.6). Одержуємо

. (6.8)

Для атома водню Z = 1; . При n = 1 одержуємо теоретичне значення енергії іонізації атома водню 13,6 еВ, що добре узгоджується з експериментом.

Намалюємо енергетичний спектр атома водню і електронні п ереходи, при яких енергія атомом випромінюється (рис.6.7).

Експериментально певна закономірність в атомних спектрах у видимому діапазоні була вперше знайдена швейцарським вчителем у 1885 році І.Бальмером (1825-1898) як плід довготерпіння в переборі чисел. Він одержав формулу, яка носить його ім’я

, (6.9)

де ν – частота спектральної лінії, R_ν = 3,29∙10¹⁵ Гц – емпірично підібрана стала, яка називається сталою Рідберга, n = 3, 4, 5,…

У теорії Бора стала зрозумілою формула Бальмера (6.9), а також були передбачені спектральні серії в ультрафіолетовій області (див. рис.6.7 серія Лаймана) і в інфрачервоній області (див. рис.6.7 серії Пашена, Брекета.). Спектральні лінії систематизують по серіям, в залежності від того, на який енергетичний рівень переходить електрон із більш високих рівнів: на 1-й рівень – серія Лаймана, на 2-й – серія Бальмера , на 3-й – серія Пашена, на 4-й – серія Брекета і т.д.

Скориставшись формулами (6.3) та (6.8), знайдемо частоти спектральних ліній

. (6.10)

Тут – теоретичне значення сталої Рідберга, яке, як видно, добре узгоджується із емпіричним значенням.

Таким чином, теорія Бора пояснила механізм виникнення спектральних ліній та їх закономірності, одержане теоретичне значення сталої Ридберга, передбачила спектральні серії в невидимій області спектру. Але кількісного узгодження в спектрах уже для атома гелію не давала. В цьому полягає основний недолік теорії. Це обумовлене тим, що теорії Бора притаманна внутрішня суперечність. У ній класична фізика штучно поєднується з квантовими постулатами, тобто вона була ні послідовно класичною ні послідовно квантовою.