
- •Практическая работа № 30 Нахождение производных элементарных функций
- •Средства обучения:
- •Практическая работа № 31 Нахождение производной сложной функции
- •Средства обучения:
- •Практическая работа № 32 Применение производной первого порядка к исследованию функции на монотонность и экстремумы функции
- •Средства обучения:
- •Практическая работа № 33 Решение задач прикладного характера на нахождение наибольшего и наименьшего значения функции
- •Средства обучения:
- •Практическая работа № 34 Применение производной второго порядка к исследованию графика функции на выпуклость и перегиб
- •Средства обучения:
- •Практическая работа № 35 Построение графика функции с помощью производной
- •Средства обучения:
- •Практическая работа № 36 Нахождение неопределённого интеграла
- •Средства обучения:
- •Практическая работа № 37 Вычисление определённого интеграла. Решение задач физического и геометрического содержания с помощью определённого интеграла
- •Средства обучения:
- •Приложения определенного интеграла
- •1. Вычисление площади плоской фигуры.
- •2. Вычисление пути, пройденного точкой.
- •3. Вычисление работы силы.
- •Практическая работа № 38 Решение задач с использованием основных теорем стереометрии и вычислением угла между прямой и плоскостью
- •Средства обучения:
- •Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. Перпендикулярность прямой и плоскости
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 39 Решение задач на двугранный угол
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 40 Изображение пространственных фигур в стереометрии. Решение задач на вычисление площади ортогональной проекции фигуры
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 41 Построение развёртки призмы и параллелепипеда
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 42
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 43 Решение задач прикладного характера на вычисление площади поверхности тела с использованием знаний о призме
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 44 Построение развёртки пирамиды полной и усечённой
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 45 Вычисление площади боковой и полной поверхностей пирамиды полной и усечённой
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 46 Решение задач прикладного характера на вычисление площади поверхности тела с использованием знаний о пирамиде
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 47 Построение сечений куба, призмы и пирамиды
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 48 Построение развёрток правильных многогранников
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 49 Построение развёртки цилиндра
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 50 Построение развёртки конуса, усечённого конуса
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 51 Решение задач на нахождение основных элементов тел вращения
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 52 Решение задач по теме «Шар и сфера»
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 53 Вывод формул для вычисления объёмов параллелепипеда, призмы, цилиндра
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 54 Вывод формул для вычисления объёма пирамиды и конуса, объёма шара
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 55 Решение задач на вычисление объёмов геометрических тел
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 56 Вывод формул для вычисления площадей поверхностей тел вращения
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 57 Решение задач на вычисление площади поверхности тел вращения
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 58 Решение задач прикладного характера на вычисление объёмов и площадей поверхностей геометрических тел
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 59 Решение задач на составление уравнений прямой и плоскости в пространстве
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 60 Решение задач с использованием уравнения сферы
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 61 Действия над векторами в пространстве
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 62 Разложение вектора в пространстве. Нахождение координат вектора в заданном базисе
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 63 Решение задач на вычисление скалярного произведения двух векторов, использование свойств скалярного произведения, нахождение угла между векторами
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 64 Решение задач с использованием координатно-векторного метода
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 65 Решение комбинаторных задач
- •Средства обучения:
- •Практическая работа № 66 Формула бинома Ньютона
- •Средства обучения:
- •Практическая работа № 67 Решение задач на определение вероятности случайного события
- •Средства обучения:
- •9. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
Практическая работа № 36 Нахождение неопределённого интеграла
Цель: научиться находить неопределенные интегралы методами непосредственного интегрирования, заменой переменной и по частям.
Место проведения: учебная аудитория, ОБОУ СПО «КЭМТ».
Средства обучения:
методические рекомендации к практической работе № 36.
Для выполнения задания необходимо:
знать:- определение первообразной функции;
- понятие неопределённого интеграла;
- свойства неопределённого интеграл;
- формулы интегрирования.
уметь:- находить неопределённые интегралы методом непосредственного интегрирования, методом подстановки и методом интегрирования по частям.
Рекомендации по выполнению заданий:
1. Повторите пройденный материал согласно требованиям к знаниям.
2. Прочтите краткую теоретическую справку.
3. Выполните с помощью преподавателя в случае необходимости практические задания для аудиторной работы, которые включают следующие виды работ:
вычисление неопределенных интегралов методом непосредственного интегрирования;
вычисление неопределенных интегралов методом подстановки;
вычисление неопределенных интегралов методом интегрирования по частям.
4. Выполните задания для самостоятельной работы в соответствии с вашим вариантом, пользуюсь алгоритмом выполнения аудиторных заданий.
5. Оформите отчёт о выполнении практической работы. Ответьте письменно на контрольные вопросы. Сделайте вывод.
6. Представьте отчёт о выполнении практической работы преподавателю на проверку.
Краткая теоретическая справка
Функция
F(х)
называется
первообразной
для функции f(х)
на
данном промежутке, если для любого х
из этого промежутка выполняется равенство
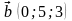 .
.
Основное свойство первообразных. Если функция F(х) есть первообразная для функции f(х) на данном промежутке, аС – произвольная постоянная, то функция F(х)+С также является первообразной для функции f(х).
Совокупность
всех первообразных данной функции f(х)
называется неопределенным интегралом
и обозначается
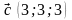 .
.
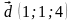
Свойства неопределенного интеграла:
1.
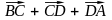 . 3.
. 3.
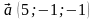 .
.
2.
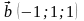 . 4.
. 4.
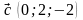 .
.
Интегрирование по частям — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция представима в виде произведения двух непрерывных и дифференцируемых функций, то справедлива следующая формула:
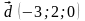 .
.
Предполагается,
что нахождение интеграла
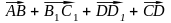 проще, чем
проще, чем
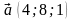 .
В противном случае применение метода
не оправдано.
.
В противном случае применение метода
не оправдано.
Практические задания
1. Найдите неопределенный интеграл методом непосредственного интегрирования.
2. Найдите неопределенный интеграл путем введения новой переменной.
3. Найдите неопределенный интеграл, используя формулу интегрирования по частям.
Для аудиторной работы
1.
а)
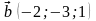 ; б)
; б)
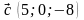 ;
в)
;
в)
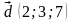 .
.
2.
а)
 ;
б)
.
;
б)
.
3.
а)
 ; б)
; б)
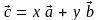 .
.
Для самостоятельной работы
Вариант 1
1. а) ; б) ; в) .
2.
а)
 ;
б)
;
б)
 .
.
3.
а)
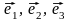 ; б)
; б)
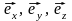 .
.
Вариант 2
1.
а)
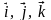 ; б)
; в)
; б)
; в)
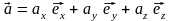 .
.
2.
а)
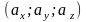 ;
б)
;
б)
 .
.
3.
а)
 ; б)
; б)
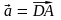 .
.
Вариант 3
1.
а)
 ; б)
; б)
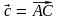 ; в)
; в)
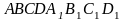 .
.
2.
а)
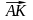 ;
б)
;
б)
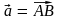 .
.
3.
а)
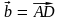 ; б)
; б)
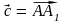 .
.
Вариант 4
1.
а)
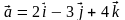 ; б)
; в)
; б)
; в)
 .
.
2. а) ; б) .
3.
а)
; б)
 .
.
4.
а)
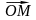 ; б)
; б)
 .
.
Требования к отчёту:
1. После выполнения работы студент обязан продемонстрировать преподавателю выполненные задания.
2. Предоставить отчёт о выполненной работе, содержащий:
- порядковый номер и наименование практической работы;
- цель практической работы;
- ход выполнения работы;
- ответы на контрольные вопросы.
Контрольные вопросы
1. Что называют первообразной функции?
2. Что такое неопределенный интеграл?
3. Перечислите свойства неопределенного интеграла.
3. В чем заключается метод непосредственного интегрирования?
4. В чем заключается метод замены переменной?
5. В чем заключается метод интегрирования по частям?
Сделайте вывод о том, какие математические навыки были приобретены вами в ходе выполнения данной практической работы.
Список рекомендуемой литературы:
1. Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика: Учебное пособие: В 2 кн. Кн. 2. – М.: «Издательство Новая Волна», 2009.
2. Лекции по математическому анализу, теории функций комплексного переменного и специальным функциям. - [Электронный ресурс] Режим доступа:
http://www.dmarsentev.narod.ru/kamenev.htm.
3. Мордкович А. Г. Алгебра и начала математического анализа. 10—11 классы. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (базовый уровень) / А. Г. Мордкович.— М.: Мнемозина, 2009.
4. Никольский С.М. Алгебра и начала анализа. 11 класс – М.: Просвещение, 2011.
5. http://uztest.ru – сайт подготовки к ЕГЭ.
6. http://ru.wikipedia.org – официальный сайт свободной энциклопедии Википедии.
