
- •Практическая работа № 30 Нахождение производных элементарных функций
- •Средства обучения:
- •Практическая работа № 31 Нахождение производной сложной функции
- •Средства обучения:
- •Практическая работа № 32 Применение производной первого порядка к исследованию функции на монотонность и экстремумы функции
- •Средства обучения:
- •Практическая работа № 33 Решение задач прикладного характера на нахождение наибольшего и наименьшего значения функции
- •Средства обучения:
- •Практическая работа № 34 Применение производной второго порядка к исследованию графика функции на выпуклость и перегиб
- •Средства обучения:
- •Практическая работа № 35 Построение графика функции с помощью производной
- •Средства обучения:
- •Практическая работа № 36 Нахождение неопределённого интеграла
- •Средства обучения:
- •Практическая работа № 37 Вычисление определённого интеграла. Решение задач физического и геометрического содержания с помощью определённого интеграла
- •Средства обучения:
- •Приложения определенного интеграла
- •1. Вычисление площади плоской фигуры.
- •2. Вычисление пути, пройденного точкой.
- •3. Вычисление работы силы.
- •Практическая работа № 38 Решение задач с использованием основных теорем стереометрии и вычислением угла между прямой и плоскостью
- •Средства обучения:
- •Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. Перпендикулярность прямой и плоскости
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 39 Решение задач на двугранный угол
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 40 Изображение пространственных фигур в стереометрии. Решение задач на вычисление площади ортогональной проекции фигуры
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 41 Построение развёртки призмы и параллелепипеда
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 42
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 43 Решение задач прикладного характера на вычисление площади поверхности тела с использованием знаний о призме
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 44 Построение развёртки пирамиды полной и усечённой
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 45 Вычисление площади боковой и полной поверхностей пирамиды полной и усечённой
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 46 Решение задач прикладного характера на вычисление площади поверхности тела с использованием знаний о пирамиде
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 47 Построение сечений куба, призмы и пирамиды
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 48 Построение развёрток правильных многогранников
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 49 Построение развёртки цилиндра
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 50 Построение развёртки конуса, усечённого конуса
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 51 Решение задач на нахождение основных элементов тел вращения
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 52 Решение задач по теме «Шар и сфера»
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 53 Вывод формул для вычисления объёмов параллелепипеда, призмы, цилиндра
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 54 Вывод формул для вычисления объёма пирамиды и конуса, объёма шара
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 55 Решение задач на вычисление объёмов геометрических тел
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 56 Вывод формул для вычисления площадей поверхностей тел вращения
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 57 Решение задач на вычисление площади поверхности тел вращения
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 58 Решение задач прикладного характера на вычисление объёмов и площадей поверхностей геометрических тел
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 59 Решение задач на составление уравнений прямой и плоскости в пространстве
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 60 Решение задач с использованием уравнения сферы
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 61 Действия над векторами в пространстве
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 62 Разложение вектора в пространстве. Нахождение координат вектора в заданном базисе
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 63 Решение задач на вычисление скалярного произведения двух векторов, использование свойств скалярного произведения, нахождение угла между векторами
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 64 Решение задач с использованием координатно-векторного метода
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 65 Решение комбинаторных задач
- •Средства обучения:
- •Практическая работа № 66 Формула бинома Ньютона
- •Средства обучения:
- •Практическая работа № 67 Решение задач на определение вероятности случайного события
- •Средства обучения:
- •9. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
Практическая работа № 34 Применение производной второго порядка к исследованию графика функции на выпуклость и перегиб
Цель: научиться применять производную второго порядка к исследованию графика функции на выпуклость и перегиб.
Место проведения: учебная аудитория, ОБОУ СПО «КЭМТ».
Средства обучения:
методические рекомендации к практической работе № 34.
Для выполнения задания необходимо:
знать:- определение производной функции первого и второго порядков;
- формулы и правила дифференцирования функций;
- определение точки перегиба функции;
- теорему о выпуклости функции.
уметь:- находить производные второго порядка;
- определять характер выпуклости с помощью второй производной;
- находить точки перегиба функции.
Рекомендации по выполнению заданий:
1. Повторите пройденный материал согласно требованиям к знаниям.
2. Прочтите краткую теоретическую справку.
3. Выполните с помощью преподавателя в случае необходимости практические задания для аудиторной работы, которые включают следующие виды работ:
нахождение производной первого и второго порядков;
определение характера выпуклости с помощью второй производной;
нахождение точек перегиба.
4. Выполните задания для самостоятельной работы в соответствии с вашим вариантом, пользуюсь алгоритмом выполнения аудиторных заданий.
5. Оформите отчёт о выполнении практической работы. Ответьте письменно на контрольные вопросы. Сделайте вывод.
6. Представьте отчёт о выполнении практической работы преподавателю на проверку.
Краткая теоретическая справка
Кривая
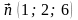 называется выпуклой
вниз (вверх)
в промежутке
называется выпуклой
вниз (вверх)
в промежутке
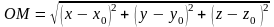 ,
если она лежит выше (ниже) касательной
в любой точке этого промежутка.
,
если она лежит выше (ниже) касательной
в любой точке этого промежутка.
Выпуклость
кривой, являющейся графиком функции
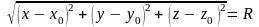 ,
характеризуется знаком её второй
производной: если
в некотором промежутке
,
характеризуется знаком её второй
производной: если
в некотором промежутке
 ,
то кривая выпукла вниз в этом промежутке;
если же
,
то кривая выпукла вниз в этом промежутке;
если же
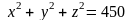 ,
то кривая выпукла вверх в этом промежутке.
,
то кривая выпукла вверх в этом промежутке.
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба.
Если
в точке перегиба x0
существует вторая производная f
''( x0
),
то
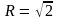 .
.
Теорема.
Пусть
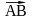 дифференцируема на промежутке
дифференцируема на промежутке
 .
Если во всех точках промежутка
.
Если во всех точках промежутка
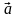 вторая производная функции y=f(x)
отрицательная, т.е.
вторая производная функции y=f(x)
отрицательная, т.е.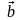 ,
то график функции на этом промежутке
выпуклый, если же
,
то график функции на этом промежутке
выпуклый, если же
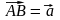 – вогнутый.
– вогнутый.
Практические задания
Найдите интервалы выпуклости и точки перегиба графика функции.
Для аудиторной работы
а)
 ; б)
; б)
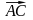 ; в)
; в)
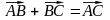 ; г)
; г)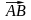 .
.
Для самостоятельной работы
Вариант 1
а)
; б)
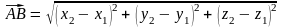 ; в)
; в)
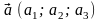 .
.
Вариант 2
а)
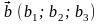 ; б)
; б)
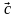 ; в)
; в)
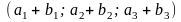 .
.
Вариант 3
а)
; б)
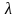 ; в)
; в)
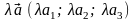 .
.
Вариант 4
а)
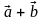 ; б)
; б)
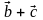 ; в)
; в)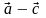
Требования к отчёту:
1. После выполнения работы студент обязан продемонстрировать преподавателю выполненные задания.
2. Предоставить отчёт о выполненной работе, содержащий:
- порядковый номер и наименование практической работы;
- цель практической работы;
- ход выполнения работы;
- ответы на контрольные вопросы.
Контрольные вопросы
1. Понятие выпуклости функции.
2. Понятие точки перегиба функции.
3. Как с помощью второй производной определить характер выпуклости функции.
Сделайте вывод о том, какие математические навыки были приобретены вами в ходе выполнения данной практической работы.
Список рекомендуемой литературы:
1. Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика: Учебное пособие: В 2 кн. Кн. 2. – М.: «Издательство Новая Волна», 2009.
2. Лекции по математическому анализу, теории функций комплексного переменного и специальным функциям. - [Электронный ресурс] Режим доступа:
http://www.dmarsentev.narod.ru/kamenev.htm.
3. Мордкович А. Г. Алгебра и начала математического анализа. 10—11 классы. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (базовый уровень) / А. Г. Мордкович.— М.: Мнемозина, 2009.
4. Никольский С.М. Алгебра и начала анализа. 11 класс – М.: Просвещение, 2011.
5. http://uztest.ru – сайт подготовки к ЕГЭ.
6. http://ru.wikipedia.org – официальный сайт свободной энциклопедии Википедии.
