
- •Практическая работа № 30 Нахождение производных элементарных функций
- •Средства обучения:
- •Практическая работа № 31 Нахождение производной сложной функции
- •Средства обучения:
- •Практическая работа № 32 Применение производной первого порядка к исследованию функции на монотонность и экстремумы функции
- •Средства обучения:
- •Практическая работа № 33 Решение задач прикладного характера на нахождение наибольшего и наименьшего значения функции
- •Средства обучения:
- •Практическая работа № 34 Применение производной второго порядка к исследованию графика функции на выпуклость и перегиб
- •Средства обучения:
- •Практическая работа № 35 Построение графика функции с помощью производной
- •Средства обучения:
- •Практическая работа № 36 Нахождение неопределённого интеграла
- •Средства обучения:
- •Практическая работа № 37 Вычисление определённого интеграла. Решение задач физического и геометрического содержания с помощью определённого интеграла
- •Средства обучения:
- •Приложения определенного интеграла
- •1. Вычисление площади плоской фигуры.
- •2. Вычисление пути, пройденного точкой.
- •3. Вычисление работы силы.
- •Практическая работа № 38 Решение задач с использованием основных теорем стереометрии и вычислением угла между прямой и плоскостью
- •Средства обучения:
- •Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. Перпендикулярность прямой и плоскости
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 39 Решение задач на двугранный угол
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 40 Изображение пространственных фигур в стереометрии. Решение задач на вычисление площади ортогональной проекции фигуры
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 41 Построение развёртки призмы и параллелепипеда
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 42
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 43 Решение задач прикладного характера на вычисление площади поверхности тела с использованием знаний о призме
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 44 Построение развёртки пирамиды полной и усечённой
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 45 Вычисление площади боковой и полной поверхностей пирамиды полной и усечённой
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 46 Решение задач прикладного характера на вычисление площади поверхности тела с использованием знаний о пирамиде
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 47 Построение сечений куба, призмы и пирамиды
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 48 Построение развёрток правильных многогранников
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 49 Построение развёртки цилиндра
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 50 Построение развёртки конуса, усечённого конуса
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 51 Решение задач на нахождение основных элементов тел вращения
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 52 Решение задач по теме «Шар и сфера»
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 53 Вывод формул для вычисления объёмов параллелепипеда, призмы, цилиндра
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 54 Вывод формул для вычисления объёма пирамиды и конуса, объёма шара
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 55 Решение задач на вычисление объёмов геометрических тел
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 56 Вывод формул для вычисления площадей поверхностей тел вращения
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 57 Решение задач на вычисление площади поверхности тел вращения
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 58 Решение задач прикладного характера на вычисление объёмов и площадей поверхностей геометрических тел
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 59 Решение задач на составление уравнений прямой и плоскости в пространстве
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 60 Решение задач с использованием уравнения сферы
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 61 Действия над векторами в пространстве
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 62 Разложение вектора в пространстве. Нахождение координат вектора в заданном базисе
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 63 Решение задач на вычисление скалярного произведения двух векторов, использование свойств скалярного произведения, нахождение угла между векторами
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 64 Решение задач с использованием координатно-векторного метода
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 65 Решение комбинаторных задач
- •Средства обучения:
- •Практическая работа № 66 Формула бинома Ньютона
- •Средства обучения:
- •Практическая работа № 67 Решение задач на определение вероятности случайного события
- •Средства обучения:
- •9. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
4. http://uztest.ru – сайт подготовки к ЕГЭ.
5. http://ru.wikipedia.org – официальный сайт свободной энциклопедии Википедии.
Практическая работа № 40 Изображение пространственных фигур в стереометрии. Решение задач на вычисление площади ортогональной проекции фигуры
Цель: научиться изображать пространственные фигуры в пространстве, вычислять площадь ортогональной проекции фигуры.
Место проведения: учебная аудитория, ОБОУ СПО «КЭМТ».
Средства обучения:
методические рекомендации к практической работе № 40.
Для выполнения задания необходимо:
знать:- определение параллельного проектирования;
- определение ортогонального проектирования;
- свойства параллельного проектирования;
- теорему о площади ортогональной проекции многоугольника.
уметь:- вычислять площадь ортогональной проекции многоугольника;
- выполнять построение изображений пространственных фигур.
Рекомендации по выполнению заданий:
1. Повторите пройденный материал согласно требованиям к знаниям.
2. Прочтите краткую теоретическую справку.
3. Выполните с помощью преподавателя в случае необходимости практические задания для аудиторной работы, которые включают следующие виды работ:
изображение пространственных фигур;
решение задач на вычисление площади ортогональной проекции.
4. Выполните задания для самостоятельной работы в соответствии с вашим вариантом, пользуюсь алгоритмом выполнения аудиторных заданий.
5. Оформите отчёт о выполнении практической работы. Ответьте письменно на контрольные вопросы. Сделайте вывод.
6. Представьте отчёт о выполнении практической работы преподавателю на проверку.
Краткая теоретическая справка
В стереометрии изучаются пространственные фигуры, которые на чертеже изображаются в виде плоских фигур. Для изображения пространственной фигуры на плоскости в геометрии обычно используется параллельное проектирование.
П усть
усть
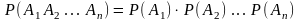 - некоторая плоскость, l
- пересекающая ее прямая (рис. 1). Через
произвольную точку A,
не принадлежащую прямойl,
проведем прямую, параллельную прямой
l.
Точка пересечения этой прямой с плоскостью
- некоторая плоскость, l
- пересекающая ее прямая (рис. 1). Через
произвольную точку A,
не принадлежащую прямойl,
проведем прямую, параллельную прямой
l.
Точка пересечения этой прямой с плоскостью
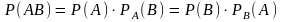 называется параллельной
проекцией
точки A
на плоскость
в
направлении прямой l. Обозначим ее A'.
Если точка A
принадлежит прямой l,
то параллельной проекцией A
на плоскость
считается точка пересечения прямой l
с плоскостью
.
называется параллельной
проекцией
точки A
на плоскость
в
направлении прямой l. Обозначим ее A'.
Если точка A
принадлежит прямой l,
то параллельной проекцией A
на плоскость
считается точка пересечения прямой l
с плоскостью
.
Свойства параллельного проектирования:
1. Если прямая параллельна или совпадает с прямой l, то ее проекцией в направлении этой прямой является точка. Если прямая не параллельна и не совпадает с прямой l, то ее проекцией является прямая.
2. Проекция отрезка при параллельном проектировании есть точка или отрезок, в зависимости от того лежит он на прямой, параллельной или совпадающей с прямой l, или нет. Параллельное проектирование сохраняет отношение длин отрезков, лежащих на прямой, не параллельной и не совпадающей с прямой l. В частности, при параллельном проектировании середина отрезка переходит в середину соответствующего отрезка.
3. Если две параллельные прямые не параллельны прямой l, то их проекции в направлении l могут быть или параллельными прямыми или одной прямой.
Параллельное проектирование, при котором проектирующие прямые перпендикулярны к плоскости проекций, называется ортогональным проектированием.
Теоремао площади ортогональной проекции многоугольника
Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции: Sпр = S cos φ.
Практические задания для аудиторной работы
1. Площадь плоского многоугольника равна 150 см2. Найдите площадь проекции этого многоугольника на плоскость, составляющую с плоскостью этого многоугольника угол 600.
2. Дан треугольник АВС со сторонамиа=13 см, b=14 см, с=15 см. Через сторону ВС проведена плоскость под углом 300 к плоскости . Найдите площадь проекции этого треугольника на плоскость .
3. Построить изображение куба при условии, что: а) одно из ребер параллельно направлению проектирования; б) одна из граней параллельна плоскости изображений; с) ни одно ребро не параллельно направлению проектирования.
Практические задания длясамостоятельной работы
Вариант 1
1. Найдите площадь плоского многоугольника, если площадь его проекции равна 20 м2 и двугранный угол между плоскостью многоугольника и плоскостью его проекции равен 450.
2. Гипотенуза прямоугольного треугольника равна m, а острый угол равен 600. Найдите площадь его проекции на плоскость, составляющую с плоскостью треугольника угол 300.
3. Изобразите в параллельной проекции правильную четырехугольную пирамиду.
Вариант 2
1. Найдите площадь проекции круга на плоскость, образующую с плоскостью круга угол 300. Радиус круга равен 2 м.
2. Стороны треугольника равны 3,9 см, 4,1 см и 2,8 см. Найдите площадь его проекции на плоскость, составляющую с плоскостью треугольника угол 600.
3. Постройте изображения прямого и наклонного параллелепипедов, две противоположные грани которых параллельны плоскости изображения.
Требования к отчёту:
1. После выполнения работы студент обязан продемонстрировать преподавателю выполненные задания.
2. Предоставить отчёт о выполненной работе, содержащий:
- порядковый номер и наименование практической работы;
- цель практической работы;
- ход выполнения работы;
- ответы на контрольные вопросы.
Контрольные вопросы
1. Что такое параллельное проектирование?
2. Какое проектирование называют ортогональным проектированием?
3. Справедливо ли утверждение: “Параллельные прямые проектируются в параллельные прямые или в одну прямую”?
4. Сформулировать основные свойства параллельного проектирования.
5. Как связаны площадь проектируемой фигуры с площадью её проекции при ортогональном проектировании?
Сделайте вывод о том, какие математические навыки были приобретены вами в ходе выполнения данной практической работы.
Список рекомендуемой литературы:
1. Геометрия, 10-11кл: Учеб.дляобщеобразоват. Учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Бутузов, С.Б. Кадомцев и др. – М.:Просвещение, 2001.
2. Учебное электронное пособие для основной школы издательства «Дрофа» - «Открытая математика 2.6. Стереометрия».
