
- •Практическая работа № 30 Нахождение производных элементарных функций
- •Средства обучения:
- •Практическая работа № 31 Нахождение производной сложной функции
- •Средства обучения:
- •Практическая работа № 32 Применение производной первого порядка к исследованию функции на монотонность и экстремумы функции
- •Средства обучения:
- •Практическая работа № 33 Решение задач прикладного характера на нахождение наибольшего и наименьшего значения функции
- •Средства обучения:
- •Практическая работа № 34 Применение производной второго порядка к исследованию графика функции на выпуклость и перегиб
- •Средства обучения:
- •Практическая работа № 35 Построение графика функции с помощью производной
- •Средства обучения:
- •Практическая работа № 36 Нахождение неопределённого интеграла
- •Средства обучения:
- •Практическая работа № 37 Вычисление определённого интеграла. Решение задач физического и геометрического содержания с помощью определённого интеграла
- •Средства обучения:
- •Приложения определенного интеграла
- •1. Вычисление площади плоской фигуры.
- •2. Вычисление пути, пройденного точкой.
- •3. Вычисление работы силы.
- •Практическая работа № 38 Решение задач с использованием основных теорем стереометрии и вычислением угла между прямой и плоскостью
- •Средства обучения:
- •Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. Перпендикулярность прямой и плоскости
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 39 Решение задач на двугранный угол
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 40 Изображение пространственных фигур в стереометрии. Решение задач на вычисление площади ортогональной проекции фигуры
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 41 Построение развёртки призмы и параллелепипеда
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 42
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 43 Решение задач прикладного характера на вычисление площади поверхности тела с использованием знаний о призме
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 44 Построение развёртки пирамиды полной и усечённой
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 45 Вычисление площади боковой и полной поверхностей пирамиды полной и усечённой
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 46 Решение задач прикладного характера на вычисление площади поверхности тела с использованием знаний о пирамиде
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 47 Построение сечений куба, призмы и пирамиды
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 48 Построение развёрток правильных многогранников
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 49 Построение развёртки цилиндра
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 50 Построение развёртки конуса, усечённого конуса
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 51 Решение задач на нахождение основных элементов тел вращения
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 52 Решение задач по теме «Шар и сфера»
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 53 Вывод формул для вычисления объёмов параллелепипеда, призмы, цилиндра
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 54 Вывод формул для вычисления объёма пирамиды и конуса, объёма шара
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 55 Решение задач на вычисление объёмов геометрических тел
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 56 Вывод формул для вычисления площадей поверхностей тел вращения
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 57 Решение задач на вычисление площади поверхности тел вращения
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 58 Решение задач прикладного характера на вычисление объёмов и площадей поверхностей геометрических тел
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 59 Решение задач на составление уравнений прямой и плоскости в пространстве
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 60 Решение задач с использованием уравнения сферы
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 61 Действия над векторами в пространстве
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 62 Разложение вектора в пространстве. Нахождение координат вектора в заданном базисе
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 63 Решение задач на вычисление скалярного произведения двух векторов, использование свойств скалярного произведения, нахождение угла между векторами
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 64 Решение задач с использованием координатно-векторного метода
- •Средства обучения:
- •3. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
- •Практическая работа № 65 Решение комбинаторных задач
- •Средства обучения:
- •Практическая работа № 66 Формула бинома Ньютона
- •Средства обучения:
- •Практическая работа № 67 Решение задач на определение вероятности случайного события
- •Средства обучения:
- •9. Электронный журнал "Прикладная геометрия". - [Электронный ресурс]Режим доступа: http://www.Mai.Ru/homelinks/apg/index.Htm.
ОГЛАВЛЕНИЕ
|
|
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА………………………………………. |
5 |
|
|
ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ РАБОТ………………………………. |
7 |
|
|
ПРАКТИЧЕСКИЕ РАБОТЫ…………………………………………... |
9 |
3.1. |
Нахождение производных элементарных функций…………………. |
9 |
3.2. |
Нахождение производной сложной функции………………………… |
11 |
3.3. |
Применение производной первого порядка к исследованию функции на монотонность и экстремумы функции………………………... |
14 |
3.4. |
Решение задач прикладного характера на нахождение наибольшего и наименьшего значения функции……………………………………. |
17 |
3.5. |
Применение производной второго порядка к исследованию графика функции на выпуклость и перегиб…………………………………. |
20 |
3.6. |
Построение графика функции с помощью производной……………. |
22 |
3.7. |
Нахождение неопределённого интеграла……………………………. |
25 |
3.8. |
Вычисление определённого интеграла. Решение задач физического и геометрического содержания с помощью определённого интеграла………………………………………………………………………… |
28 |
3.9. |
Решение задач с использованием основных теорем стереометрии и вычислением угла между прямой и плоскостью……………………. |
32 |
3.10. |
Решение задач на двугранный угол………………………………….. |
35 |
3.11. |
Изображение пространственных фигур в стереометрии. Решение задач на вычисление площади ортогональной проекции фигуры…. |
38 |
3.12. |
Построение развёртки призмы и параллелепипеда…………………. |
41 |
3.13. |
Вычисление площади боковой и полной поверхности призмы и параллелепипеда………………………………………………………….. |
43 |
3.14. |
Решение задач прикладного характера на вычисление площади поверхности тела с использованием знаний о призме…………………. |
45 |
3.15. |
Построение развёртки пирамиды полной и усечённой……………… |
47 |
3.16. |
Вычисление площади боковой и полной поверхности пирамиды полной и усечённой……………………………………………………. |
50 |
3.17. |
Решение задач прикладного характера на вычисление площади поверхности тела с использованием знаний о пирамиде……………… |
52 |
3.18. |
Построение сечений куба, призмы и пирамиды…………………….. |
54 |
3.19. |
Построение развёртки правильных многогранников………………... |
57 |
3.20. |
Построение развёртки цилиндра……………………………………… |
59 |
3.21. |
Построение развёртки конуса, усечённого конуса………………….. |
61 |
3.22. |
Решение задач на нахождение основных элементов тел вращения… |
64 |
3.23. |
Решение задач по теме «Шар и сфера»……………………………….. |
66 |
3.24. |
Вывод формул для вычисления объёмов параллелепипеда, призмы, цилиндра………………………………………………………………… |
69 |
3.25. |
Вывод формул для вычисления объёма пирамиды и конуса, объёма шара……………………………………………………………………... |
71 |
3.26. |
Решение задач на вычисление объёмов геометрических тел………. |
73 |
3.27. |
Вывод формул для вычисления площадей поверхностей тел вращения……………………………………………………………………….. |
75 |
3.28. |
Решение задач на вычисление площади поверхности тел вращения. |
78 |
3.29. |
Решение задач прикладного характера на вычисление объёмов и площадей поверхностей геометрических тел……………………….. |
80 |
3.30. |
Решение задач на составление уравнений прямой и плоскости в пространстве……………………………………………………………. |
83 |
3.31. |
Решение задач с использованием уравнения сферы………………… |
86 |
3.32. |
Действия над векторами в пространстве……………………………... |
88 |
3.33. |
Разложение вектора в пространстве. Нахождение координат вектора в заданном базисе…………………………………………………… |
91 |
3.34. |
Решение задач на вычисление скалярного произведения двух векторов, использование свойств скалярного произведения, нахождение угла между векторами…………………………………………….. |
94 |
3.35. |
Решение задач с использованием координатно-векторного метода.. |
97 |
3.36. |
Решение комбинаторных задач……………………………………….. |
99 |
3.37. |
Формула бинома Ньютона…………………………………………….. |
103 |
3.38. |
Решение задач на определение вероятности случайного события…. |
105 |
|
|
КРИТЕРИИ ОЦЕНКИ ПРАКТИЧЕСКИХ РАБОТ |
110 |
|
|
СПИСОК ЛИТЕРАТУРЫ |
111 |
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Учебная дисциплина «Математика» является естественнонаучной дисциплиной, обеспечивающей общеобразовательный уровень подготовки специалиста. Изучение дисциплины носит практико-ориентированный характер. Около пятидесяти процентов учебного времени отводится на практические занятия. Данная методическая разработка предназначена для проведения таких занятий.
Методические рекомендации по выполнению практических работ по учебной дисциплине «Математика» разработаны для студентов первого курса специальностей: 15.02.08 Технология машиностроения, 23.02.05 Эксплуатация транспортного электрооборудования и автоматики (по видам транспорта, за исключением водного), 13.02.11 Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям), 09.02.01 Компьютерные системы и комплексы, 15.02.06 Монтаж и техническая эксплуатация холодильно-компрессорных машин и установок
Задачей данной разработки является обеспечение условий для формирования практических навыков решения задач математического анализа, стереометрии, комбинаторики и теории вероятности.
Методическая разработка состоит из 38 практических работ, содержащих краткую теоретическую справку, задания для аудиторной и самостоятельной работ и контрольные вопросы. На выполнения работ отводится два или четыре аудиторных часа.
В ходе освоения учебной дисциплины «Математика» у обучающегося должно сформироватьсяпредставлениео математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики.
В результате выполнения практических работ обучающийся должен освоить основные методы дифференциального и интегрального исчислений, геометрии, комбинаторики, теории вероятностей и математической статистики.
Практические занятия обеспечивают условия для формирования практических умений и навыков:
- вычисления производных и дифференциалов, неопределенных и определенных интегралов;
- решения задач с использованием основных теорем стереометрии, задач прикладного характера на основе знаний о многогранниках и телах вращения;
- выполнение действий с векторами;
- решениякомбинаторных задач;
- решение простейших задач на определение вероятности случайных событий.
В ходе выполнения заданий обучающиеся приобретают нижеперечисленные умения и навыки, способствующие формированию общих и профессиональных компетенций:
- умение логически мыслить;
- умение планировать учебную деятельность с целью достижения прогнозируемого результата;
- умение осуществлять анализ собственной деятельности, самооценку и рефлексию;
- владение навыками работы с различными источниками информации;
- умение ориентироваться в информационных потоках, уметь выделять в них главное, необходимое.
При выполнения практических работ формируются универсальные учебные действия:
- личностные: оценивание усваиваемого содержания, исходя из социальных и личностных ценностей; овладение логическими действиями сравнения, анализа и синтеза, обобщения, развитие мотивов и понимания личностного смысла учения;
- регулятивные: целеполагание, планирование, прогнозирование, волевая саморегуляция, контроль, коррекция своих действий и оценка успешности усвоения;
- коммуникативные: планирование, умение точно выражать свои мысли, умение слышать, слушать и понимать собеседника; планировать и согласованно выполнять совместную деятельность; взаимно контролировать действия друг друга;
- познавательные: формулирование познавательной цели и внутреннего плана действий, поиск и выделение информации; подведение под понятие, выведение следствий, анализ; самостоятельное и групповое изучение материала, анализ, обобщение.
Методическая разработка может быть использована преподавателями и студентами других специальностей для выполнения практических работ.
ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ РАБОТ
№ п/п |
Наименование практической работы (тема) |
Количество аудиторных работ |
1 |
2 |
3 |
1 |
Нахождение производных элементарных функций. |
2 |
2 |
Нахождение производной сложной функции. |
2 |
3 |
Применение производной первого порядка к исследованию функции на монотонность и экстремумы функции. |
2 |
4 |
Решение задач прикладного характера на нахождение наибольшего и наименьшего значения функции. |
2 |
5 |
Применение производной второго порядка к исследованию графика функции на выпуклость и перегиб. |
2 |
6 |
Построение графика функции с помощью производной. |
2 |
7 |
Нахождение неопределённого интеграла. |
2 |
8 |
Вычисление определённого интеграла. Решение задач физического и геометрического содержания с помощью определённого интеграла. |
2 |
9 |
Решение задач с использованием основных теорем стереометрии и вычислением угла между прямой и плоскостью. |
2 |
10 |
Решение задач на двугранный угол. |
4 |
11 |
Изображение пространственных фигур в стереометрии. Решение задач на вычисление площади ортогональной проекции фигуры. |
2 |
12 |
Построение развёртки призмы и параллелепипеда. |
2 |
13 |
Вычисление площади боковой и полной поверхности призмы и параллелепипеда. |
2 |
14 |
Решение задач прикладного характера на вычисление площади поверхности тела с использованием знаний о призме. |
2 |
15 |
Построение развёртки пирамиды полной и усечённой. |
2 |
16 |
Вычисление площади боковой и полной поверхности пирамиды полной и усечённой. |
2 |
17 |
Решение задач прикладного характера на вычисление площади поверхности тела с использованием знаний о пирамиде. |
2 |
18 |
Построение сечений куба, призмы и пирамиды. |
4 |
19 |
Построение развёртки правильных многогранников. |
2 |
20 |
Построение развёртки цилиндра. |
2 |
21 |
Построение развёртки конуса, усечённого конуса.
|
2 |
1 |
2 |
3 |
22 |
Решение задач на нахождение основных элементов тел вращения. |
2 |
23 |
Решение задач по теме «Шар и сфера». |
2 |
24 |
Вывод формул для вычисления объёмов параллелепипеда, призмы, цилиндра. |
2 |
25 |
Вывод формул для вычисления объёма пирамиды и конуса, объёма шара. |
2 |
26 |
Решение задач на вычисление объёмов геометрических тел. |
2 |
27 |
Вывод формул для вычисления площадей поверхностей тел вращения. |
2 |
28 |
Решение задач на вычисление площади поверхности тел вращения. |
2 |
29 |
Решение задач прикладного характера на вычисление объёмов и площадей поверхностей геометрических тел. |
2 |
30 |
Решение задач на составление уравнений прямой и плоскости в пространстве. |
2 |
31 |
Решение задач с использованием уравнения сферы. |
2 |
32 |
Действия над векторами в пространстве. |
2 |
33 |
Разложение вектора в пространстве. Нахождение координат вектора в заданном базисе. |
2 |
34 |
Решение задач на вычисление скалярного произведения двух векторов, использование свойств скалярного произведения, нахождение угла между векторами |
2 |
35 |
Решение задач с использованием координатно-векторного метода |
2 |
36 |
Решение комбинаторных задач |
2 |
37 |
Формула бинома Ньютона |
2 |
38 |
Решение задач на определение вероятности случайного события |
2 |
Практическая работа № 30 Нахождение производных элементарных функций
Цель: научиться находить производные элементарных функций, применять правила дифференцирования.
Место проведения: учебная аудитория, ОБОУ СПО «КЭМТ».
Средства обучения:
методические рекомендации к практической работе № 30.
Для выполнения задания необходимо:
знать:- определение производной функции;
- формулы дифференцирования функций;
- правила дифференцирования функций.
уметь:- применять правила дифференцирования функций.
Рекомендации по выполнению заданий:
1. Повторите пройденный материал согласно требованиям к знаниям.
2. Прочтите краткую теоретическую справку.
3. Выполните с помощью преподавателя в случае необходимости практические задания для аудиторной работы, которые включают следующие виды работ:
применение формул и правил дифференцирования для нахождения производных элементарных функций.
4. Выполните задания для самостоятельной работы в соответствии с вашим вариантом, пользуюсь алгоритмом выполнения аудиторных заданий.
5. Оформите отчёт о выполнении практической работы. Ответьте письменно на контрольные вопросы. Сделайте вывод.
6. Представьте отчёт о выполнении практической работы преподавателю на проверку.
Краткая теоретическая справка
Производной
функции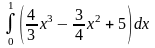 называется предел отношения приращения
функции
называется предел отношения приращения
функции
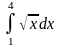 к
приращению аргумента
к
приращению аргумента
 ,
когда приращение аргумента
,
когда приращение аргумента
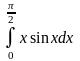 стремится
к нулю:
стремится
к нулю:
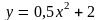 .
.
Нахождение производной функции называют дифференцированием.
Основные правила дифференцирования:
1. Производная суммы или разности функций:
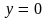 .
.
2. Производная произведения постоянной на функцию:
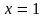 ,
,
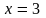 .
.
3. Производная произведения двух функций:
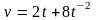 .
.
4. Производная частного (дроби):
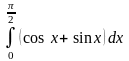 .
.
Практические задания
1.Найти производную функции.
2. Найти значение производной функции в данной точке.
3.
Вычислить скорость изменения функции
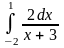 в точке
в точке
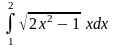 .
.
Для аудиторной работы
1.
а)
 ; б)
; б)
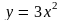 ; в)
.
; в)
.
2.
а)
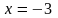 ;
б)
;
б)
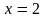 .
.
3.
 . 4.
. 4.
 .
.
Для самостоятельной работы
Вариант 1
1.
а) ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)
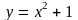 ;
д)
.
;
д)
.
2.
а) ;
б)
.
;
б)
.
3.
а)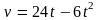 ; б)
; б) .
.
Вариант 2
1.
а)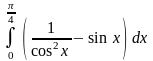 ;б)
;б)
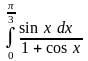 ;
в)
;
в)
 ;
г)
;
г)
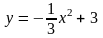 ;
д)
.
;
д)
.
2.
а)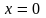 ;
б)
.
;
б)
.
3.
а)
 ; б)
; б)
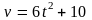 .
.
Вариант 3
1.
а)
 ;
б)
;
б) ;
в)
;
г)
;
д)
.
;
в)
;
г)
;
д)
.
2.
а)
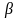 ;
б)
;
б)
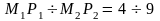 .
.
3.
а)
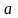 ; б)
; б)
 .
.
Вариант 4
1.
а)
;
б)
;
в)
; г)
 ; д)
.
; д)
.
2.
а)
;
б)
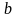 .
.
3.
а)
; б)
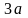 .
.
Требования к отчёту:
1. После выполнения работы студент обязан продемонстрировать преподавателю выполненные задания 1-3.
2. Предоставить отчёт о выполненной работе, содержащий:
- порядковый номер и наименование практической работы;
- цель практической работы;
- ход выполнения работы;
- ответы на контрольные вопросы.
Контрольные вопросы
1. Что называют производной функции?
2. Какие основные правила дифференцирования вы знаете?
Сделайте вывод о том, какие математические навыки были приобретены вами в ходе выполнения данной практической работы.
Список рекомендуемой литературы:
1. Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика: Учебное пособие: В 2 кн. Кн. 2. – М.: «Издательство Новая Волна», 2009.
2. Лекции по математическому анализу, теории функций комплексного переменного и специальным функциям. - [Электронный ресурс] Режим доступа:
http://www.dmarsentev.narod.ru/kamenev.htm.
3.Мордкович А. Г. Алгебра и начала математического анализа. 10—11 классы. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (базовый уровень) / А. Г. Мордкович.— М.: Мнемозина, 2009.
4. Никольский С.М. Алгебра и начала анализа. 11 класс – М.: Просвещение, 2011.
5. http://uztest.ru – сайт подготовки к ЕГЭ.
6. http://ru.wikipedia.org – официальный сайт свободной энциклопедии Википедии.
