Диаграммы прохождения сигналов

При решении задач поиска дефектов обычно учитываются структурные особенности и внутренние связи в объекте, для чего удобно использовать графоаналитические модели объекта в виде диаграмм прохождения сигналов.

Графическое изображение диаграмм прохождения сигналов представляют собой схему, состоящую из узлов, соединенных направленными ветвями. Диаграмме, как правило, соответствуют переменные (ветви характеризуют связь между переменными); их операторам – коэффициенты уравнений.

В ряде случаев диаграмма прохождения сигналов может быть построена без составления уравнений, только на основании рассмотрения структуры объекта.

Узлами диаграммы могут быть источники, простые каскадные узлы и стоки.

Источники – это такие узлы, у которых имеются только выходящие ветви; стоки – только входящие ветви. Источники соответствуют независимыми переменным, а стоки – зависимым. Узлы с входящими и выходящими ветвями являются простыми каскадными узлами.

Каждой ветви соответствует свой оператор 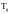, где i – узел откуда начинается ветвь, j – узел, где ветвь заканчивается.

Направление ветви указывают стрелкой. Каждому узлу соответствует своя переменная, равная сумме входящих в узел сигналов:

,

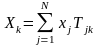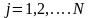
Каждый входящий сигнал равен произведению оператора входящей ветви на сигнал узла, из которого ветвь выходит.

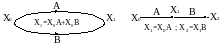
Рисунок 3 – Диаграммы прохождения сигналов

Топологические модели

Топологической моделью объекта называют ориентированный граф, вершинами которого, являются свойства объекта, или характеризующие эти свойства параметры. Вершинами графа могут быть также существенные свойства или параметры внешней среды.

Структурные параметры – это параметры, характеризующие свойство или функционирование отдельных составных частей объекта, в модели им соответствуют возможные дефекты, вызывающие нарушение свойств или нормальное функционирование составных частей. Структурные параметры и соответствующие им дефекты обозначаются одними и теми же символами 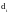, i=1,2,…,n. Эти параметры в модели являются входными вершинами графа (вершинами, не имеющими заходящих дуг, ведущих от других вершин). Другие параметры модели называемые косвенными, обозначаются 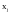, j=1,2,3,…,n. Эти параметры являются внутренними вершинами графа (рисунок 3).

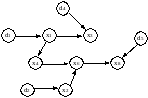
Рисунок 3 – Топологическая модель объекта

Каждой вершине или графа соответствует число – вес вершины или , который характеризует затраты на оценку соответствующих параметров (время, стоимость, доступность для измерения) и достоверность оценки. Если оценка параметра непосредственно невозможна, или не может быть осуществлена без разборки объекта, то вес вершины принимается равным нулю,.

Дуги (ветви) графа представляют причинно – следственные связи между параметрами. Каждой дуге графа ставится в соответствие число – вес дуги 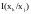, представляющий собой относительное количество информации о значении параметра . Значение этого параметра, соответствующего начальной вершине дуги, получают в результате оценки параметра , в свою очередь соответствующего конечной вершине дуги. Веса дуг (петель) одинаковы и равны некоторой максимальной величине: 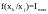, т.е. максимум информации о значении параметра может быть получен при оценке самого параметра.

Для удобства расчетов целесообразно перейти от абсолютных весов вершин и дуг к их относительным весам соответственно:

;

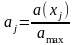где – максимальный абсолютный вес некоторой вершины.

Т.к. данные для расчета количества информации обычно отсутствуют, то для оценки весов дуг могут использоваться мнения экспертов.