11. Типическая, серийная, собственно-случайная и механическая выборки.

В теории выборочного методаразработаны раз–личные способы отбора и виды выборки, обеспечивающие репрезентативность. Под способом отбора понимают порядок отбора единиц из генеральной совокупности. Различают два способа отбора: повторный и бесповторный. При повторном отборе каждая отобранная в случайном порядке единица после ее об–следования возвращается в генеральную совокупность и при последующем отборе может снова попасть в выборку. Этот способ отбора построен по схеме «возвращенного шара». При таком способе отбора вероятность попасть в выборку для каждой единицы генеральной совокупности не меняется независимо от числа отбираемых единиц. При бесповторном отборе каждая единица, отобранная в случайном порядке, после ее обследования в генеральную совокупность не возвращается. Этот способ отбора построен по схеме «невозвращенного шара». Вероятность попасть в выборку для каждой единицы генеральной совокупности увеличивается по мере производства отбора.

Генеральная совокупность– вся изучаемая выборочными методами статистическая совокупность объектов и/или явлений общественной жизни, имеющих общие качественный признаки или количественные перемены.

Выборочная совокупность – часть объектов из генеральной совокупности, отобранных для изучениия, с тем чтобы сделать заключение о всей генеральной совокупности. Для того чтобы заключение, полученное путем изучения выборки, можно было распространить на всю генеральную совокупность, выборка должна обладать свойством репрезентативности.

В зависимости от методики формирования выборочной совокупности различают следующие основные виды выборки: собственно случайная, механическая, типическая (стратифицированная, районированная), серийная (гнездовая).

Выборка называется собственно случайной, если при извлечении выборки объема все возможные комбинации из элементов, которые могут быть получены из генеральной совокупности объема, имеют равную вероятность быть извлеченными.

Собственно случайная выборка формируется в строгом соответствии с научными принципами и правилами случайного отбора. Для получения собственно случайной выборки генеральная совокупность строго подразделяется на единицы отбора, и затем в случайном повторном или бесповторном порядке отбирается достаточное число единиц. Случайный порядок – это порядок, равносильный жеребьевке. На практике такой порядок лучшим образом обеспечивается при использовании специальных таблиц случайных чисел.

При бесповторном способе отбора расчет стандартной ошибки осуществляется с помощью формулы:

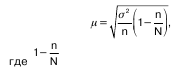
—доля единиц генеральной совокупности, не попавших в выборку.

Формировать выборку в строгом соответствии с правилами случайного отбора практически очень сложно, а иногда невозможно, так как при использовании таблиц случайных чисел необходимо пронумеровать все единицы генеральной совокупности.

При чисто механической выборкевся генеральная совокупность единиц должна быть прежде всего представлена в виде списка единиц отбора, составленного в каком-то нейтральном по отношению к изучаемому признаку порядке. Затем список единиц отбора разбивается на столько равных частей, сколь–ко необходимо отобрать единиц. Далее по заранее установленному правилу, не связанному с вариацией исследуемого признака, из каждой части списка отбирается одна единица. Этот вид выборки не всегда может обеспечить случайный характер отбора, и полученная выборка может оказаться смещенной. Объясняется это тем, что, во-первых, упорядочение единиц генеральной совокупности может иметь элемент неслучайного характера. Во-вторых, отбор из каждой части генеральной совокупности при неправильном установлении начала отсчета может также привести к ошибке смещения.Типическая (районированная, стратифицированная) выборкапреследует две цели:

1) обеспечить представительство в выборке соответствующих типических групп генеральной совокупности по интересующим исследователя признакам;

2) увеличить точность результатов выборочного об–следования.

При типической выборке до начала ее формирования генеральная совокупность единиц разбивается на типические группы. При этом очень важным моментом является правильный выбор группировочного признака. Выделенные типические группы могут со–держать одинаковое или различное число единиц от–бора. В первом случае выборочная совокупность формируется с одинаковой долей отбора из каждой группы, во втором – с долей, пропорциональной ее доле в генеральной совокупности. Если выборка формируется с равной долей отбора, по существу она равносильна ряду собственно случайных выборок из меньших генеральных совокупностей, каждая из которых и есть типическая группа. Отбор из каждой группы осуществляется в случайном (повторном или бесповторном) либо механическом порядке. При типической выборке удается устранить влияние меж–групповой вариации изучаемого признака на точность ее результатов, так как обеспечивается обязательное представительство в выборочной совокупности каждой из типических групп. Стандартная ошибка выборки будет зависеть от величины средней из групповых дисперсий.

Поскольку средняя из групповых дисперсий всегда меньше общей дисперсии, постольку при прочих равных условиях стандартная ошибка типической выборки будет меньше стандартной ошибки собственно случайной выборки.

При определении стандартных ошибок типической выборки применяются следующие формулы:

1. при повторном способе отбора:

2) при бесповторном способе отбора:

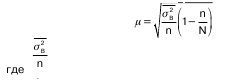
– средняя из групповых дисперсий в выборочной совокупности

Серийная (гнездовая) выборка– это такой вид формирования выборочной совокупности, когда в случайном порядке отбираются не единицы, подлежащие обследованию, а группы единиц (серии, гнезда). Внутри отобранных серий (гнезд) обследованию подвергаются все единицы. Серийную выборку практически организовать и провести легче, чем отбор отдельных единиц. Однако при этом виде выборки, во-первых, не обеспечивается представительство каждой из серий, и, во-вторых, не устраняется влияние межсерийной вариации изучаемого признака на результаты обследования. В том случае, когда эта вариация значительна, она приведет к увеличению случайной ошибки репрезентативности. При выборе вида выборки исследователю необходимо учитывать это обстоятельство.

Стандартная ошибка серийной выборки определяется по формулам:

1. при повторном способе отбора:

– межсерийная дисперсия выборочной совокупности;

r – число отобранных серий;

2. при бесповторном способе отбора:

3. 

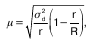
где R – число серий в генеральной совокупности.

12.Структурные средние.

Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:

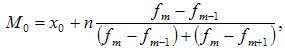
где:

• значение моды

• нижняя граница модального интервала

• величина интервала

• частота модального интервала

—частота интервала, предшествующего модальному

• частота интервала, следующего за модальным

Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.

Медианой называется вариант, расположенный в центре ранжированного ряда. Медиана делит ряд на две равные части таким образом, что по обе стороны от нее находится одинаковое количество единиц совокупности. При этом у одной половины единиц совокупности значение варьирующего признака меньше медианы, у другой – больше.

Описательный характер медианы проявляется в том, что она характеризует количественную границу значений варьирующего признака, которыми обладает половина единиц совокупности.

Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот , а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле:

Ме = (n(число признаков в совокупности) + 1)/2,

в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).

При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:

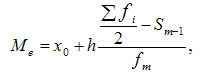
где:

• искомая медиана

• н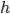ижняя граница интервала, который содержит медиану

• величина интервала

• сумма частот или число членов ряда

• сумма накопленных частот интервалов, предшествующих медианному

• частота медианного интервала

Медиана и мода в отличие от средней арифметической не погашают индивидуальных различий в значениях варьирующего признака и поэтому являются дополнительными и очень важными характеристиками статистической совокупности. На практике они часто используются вместо средней либо наряду с ней. Особенно целесообразно вычислять медиану и моду в тех случаях, когда изучаемая совокупность содержит некоторое количество единиц с очень большим или очень малым значением варьирующего признака.

13.Нормальное распределение. Методика расчета теоретических частот нормального распределения. Критерии согласия, их виды и формулы.

Существует ряд критериев согласия. Чаще применяют критерии Пирсона, Романовского и Колмогорова.

Критерий согласия Пирсона

Критерий χ2 (критерий согласия Пирсона) — характеристика распределения, используемая для проверки статистических гипотез. Под статистическим критерием подразумевается правило, обеспечивающее с определенной вероятностью принятие истинной или отклонение ложной гипотезы. В качестве критериев в математической статистике применяют определенные случайные величины, являющиеся функциями изучаемых случайных величин и чисел степеней свободы.

• один из основных:

где k – число групп, на которые разбито эмпирическое распределение,

• наблюдаемая частота признака в i-й группе,

• теоретическая частота

При полном совпадении эмпирических и ожидаемых частот ( f – f ')=0, в противном случае x^2=0.

Если x^2 рассчитанное, больше табличного, то x^2 рассчитанное > x^2i, при заданном уровне значимости альфа и числа степеней свободы гипотезу о случайном расхождении откланяют. Если x^2 рассчитанное <= X табличного , то эмпирический ряд хорошо согласуют с гипотезой о предпологаемом распределении и с вероятностью 1- ɑ можно утверждать что расхождения между теоретическими и эмпирическими частотами случайны.

К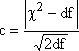ритерий Романовского с основан на использовании критерия Пирсона, т.е. уже найденных значений

, и числа степеней свободы df:

Он удобен при отсутствии таблиц для

Если с<3, то расхождения распределений случайны, если же с>3, то не случайны и теоретическое распределение не может служить моделью для изучаемого эмпирического распределения.

Критерий Колмогорова l основан на определении максимального расхождения между накопленными частотами и частостями эмпирических и теоретических распределений:

или

где D и d – соответственно максимальная разность между накопленными частотами

и накопленными частостями

эмпирического и теоретического рядов распределений;

N – число единиц совокупности.

Основное условие использования критерия Колмогорова – достаточно большое число наблюдений.

Кривая нормального распределения.

Закон нормального распределения:

у – ордината нормального распределения

t – нормированное отклонение.

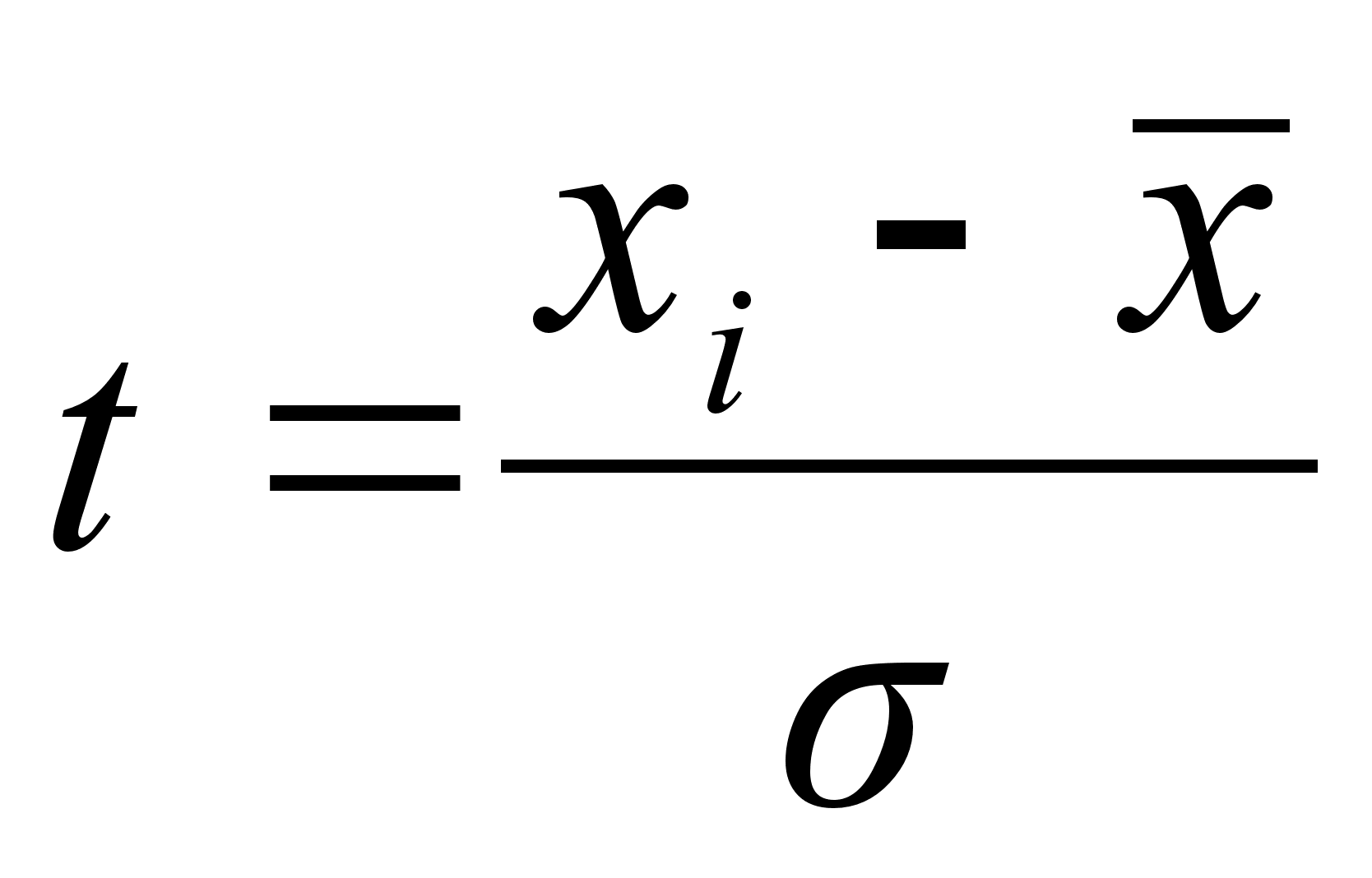
е=2,7218; xi – варианты вариационного ряда;

- среднее;

Свойства:

Функция нормального распределения – четная, т.е. f(t)=f(-t),

Функция нормального распределения полностью определяется

и СКО.

Проверка гипотезы о нормальном распределении.

Причиной частого обращения к закону распределения является то, что зависимость возникающая в результате действия множества случайных причин ни одна из которых не является преобладающей. Если в вариационном ряду рассчитали Мо=Ме, то это может указывать на близость к нормальному распределению. Наиболее точная проверка соответствия нормальному закону производится с помощью специальных критериев.

Методика расчета теоретических частот.

1.Определяется среднее арифметическое и по интервальному вариационному ряду, считается t по каждому интервалу.

2.Находим значение плотности вероятности для нормированного закона распределения.

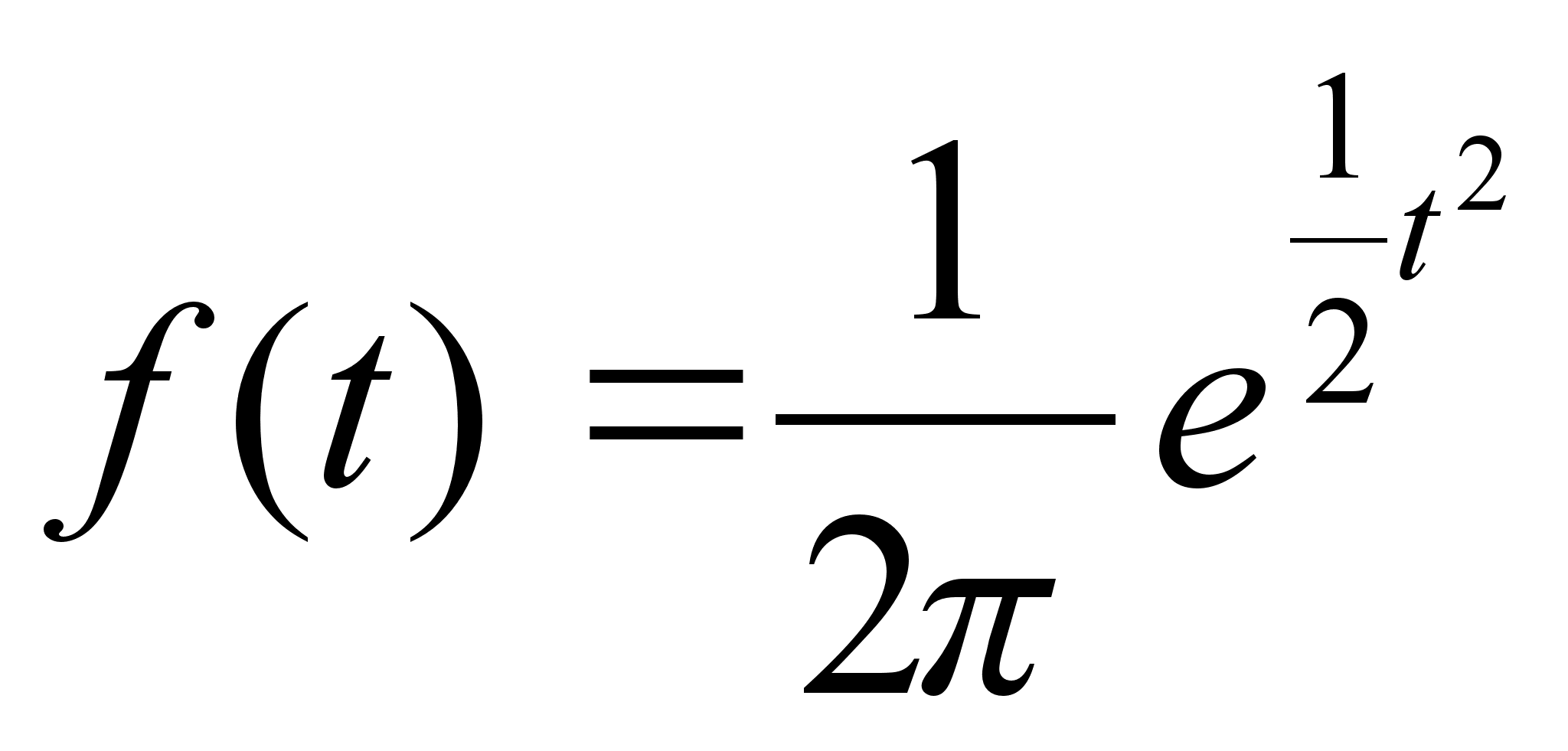
3.Находим теоретическую частоту

l – длина интервала

• сумма эмпирических частот

• плотность вероятности

4.Расчет коэффициента Пирсона

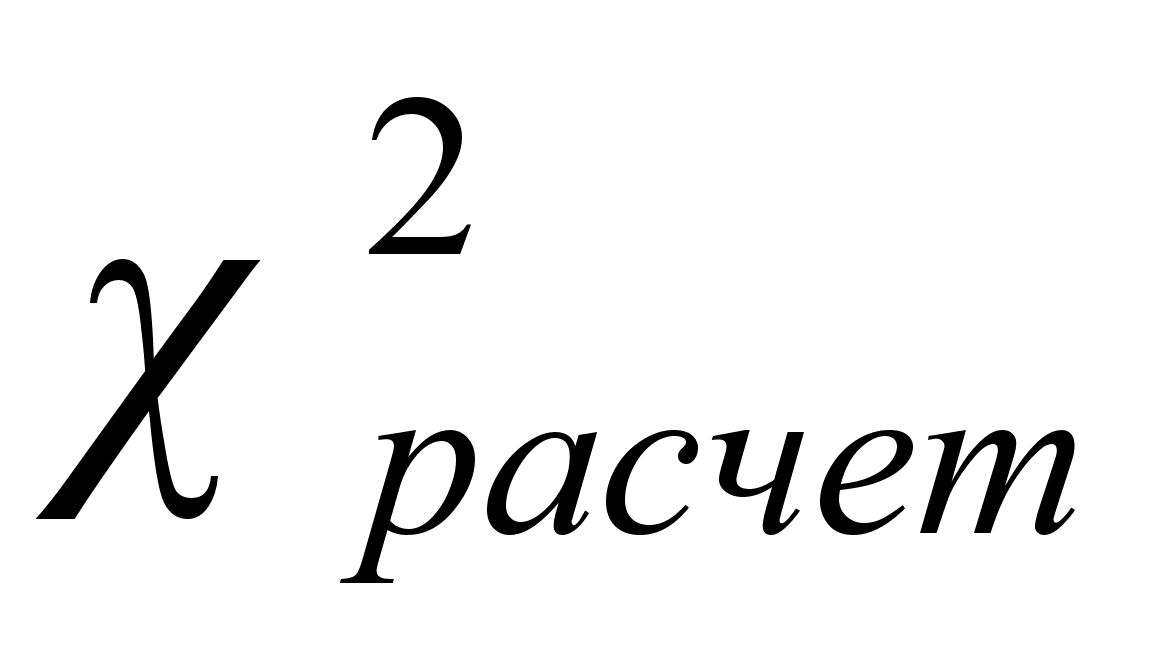
5.табличное значение

d.f. – количество интервалов – 3

d.f. – количество степеней свободы.

6.если

>

то распределение не является нормальным, т.е. гипотеза о нормальном распределении отменяется. Если

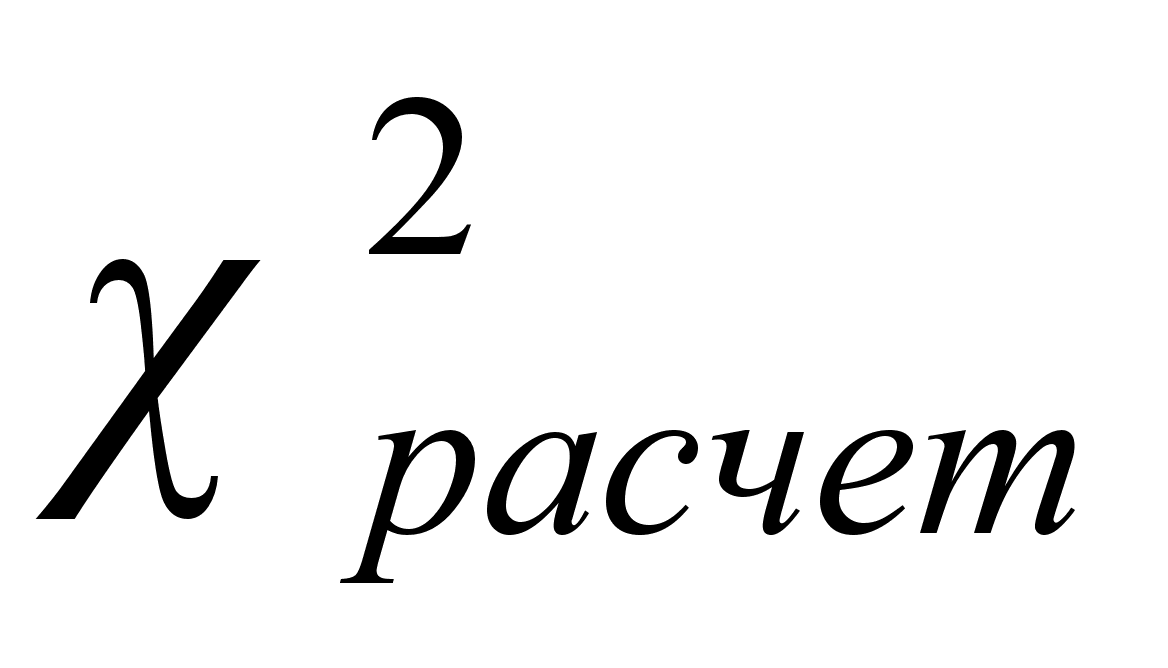
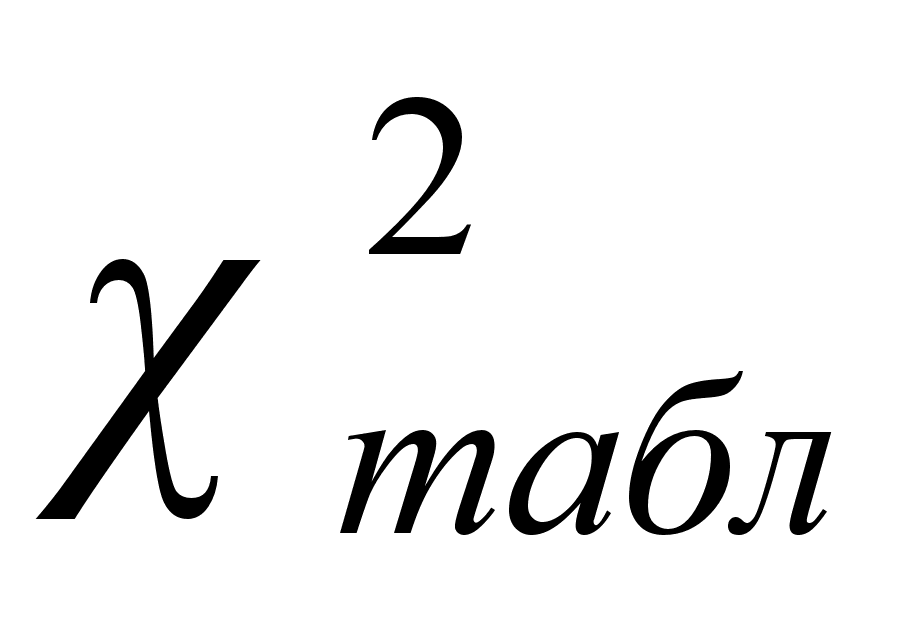то распределение является нормальным.