16.Парная линейная и нелинейная зависимости.

17.Множественная корреляция.

КОРРЕЛЯЦИЯ МНОЖЕСТВЕННАЯ - корреляция между переменной зависимой у и набором переменных независимых x1,x2,...,xk в уравнении регрессии линейной множественной y = ∑bixi + a. Квадрат коэффициента множественной корреляции R² является мерой совместного влияния всех независимых переменных (предикторов) на зависимую, долей объясненной дисперсии зависимой переменной. Если предикторы не коррелируют друг с другом, их общее влияние на зависимую переменную может быть определено как сумма влияний каждого из них, взятого в отдельности. Однако в абсолютном большинстве случаев наблюдается эффект интеркорреляции , а иногда даже мультиколлинеарности , что делает прямой подход к измерению К.М. невозможным.

Коэффициент К.М. вычисляется по формуле:

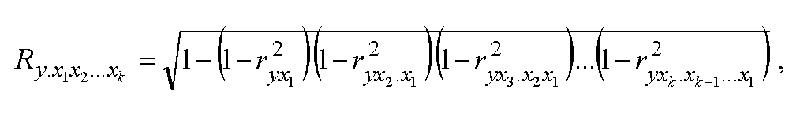
где ryx1 - коэффициент линейной корреляции Пирсона между переменными y и x1;

ryx2.x1 - коэффициент частной корреляции первого порядка между переменными у и х2 при устраненном влиянии переменной х1;

ryx3.x2x1 - коэффициент частной корреляции второго порядка между переменными у и х3 при устраненном влиянии переменных х1 и х2.

и т.п.

Если все коэффициенты корреляции между независимыми переменными rij = 0, то формула коэффициента К.М. принимает вид:

Изучение связи между результативным и двумя или более факторными признаками называется множественной регрессией. При исследовании зависимостей методами множественной регрессии ставят 2 задачи.

1.определение аналитического выражения связи между результативным признаком у и фактическими признаками х1, х2, х3, …хк, т.е. найти функцию у=f(х1, х2, …хк)

2.Оценка тесноты связи между результативным и каждым из факторных признаков.

Корреляционно-регрессионная модель (КРМ) – такое уравнение регрессии, которое включает основные факторы, влияющие на вариацию результативного признака.

Построение модели множественной регрессии включает этапы:

-выбор формы связи

-отбор факторных признаков

-обеспечение достаточного объема совокупности для получения верных оценок.

все множество связей между переменными, встречающиеся на практике достаточно полно описывается функциями 5-ти видов:

●линейная:

●степенная:

●показательная:

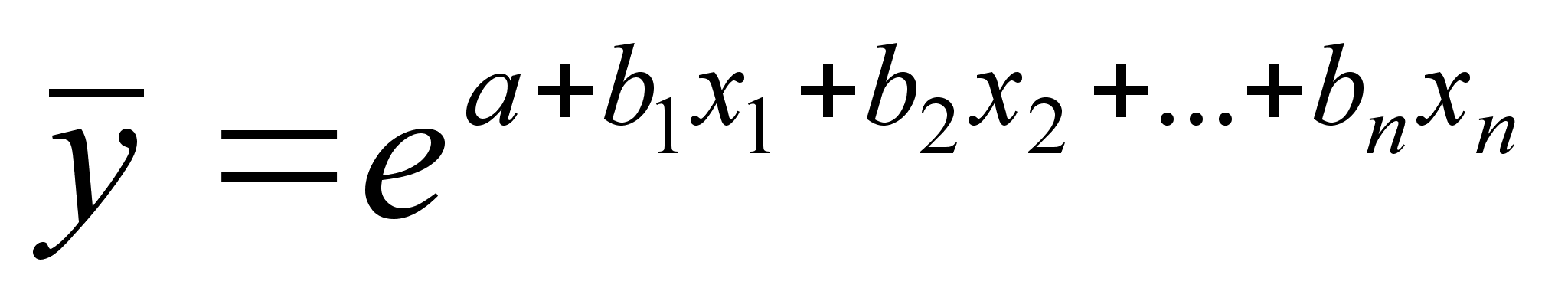
●парабола:

●гипербола:

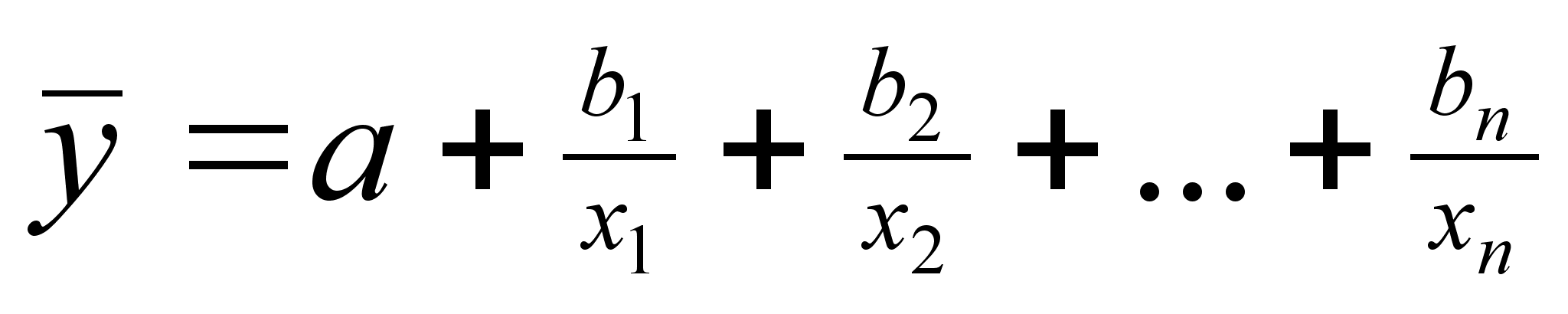
хотя все 5 функций присутствуют в практике КРА, наиболее часто используется линейная зависимость, как наиболее простая и легко поддающаяся интерпретации уравнение линейной зависимости: к – множество факторов включающихся в уравнение, bj – коэффициент условно-чистой регрессии, который показывает среднее по совокупности отклонение результативного признака от его среднего значения при отклонении фактора xj от своей средней величины на единицу при условии, что все остальные факторы, входящие в уравнение сохраняют средние значения.

Отбор факторов для включения в уравнение множественной регрессии:

между результативным и фактическим признаками должна быть причинно-следственная зависимость.

результативный и фактический признаки должны быть тесно связаны между собой иначе возникает явление мультиколлинеарности (>06), т.е. включенные в уравнение факторные признаки влияют не только на результативный, но друг на друга, что влечет к неверной интерпретации числовых данных.

Методы отбора факторов для включения в уравнение множественной регрессии:

экспертный метод – основан на интуитивно логическом анализе который выполняется высококвалифицированными экспертами.

использование матриц парных коэффициентов корреляции осуществляется параллельно с первым методом, матрица симметрична относительно единичной диагонали.

пошаговый регрессионный анализ – последовательное включение факторных признаков в уравнение регрессии и проверки значимости проводится на основании значений двух показателей на каждом шаге. Показатель корреляции, регрессии.

Показатель корреляции: рассчитывают изменение теоретической корреляции отношения или изменение средней остаточной дисперсии. Показатель регрессии – изменение коэффициента условно чистой регрессии.