ХВИЛЕЮ називають процес поширення коливань, який супроводжується перенесенням енергії від джерела в навколишній простір.

Величезний рух хвиль на поверхні океану, звук, світло, ударна хвиля від надзвукового літака – все це хвилі.

Найчастіше зустрічаються хвилі, породжені гармонічним джерелом. Наприклад від камертона, який здійснює гармонічні коливання сталої частоти. Це поширюються в повітрі звукові гармонічні хвилі. При цьому частинки повітря здійснюють гармонічні коливання біля положень рівноваги. В світловій (електромагнітній) хвилі коливання здійснюють вектори напруженості електричного і магнітного полів. Існують два типи хвиль: механічні хвилі, які поширюються у пружному середовищі та електромагнітні.

Характеристики хвиль різного походження, звичайно, однакові, але існують і деякі відмінності.

Механічні хвилі

ЗАГАЛЬНІ ПОЛОЖЕННЯ

Процес поширення коливань в пружному середовищі називають механічною хвилею. Розглянемо схему виникнення одновимірної пружної хвилі . Нехай вздовж осі х розміщений ланцюжок ма­теріальних точок, кожна масою т, зв’язаних між собою силами. Умовно ці сили зображені у вигляді пружинок між частинками. Якщо частинку, яка стоїть на початку ланцюжка, почати зміщувати вгору, то сусідні частинки також почнуть зміщуватись угору, їх потягнуть пружинки. Але існує інер­ція, і тому зміщення частинок будуть запізнюватись.

Коли перша частинка досягне максимального відхилення від поло­ження рівноваги, останні найближчі частинки відхиляться на меншу відстань, а до частинок, розміщених далі, вплив взагалі не дійде, і вони залишаться на своїх місцях.

Легко зрозуміти, що якщо перша частинка здійснює гармонічні ко­ливання, то й останні частинки з часом втягнуться в цей процес.

Енергію для коливань вони будуть отримувати по ланцюжку від першої частинки, яку називають ДЖЕРЕЛОМ ХВИЛІ.

Хвильовий процес в середовищі – це процес перенесення енергії у просторі без переносу маси.

Енергія послідовно передається від однієї частинки до іншої. Оскільки енергія на цьому шляху не втрачається, то кожна частинка почне здійснювати коливання з тією самою амплітудою, що й перша ча­стинка — джерело, і з тією самою частотою, Різниця тільки в тому, що коливання різних частинок здійс­нюватиметься в різних фазах.

Істотно, що частинки середовища не переносяться хвилею, а лише здійснюють гармонічні коливання біля положень рівноваги. Переноситься тільки енергія.

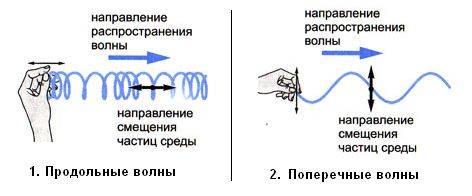
Розрізняють хвилі ПОПЕРЕЧНІ і ПОВЗДОВЖНІ.

У повздовжній хвилі напрям коливань збігається з напрямом поширення хвилі. У поперечній хвилі напрям коливань перпендикулярний до напряму поширення хвилі. (див. рисунок).

Повздовжні хвилі розповсюджуються в усіх тілах: газоподібних, рідких і твердих.

Поперечні пружні хвилі розповсюджуються тільки в твердих тілах, де є зсувна пружність.

ХАРАКТЕРИСТИКИ МОНОХРОМАТИЧНОЇ ХВИЛІ

ЧАСТОТА ХВИЛІ ;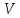

ЦИКЛІЧНА ЧАСТОТА ХВИЛІ ;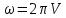

ПЕРІОД КОЛИВАНЬ ХВИЛІ ;

АМПЛІТУДА ХВИЛІ ;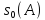

ФАЗОВА ШВИДКІСТЬ ;

ДОВЖИНА ХВИЛІ 𝝀;

ХВИЛЬОВИЙ ВЕКТОР

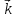
Значення величин, які характеризують коливання частинок 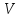, , 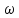Т, 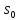, нам уже знайоме. Перейдемо до розгляду останніх.

ФАЗОВОЮ ШВИДКІСТЮ хвилі називають швидкість з якою рухаються точки хвилі з однаковою фазою.

Фазова швидкість визначається властивостями середовища, а саме: пружними й інерціальними влас­тивостями, Чим вища пружність, тим швидше «підтягуються» сусідні частинки. Чим більша густина, тобто маса частинок, тим більша інерція і тим більше запізнювання.

Таким чином, фазова швидкість визначається відношенням сил пружності до сил інерції. Для поздов­жніх хвиль у твердому тілі фазова швидкість визначається за формулою

,

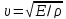де Е — модуль повздовжньої пружності, або модуль Юнга; ρ — густина середовища.

Не слід плутати фазову швидкість зі швидкістю коливань частинки, яка весь час змінюється і дорівнює першій похідній від зміщення за часом.

ДОВЖИНА ХВИЛІ — відстань, на яку поширюється фаза коливань за час, що дорівнює одному періоду коливань.

Оскільки фаза переміщується зі швидкістю 𝛖, то

.

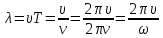Із формули видно, що частинки, які містяться одна від одної на відстані, що дорівнює довжині хвилі, коливаються в одній фазі. Точніше, різниця фаз дорівнює 2. Тому можна також дати інше означення:

Довжиною хвилі називають відстань між найближчими частинками, які здійснюють коливання, в однаковій фазі.

ХВИЛЬОВОЮ ПОВЕРХНЕЮ називають геометричне місце точок, які здійснюють коливання в од­наковій фазі.

Залежно від форми хвильової поверхні розрізняють хвилі ПЛОСКІ, СФЕРИЧНІ, ЦИЛІНДРИЧНІ та інші.

Форма хвильової поверхні визначається характеристиками джерела і властивостями середовища. На­приклад, точкове джерело в однорідному середовищі утворює сферичну хвилю.

ХВИЛЬОВИМ ФРОНТОМ називають «передову хвильову поверхню». Вона відокремлює простір, в якому частинки коливаються, від простору, де частинки ще не втягнуті в процес коливань. Хвильовий фронт переміщується в просторі з фазовою швидкістю .

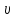ХВИЛЬОВИЙ ВЕКТОР у даній точці простору напрямлений по нормалі до хвильової поверхні і вказує напрям поширення хвилі в цій точці.

Модуль хвильового вектора дорівнює k = 2/ . Він назива­ється ХВИЛЬОВИМ ЧИСЛОМ. Хвильове число показує скільки довжин хвиль поміститься на довжині, що виражається числом 2π.

; → ,

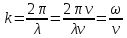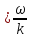де 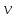-частота коливань, 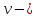фазова швидкість хвилі.

Фазова швидкість дорівнює відношенню циклічної частоти до хвильового числа.

РІВНЯННЯ ПЛОСКОЇ ХВИЛІ

Рівняння хвилі — це формула, яка дає змогу знайти зміщення s від положення рівноваги частинки, координати якої x, y, z, у момент часу t

s = s(x, у, z, t).

Уявімо собі джерело у вигляді нескінченної площини, перпендикулярної до осі х і розміщеної на початку координат, тобто при x = 0. Кожна точка площини здійснює гармонічні коливання, рівняння яких: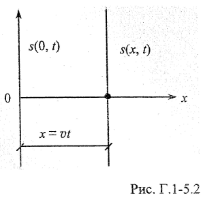

Очевидно, що хвильові поверхні теж будуть плоскі і тому хвиля буде одновимірною. Розглянемо коливання в точці, координата якої х. Частинка. яка міститься в цій точці, коливається з тією самою частотою со, як і частинки біля джерела, і з амплітудою s₀ , але із запізненням.

Час, який потрібен хвилі, щоб дійти до цієї точки,

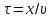
Тому рівняння коливань частинки буде таким:

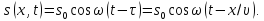
Ось так легко і просто ми отримали абсолютно правильне РІВНЯН­НЯ ПЛОСКОЇ ХВИЛІ. У цьому рівнянні: s — зміщення частинки від по­ложення рівноваги; 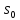— амплітуда коливань; х — координата; t — момент часу; 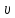— фазова швидкість.

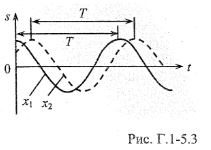
Узявши до уваги, що 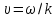, запишемо рівняння плоскої хвилі в ін­шому, більш поширеному вигляді:

Якщо хвиля поширюється у від’ємному напрямі осі х, то потрібно змінити знак перед координатою х, тобто

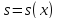У рівнянні хвилі дві змінні: х і s. Тому, коли з’являється необхідність графічно зобразити хвилю, будують залежність зміщення від часу при сталому x , або залежність зміщення від коор­динати при сталому часі (дивись рисунки).

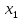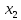У першому випадку ми дістанемо звичайний графік гар­монічних коливань для частинок із координатами і . Видно, що амп­літуди і періоди обох коливань однакові, а фази — різні.

У другому випадку ми отримаємо «миттєві знімки» біжучої хвилі для двох різних моментів часу 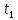і На останньому графіку показано, що відстань між частинками, які здійснюють коливання в од­ній фазі (довжина хвилі), залишається сталою.

У загальному випадку плоска хвиля може поширюватись не вздовж осі х, а в довільному напрямі. Тоді 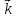буде вже вектором, а положення точки слід задавати, як звичайно, за допомогою радіуса-вектора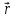. Рів­няння плоскої хвилі набере вигляду

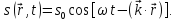
Можна розписати скалярний добуток хвильового вектора 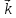на радіус-вектор :

,

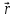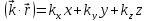і тоді рівняння набере вигляду

.

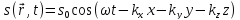Напрям поширення хвилі збігається з напрямом хвильового вектора, а він перпендикулярний до хвильової поверхні.

РІВНЯННЯ СФЕРИЧНОЇ ХВИЛІ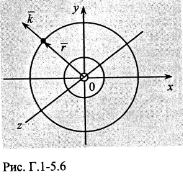

Сферична хвиля створюється точковим джерелом.

Хвильові поверхні — це сфери.

Хвильовий вектор у будь-якій точці перпендикулярний до хвильової поверхні, тобто збігається за напрямом з радіусом-вектором.

На відміну від плоскої хвилі амплітуда коливань частинок із мірою віддалення від джерела зменшується, тому через кожну наступну сферу протікає одна й та сама енергія, яка виділяється джерелом, але число час­тинок, які коливаються, зростає, як .

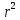Кожній частинці припадає менше енергії, і її амплітуда зменшується за законом 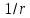. Рівняння сферичної хвилі:

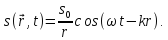
Зазначимо, що напрям фазової швидкості збігається з напрямом хвильового вектора k і з напрямом радіуса-вектора .

Зауважимо також, що наведені рівняння плоскої та сферичної хвиль придатні як для поздовжніх, так і для поперечних хвиль.

Диференціальне ХВИЛЬОВЕ РІВНЯННЯ

Рівняння хвилі ми одержали шляхом розмірковувань.

Насправді ж воно має бути розв’язком загального диференціального ХВИЛЬОВОГО РІВНЯННЯ, так само як рівняння гармонічних коливань

було розв’язком загального диференціального рівняння вільних незагасаючих коливань

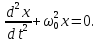
Спробуємо, як виняток, «відновити» диференціальне хвильове рівняння за відомим нам розв’язком цього рівняння.

У рівнянні плоскої хвилі

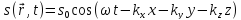
чотири змінні, а саме: х, у, z, t.

Візьмемо другі частинні похідні від зміщення за кожною з цих змінних

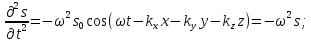
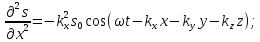
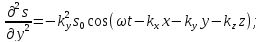
Додамо почленно останні три рівняння:

але

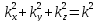, а

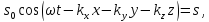
і тоді

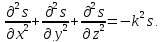
Виразимо s із першого рівняння

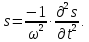
Дістаємо:

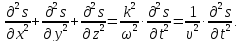
Математичний вираз 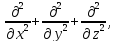який позначають грецькою літерою ∆ (дельта) або 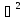(набла квадрат) називають оператором Лапласа.

Зліва маємо оператор Лапласа 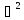від зміщення. Тому остаточно:

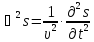
Отже, дістали ХВИЛЬОВЕ ДИФЕРЕНЦІАЛЬНЕ РІВНЯННЯ.

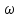У ньому немає ніяких конкретних характеристик частин­ки, яка коливається, немає ні амплітуди , ні частоти , ні фа­зи 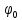Тому рівняння описує не якусь конкретну хвилю, а будь-яку хвилю.

Так само диференціальне рівняння гармонічних коливань опи­сувало цілий клас коливань.

У хвильовому рівнянні міститься лише одна стала — це фазова швидкість , яка не залежить від ха­рактеристик джерела, таких як частота або амплітуда, а повністю визначається властивостями середови­ща, в якому поширюється хвиля.

ФАЗОВА ШВИДКІСТЬ ХВИЛІ

Припустимо, що фаза хвилі з часом залишається сталою:

.

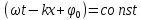Продиференціювавши це рівняння, вважаючи змінними х і t дістанемо швидкість поширення хвилі

→

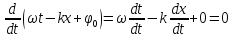
Швидкість 𝛖— це швидкість переміщення даного значення фази, і вона збігається зі швидкістю по­ширення хвилі. Тому цю швидкість називають фазовою швидкістю хвилі.

ГРУПОВА ШВИДКІСТЬ ХВИЛЬ

Раніше ми розглядали монохроматичну хвилю, яку легко уявити у вигляді косинусоїди, що біжить із фазовою швидкістю. З таким самим успіхом у пружному середовищі може поширюватися й одиночне збудження будь-якої форми, наприклад, у вигляді прямокутного імпульсу або серії імпульсів.

Відомо, що будь-яка періодична функція може бути розкладена в ряд Фур’є. Тому імпульс довільної форми, який поширюється, може бути замінений системою гармонічних хвиль різних частот.

У такому разі кажуть про ГРУПУ ХВИЛЬ, або ХВИЛЬОВИЙ ПАКЕТ.

ГРУПОВА ШВИДКІСТЬ 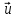- характеризує рух декількох монохроматичних хвиль (групи).

Швидкість поширення хвильового пакета, або групи хвиль, називається ГРУПОВОЮ ШВИДКІСТЮ.

На перший погляд не ясно, навіщо потрібно вводити поняття групової швидкості, адже ж ми раніше встановили, що фазова швидкість хвилі залежить тільки від властивостей середовища і вона має бути однаковою для хвиль будь-яких частот.

На жаль, досліди, які були проведені з хвилями високих частот, показали, що швидкість хвилі може залежати від її частоти або довжини.