
Л_2_4_3_Явище_електромагнітної_індукції
.docxЯвище електромагнітної індукції.
1. Явище електромагнітної індукції. Закон Фарадея. Правило Ленца
Явище електромагнітної індукції було відкрите англійським фізиком М.Фарадеєм у 1831 році і заключається у виникненні індукційного струму в замкнутому контурі при зміні магнітного потоку через площу, обмежену цим контуром. Величина е.р.с. дорівнює швидкості зміни магнітного потоку – це закон Фарадея
 (1)
(1)
Тут dФ – зміна магнітного потоку через контур, dt – час, за який відбулася зміна потоку на dФ.
Якщо витків в контурі не один а N то
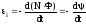 .
.
Добуток магнітного потоку Ф на кількість витків N називається потокозчепленням
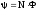 .
.
Знак (-) відображає правило Ленца про напрям індукційного струму. Індукційний струм завжди має такий напрям, при якому він своїм магнітним полем протидіє зміні магнітного потоку, який його викликав. Якщо потік зовнішнього поля зростає, поле індукційного струму протилежне йому, якщо ж потік зовнішнього поля зменшується, то магнітне поле індукційного струму співпадає з ним.
2. Виникнення електрорушійної сили в розімкнутому провіднику
при переміщенні в магнітному полі.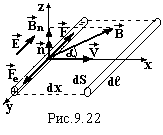
Електрорушійна сила виникає і в
розімкнутому провіднику, якщо він
рухається в магнітному полі. Під дією
сили Лоренца
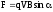 вільні електрони зміщуються до одного
кінця провідника. Відбувається. розділення
зарядів. Виникає електричне поле
напруженістю Е, яке діючи на заряд з
силою
вільні електрони зміщуються до одного
кінця провідника. Відбувається. розділення
зарядів. Виникає електричне поле
напруженістю Е, яке діючи на заряд з
силою
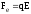 і перешкоджає подальшому
перерозподілу зарядів. В стаціонарному
випадку ці сили рівні між собою
і перешкоджає подальшому
перерозподілу зарядів. В стаціонарному
випадку ці сили рівні між собою
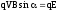 .
Напруженість
.
Напруженість
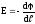 .
Одержуємо для е.р.с.
.
Одержуємо для е.р.с.
 (2)
(2)
Якщо врахувати, що
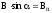 ,
,
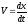 ,
,
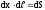 ,
,
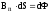 ,
одержимо формулу (1):
,
одержимо формулу (1):
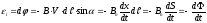 .
.
3. Явище самоіндукції. Індуктивність. Індуктивність довгого
соленоїда
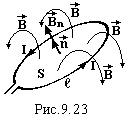
При протіканні струму по будь-якому контуру створюється магнітне поле, лінії індукції якого пронизують площу S цього ж самого контуру. Магнітний потік у цьому випадку називається потоком самоіндукції
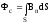 .
.
Проекцію вектора індукції на нормаль
до поверхні
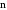 запишемо із закону Біо-Савара-Лапаласа
і принципу суперпозиції
запишемо із закону Біо-Савара-Лапаласа
і принципу суперпозиції
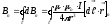 .
.
Тоді потік самоіндукції
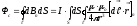
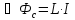 (3)
(3)
Тут
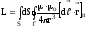 (4)
(4)
залежить тільки від геометричних розмірів контуру (S, ℓ) та магнітних властивостей середовища (μ) і називається індуктивністю контура. Індуктивність - це коефіцієнт пропорційності між потоком самоіндукції і струмом у власному контурі.
Одиницею вимірювання індуктивності є
генрі (Гн).
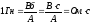 .
.
Якщо маємо не один виток, а N, то індуктивність буде в N разів більшою, тобто будемо мати справу з потокозчепленням самоіндукції
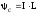 . (5)
. (5)
Зважаючи на складність розрахунку поверхневого і криволінійного інтегралів за формулою (4), індуктивність розраховують простіше із застосуванням закону повного струму.
Приклад. Розрахуємо індуктивність довгого соленоїда. Знайдемо потозчеплення самоіндукції, врахувавши
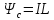 .
.
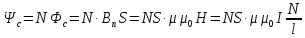 .
.
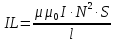 .
.
Звідки індуктивність довгого соленоїда:
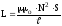 .
(6)
.
(6)
Формула (6) свідчить, що індуктивність довгого соленоїда залежить від геометричних розмірів котушок і магнітних властивостей осердя і не залежить від сили струму.
Враховуючи формулу (3) закон Фарадея може бути записаний таким чином:
 .
(7)
.
(7)
4. Зміна струму в котушці при його вмиканні і вимиканні. Фізичний зміст індуктивності
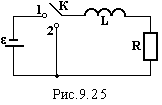
Знайдемо закон зміни струму при вмиканні котушки в коло джерела е.р.с. і при вимиканні .
При розімкнутому ключі К струм у
колі відсутній. Після замикання ключа
в положення 1 в котушці струм наростає.
Він спричиняє виникненя в цій же котушці
змінного магнітного поля і е.р.с.
самоіндукції. Закон Ома запишеться так
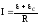 ,
а враховуючи рівняння (7), маємо
,
а враховуючи рівняння (7), маємо
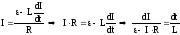 .
Інтегрування з початковими умовами:
при t = 0, I
= 0, дає
.
Інтегрування з початковими умовами:
при t = 0, I
= 0, дає
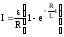 (8)
(8)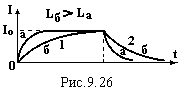
експоненціальне зростання струму
(дивись рисунок, криві 1). При
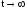 струм досягає стаціонарного значення
струм досягає стаціонарного значення
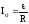 .
.
Після досягнення стаціонарного струму перемикання ключа в положення 2 утворює контур, в якому діє тільки е.р.с. самоіндукції.
Закон Ома має вид:
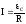 ,
,
або
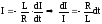 .
.
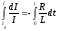 .
.
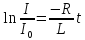 →
→
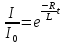 →
→
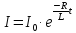
Враховуючи, що
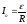 ,
отримаємо:
,
отримаємо:
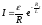 (9)
(9)
експоненціальний спад струму (див. рис., криві 2).
Відношення
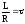 називається часом релаксації. Це час,
за який струм змінюється в е
разів (е = 2,718 - основа
натурального логарифму).
називається часом релаксації. Це час,
за який струм змінюється в е
разів (е = 2,718 - основа
натурального логарифму).
Вирази (8) і (9) показують, що із збільшенням індуктивності зменшується швидкість зміни струму у контурі (див. рис., а і б). Таким чином, індуктивність є міра інертності котушки до зміни в ній електричного струму.
5. Енергія та густина енергії магнітного поля
Для збільшення струму в котушці необхідно виконати роботу проти е.р.с. самоіндукції
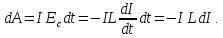
Ця робота перетворюється в енергію магнітного поля
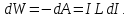
Інтегрування в межах від 0 до І дає
 . (10)
. (10)
Густина енергії w – це енергія, зосереджена в одиниці об’єму простору, де створене магнітне поле
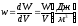 .
(11)
.
(11)
Знайдемо її на прикладі магнітного поля довгого соленоїда. Якщо нехтувати крайовими ефектами, то це поле зосереджене всередині котушки, а отже відомий об’єм V = S∙ℓ. Енергію знаходимо по (10) з врахуванням (6). Одержуємо
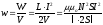 .
.
Враховуючи, що для довгого соленоїда
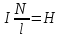 ,
,
маємо для густини енергії магнітного поля
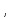 (12)
(12)
де H
– напруженість магнітного поля, B
- його індукція, μ -магнітна проникність
середовища,
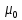 - магнітна стала.
- магнітна стала.
