Вільні незгасаючі коливання Вступ

Коливальними називаються процеси, які характеризуються певною повторюваністю і періодичним поверненням до початкового стану.

У природі існує безліч фізичних об’єктів, які здійснюють періодичні коливання. Ці об’єкти можуть істотно відрізнятися один від одного як за фізичною природою, так і за характером коливань. Але, як виявилось, загальні властивості не залежать від типу системи. Відповідно, математичні рівняння, що описують коливання в системах різної природи, виявляються формально однаковими. Відмінності мають частковий характер і стосуються лише фізичного тлумачення тих чи інших математичних величин, які входять до рівняння. Тому, вивчаючи загальні властивості в якійсь одній фізичній системі, ми автоматично дістаємо низку базових закономірностей, які є спільними для всіх без винятку систем.

Розрізняють коливання ВІЛЬНІ і ВИМУШЕНІ.

Вільні коливання виконує система, до якої не підводиться зовні енергія. Тобто, це коливання в системах, представлених самим собі.

Якщо при цьому система не витрачає своєї енергії, то її повна енергія залишається весь час сталою і коливання будуть незгасаючими.

Якщо ж енергія системи зменшується, наприклад через виконання роботи проти зовнішніх сил, то коливання будуть зaгасаючими.

Вимушені коливання виникають в системах, які зазнають періодичної зовнішньої дії. Це може бути сила, напруга і т. ін. Вимушені коливання, здебільшого незгасаючі.

Розглянемо паралельно механічні (на прикладі пружинного маятника) та електричні (на прикладі коливального контура) коливання.

В курсі фізики вивчають такі коливні системи: математичний, фізичний, пружинний, крутильний маятники, коливальний контур (електронний маятник).

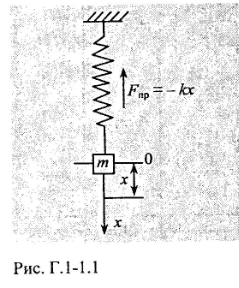
Вільні незгасаючі механічні коливання

Незгасаючі механічні коливання виконуватиме система, що складається з тіла масою m і пружини, яка повертає тіло до положення рівноваги. Таку систему називають ПРУЖИННИМ МАЯТНИКОМ.

Якщо вивести тіло з положення рівноваги, відхиливши його на відстань x, то воно набуде потенціальної енергії, що дорівнює роботі розтягнення пружини. Відпустивши тіло, ми даємо йому змогу повернутися в початкове положення рівноваги. У цьому положенні вся потенціальна енергія перейде в кінетичну, тіло за інерцією продовжуватиме рух, стискаючи пружину і виконуючи роботу стискання .

Коли всю кінетичну енергію буде витрачено на роботу стискання, тіло зупиниться, набувши потенціальної енергії. А це означає, що процес перетворення кінетичної енергії в потенціальну, і навпаки, буде відбуватися як завгодно довго, тобто тіло виконуватиме незгасаючі коливання від -x до +x.

Знайдемо рівняння руху тіла m.

За другим законом динаміки швидкість зміни імпульсу дорівнює сумі всіх сил, які діють на тіло:

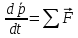_і

Надалі знаки векторів можна не записувати, оскільки рух одномірний. Тіло вважатимемо матеріальною точкою з масою m. У нашому випадку діє єдина сила – пружна повертаюча сила F_пр.. Згідно із законом Гука при малих зміщеннях сила пружності прямо пропорційна до зміщення:

F_пр = - kx,

де k - КОЕФІЦІЕНТОМ ЖОРСТКОСТІ пружного елемента.

Знак «мінус» означає, що сила напрямлена в бік, протилежний зміщенню. Маса m стала, і тому

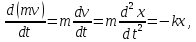
або

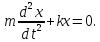
Поділивши обидві частини рівняння на масу m і ввівши заміну ,

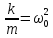дістанемо ДИФЕРЕНЦІАЛЬНЕ РІВНЯННЯ НЕЗГАСАЮЧИХ МЕХАІЧНИХ КОЛИВАНЬ

.

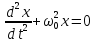Загальний розв’язок цього лінійного диференціального рівняння другого порядку відомий:

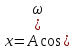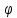₀ t +₀).

Це також рівняння руху, але вже в явному вигляді. Такі коливання системи називають гармонічними. Тобто: гармонічнними коливаннями називають коливання, при яких параметри системи змінюються за законом sin або cos.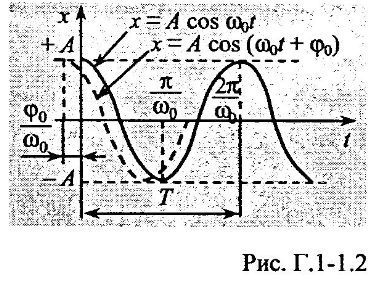

Значення косинуса змінюються в межах від +1 до -1. Значення зміщення від положення рівноваги лежать у межах від +А до –А . Тому А - найбільше зміщення від положення рівноваги, називається АМПЛІТУДОЮ КОЛИВАНЬ.

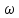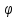Величина ₀t +₀ 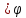, яка є аргументом косинуса, називається ФАЗОЮ КОЛИВАНЬ. У початковий момент часу при t = 0 значення фази 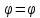₀ . 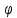₀ - називається ПОЧАТКОВОЮ ФАЗОЮ.

На рисунку зображено залежність зміщення x від часу t. Якщо початкова фаза дорівнює 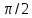, то замість косинуса буде синус - теж гармонічна функція. Оскільки косинус - функція періодична, то зміщення повторюватиметься через інтервал часу, що дорівнює періоду коливань. ПЕРІОДОМ КОЛИВАНЬ називають час одного повного коливання.

Кількість коливань за одиницю часу v називають ЧАСТОТОЮ КОЛИВАНЬ.

v =1/T.

Оскільки період косинуса дорівнює 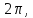то 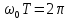, звідки

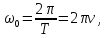
де 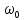- ЦИКЛІЧНА, або КОЛОВА, ЧАСТОТА КОЛИВАНЬ.

Циклічна частота визначається властивостями самої коливальної системи. Під час виведення диференціального рівняння руху ми вводили позначення

.

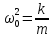Можна сказати, що колова частота визначається відношенням сил пружності до сил інерції. Її називають ВЛАСНОЮ ЧАСТОТОЮ і тому ставлять індекс нуль.

Тоді період коливань пружинного маятника визначається з формули:

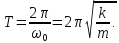
Якщо ми знаємо рівняння руху, то легко обчислити будь-які кінематичні характеристики коливань.

ШВИДКІСТЬ ГАРМОНІЧНИХ КОЛИВАНЬ дістанемо, узявши першу похідну від зміщення за часом:

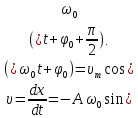
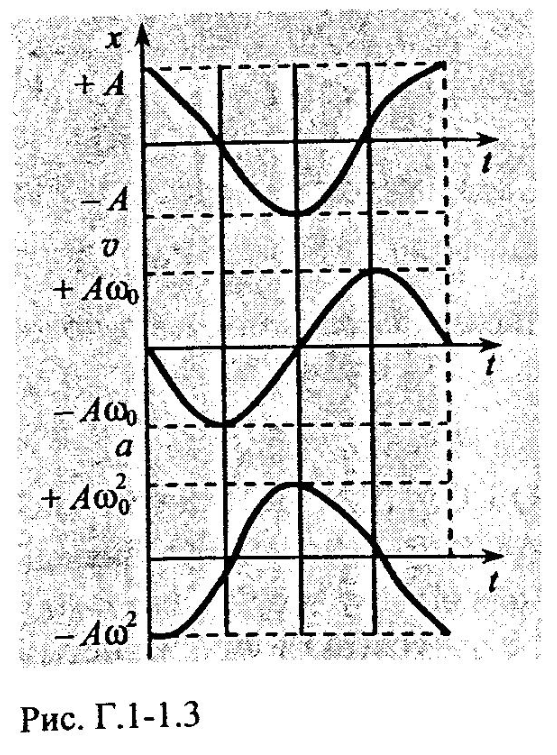
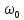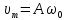Швидкість також виконує гармонічні коливання з тією самою частотою , що й зміщення, та з амплітудою , яка залежить не тільки від амплітуди зміщення, а й від колової частоти і відрізняється за фазою від зміщення на .

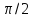ПРИСКОРЕННЯ ГАРМОНІЧНИХ КОЛИВАНЬ це перша похідна від швидкості за часом, або друга похідна від зміщення за часом

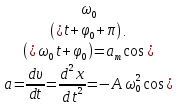
Прискорення також виконує гармонічні коливання з частотою 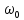та амплітудою 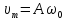, яка залежить не тільки від амплітуди зміщення, а й зміщення на .

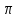Прискорення і зміщення перебувають, як кажуть у ПРОТИВАЗІ. Це означає, що коли зміщення досягає максимального значення, що дорівнює амплітуді, прискорення також сягає свого максимального, але від'ємного значення. На рисунку вище зображено графіки залежності зміщення, швидкості і прискорення від часу. Початкову фазу зміщення взято такою, що дорівнює нулю.

Обчислимо тепер енергію коливань.

КІНЕТИЧНА ЕНЕРГІЯ

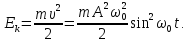
ПОТЕНЦІАЛЬНА ЕНЕРГІЯ дорівнює роботі проти пружної повертальної сили:

.

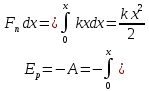Враховуючи, що k =

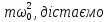
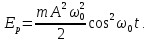
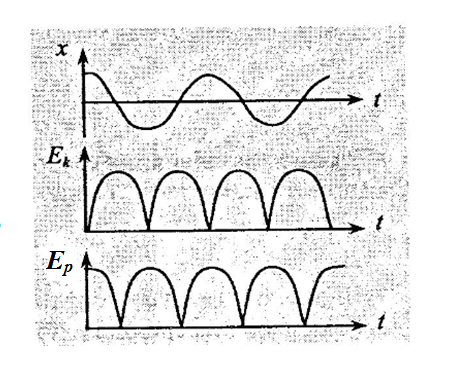
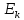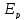На рисунку зіставлено графіки залежностей і від часу. Бачимо, що період зміни кінетичної і потенціальної енергії удвічі менший за період зміщення.

У процесі коливань відбувається перетворення кінетичної енергії на потенціальну, та навпаки. Коли зміщення дорівнює нулю, то потенціальна енергія дорівнює нулю, а кінетична досягає свого максимального значення:

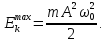
Коли зміщення досягає свого максимального значення, кінетична енергія дорівнює нулю, а потенціальна досягає свого максимального значення:

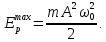
ПОВНА МЕХАНІЧНА ЕНЕРГІЯ дорівнює сумі кінетичної і потенціальної енергії:

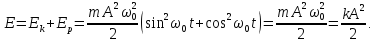
Як бачимо, повна механічна енергія незгасаючих механічних коливань стала і дорівнює максимальному значенню кінетичної енергії, або максимальному значенню потенціальної енергії.