2.8. Корреляционный анализ
Пример 1. Зависимость потребления обуви от возраста потребителей представлена в таблице 52. Необходимо выяснить, существует зависимость между потреблением обуви на одного человека в год и возрастом потребителей.
Таблица 52
Исходные данные для расчета
Возраст потребителя, лет |
Потребление обуви, пар на одного человека в год |
До 8 |
5,0 |
8 – 16 |
4,5 |
17 – 19 |
5,0 |
20 – 30 |
4,5 |
31 – 40 |
4,0 |
41 – 50 |
3,0 |
старше 50 |
2,0 |
Всего |
28,0 |
Расчеты представим в таблице 53. Анализ зависимости потребления обуви от возраста потребителей показывает, что с увеличением возраста потребление уменьшается. Среднее потребление на одного человека составляет четыре пары в год. Если средний возраст потребителей будет увеличиваться (что, кстати, сегодня характерно для России), то следует ожидать уменьшения среднего потребления на одного человека, т. е. спрос на обувь может уменьшиться.
Таблица 53
Расчетная таблица
Возраст потребителя, лет (х) |
Потребление обуви, пар на одного человека в год (у) |
Середина возрастного интервала |
хy |
x2 |
y2 |
До 8 |
5,0 |
4 |
20,0 |
16 |
25 |
8 – 16 |
4,5 |
12 |
54,0 |
144 |
20,25 |
17 – 19 |
5,0 |
18 |
90,0 |
324 |
25 |
20 – 30 |
4,5 |
25 |
112,5 |
625 |
20,25 |
31 – 40 |
4,0 |
35 |
140,0 |
1225 |
16 |
41 – 50 |
3,0 |
45 |
135,0 |
2025 |
9 |
старше 50 |
2,0 |
55 |
110,0 |
3025 |
4 |
Всего |
28,0 |
194 |
661,0 |
7384 |
119,5 |
Управленческие решения, основывающиеся на такой информации, связаны с определенным риском, так как анализируемые величины носят вероятностный характер. Для определения степени этого риска рассчитаем коэффициент корреляции:
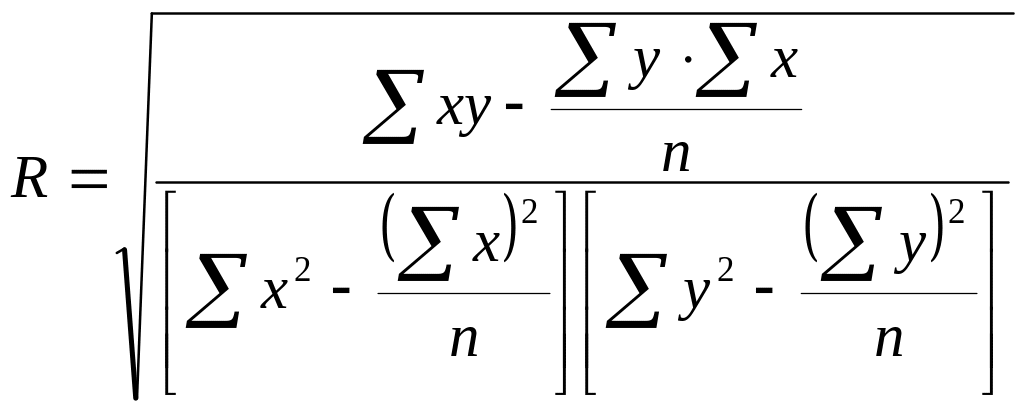
Величина коэффициента корреляции (- 0,93) говорит о том, что между потреблением обуви и возрастом потребителей существует обратная корреляционная зависимость, теснота которой достаточно высока. Следовательно, риск решений, принимаемых на основе анализа этой зависимости, невелик.
Пример 2. Оздоровительный центр «Аэлита», рекламируя свои услуги, предлагает клиентам за короткий срок снижение веса более 10 кг. По результатам выборочного обследования 15 женщин, воспользовавшихся услугами центра, были получены следующие данные о снижении их веса (табл. 54).
Таблица 54
Данные о снижении веса пациентов оздоровительного центра
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
Снижение веса, кг |
10,2 |
7,6 |
6,1 |
8,4 |
6,0 |
5,7 |
13,7 |
6,9 |
5,2 |
6,1 |
5,0 |
3,7 |
4,7 |
3,6 |
3,2 |
Оценить вероятность снижения веса пациентов оздоровительного центра на 10 кг. На основании этого сделать вывод, необходимо ли изменить информацию в рекламном сообщении?
Решение. Выборочная дисперсия равна:
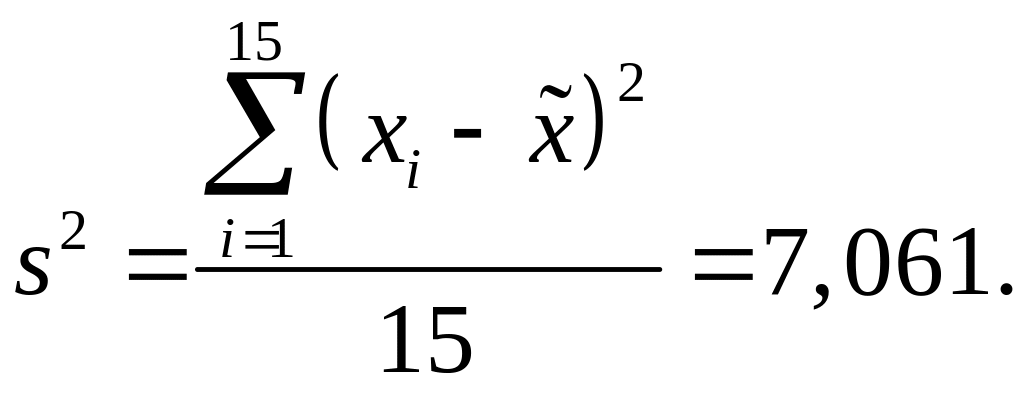
Следовательно, средняя квадратическая ошибка выборки составит:
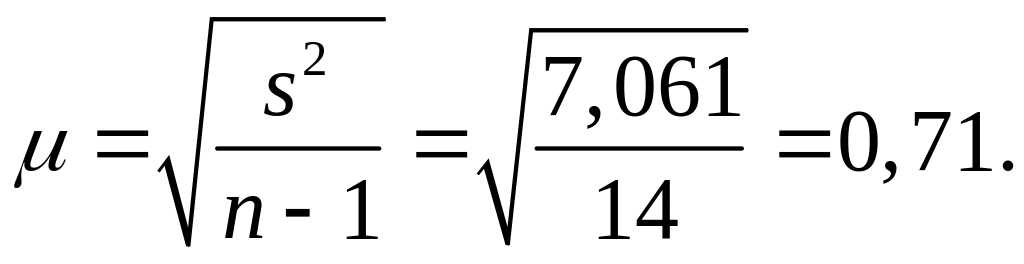
Оценим с вероятностью 0,99 предел возможных расхождений выборочной средней и генеральной средней. Так как число степеней свободы равно 14 (k = n–1=15-1), то по таблице распределения Стьюдента находим, что значение t, соответствующее вероятности 0,99, равно 2,977.
Тогда с вероятностью 0,99 можно предполагать, что ошибка выборочной средней будет не больше 2,977·0,71=2,114 кг, а снижение веса пациентов оздоровительного центра будет находиться в пределах от 4,3 до 8,52 кг (6,41±2,11).
Следовательно, указанное в рекламе снижение веса на 10 кг имеет столь малую вероятность, что считается событием практически невозможным. Необходимо изменение информации в рекламе.
Задания по теме:
Задача 1. Экспертным методом установите тесноту связи между средним баллом абитуриента по ЕГ и выбором специальности маркетолога в вашем институте.
Задача 2. На основании экспертных данных установите тесноту связи между средним баллом выписки диплома и уровнем достижимой карьеры.
Задача 3. Экспертным методом установите связь между уровнем зарплаты маркетолога и имиджем предприятия.