2.3. Метод «парных сравнений» в ранжировании альтернатив

Ранжирование (choice-ordering) — к этой группе относятся методики, которые имеют более структурированные стимулы. Методика имеет множество модификаций. Например, респондентам раздают списки характеристик исследуемого продукта или рекламы и просят выбрать те характеристики, которые наиболее ему\ей соответствуют или просят проранжировать характеристики по какому-либо признаку (например, по степени важности).

Примеры по теме:

Пример 1. Для выработки стратегий управления маркетингом в ситуационном анализе требуются данные о конкурентоспособности рыночных товаров или их фирм-производителей. Формализация оценки однотипных товаров на конкурентоспособность затруднительна и может быть необъективна из-за множества сравниваемых атрибутов. В этом случае целесообразно использовать аппарат метода экспертных оценок.

Рассмотрим пример ранжирования, где в качестве объекта выступает группа товаров-конкурентов. Ранжирование предполагает установление логической или численной закономерности в доминировании (предпочтении) сравниваемых объектов. Для решения поставленной задачи рассмотрим метод «парных сравнений» по какому-либо критерию. Исходя из принципов модели парных сравнений принимается: если среди сравниваемых объектов (товаров) Аi, Аj наблюдается отношение Аi>Aj по критерию k, тo в перекрестии сравниваемых объектов экспертной таблицы 6 заносим число 1,5; если наблюдается равенство Аi=Aj тo в таблицу заносим 1,0; если Ai,<Aj, заносим 0,5, где Аij – факторы внешней среды. Составим таблицу 6 конкурирующих товаров, влияющих на принятие оптимальной маркетинговой стратегии управления.

Таблица 6

Экспертные данные по сравниваемой товарной группе

Товары-конкуренты	Товар А1	Товар А2	Товар А3	Товар А4		Сумма баллов по строкам (∑i)		Вес фактора (ai)
А1	1	1,5	0,5	1,5		4,5		0,29
А2	0,5	1	0,5	1,0		3,0		0,19
А3	1,5	1,5	1	0,5		4,5		0,29
А4	0,5	1,0	1,5	1,0		4,0		0,25
ИТОГО:					16,0		1,0

На основании значимости веса факторов а_ij таблицы 6 (а₁=а₃>а₄>а₂) приоритетность (ранжируемость) рассматриваемых факторов примет вид: А1=А3>A4>A2.

Рассмотрим процесс увеличения точности нормированных значений ai. Для этого весовая характеристика товара умножается на ее ранговое значение (столбец на ∑), и полученные произведения будут элементами новой матрицы парных сравнений, т.е. a_ij∙∑a_i = a_ij⁽¹⁾. Новая матрица примет вид табл. 7.

Таблица 7

Матрица первого преобразования

Товары-конкуренты	Товар А1	Товар А2	Товар А3	Товар А4	Сумма баллов по строкам (∑)	Вес фактора (ai)
А1	1,0∙4,5=4,5	1,5∙3,0=4,5	0,5∙4,5=2,25	1,5∙4,0=6,0	17,25	0,28
А2	0,5∙4,5=2,25	1,0∙3,0=3,0	0,5∙4,5=2,25	1,0∙4,0=4,0	11,5	0,19
А3	1,5∙4,5=6,75	1,5∙3,0=4,5	1,0∙4,5=4,5	0,5∙4,0=2,0	17,75	0,29
А4	0,5∙4,5=2,25	1,0∙3,0=3,0	1,5∙4,5=6,75	1,0∙4,0=4,0	16,0	0,26
ИТОГО:					62,5	1,0

Из уточненного расчета по весу факторов (ai) ранжированный ряд принял значение А3> А1>A4>A2.

Наибольшее отклонение от предыдущего значения коэффициента приоритетности составляет фактор А4, тогда коэффициент приоритетности

∆ = (0,26-0,25)/0,25х100% = 4%.

Для ординарных маркетинговых управленческих решений допустимым условием погрешности расчетов является величина ∆max < (2,0 ÷ 3,0)%. В нашем примере коэффициент приоритетности превышает величину погрешности ∆>∆max, следовательно, необходимо операцию с парными сравнениями повторить по ранее рассмотренной методике с данными в табл. 8.

Таблица 8

Оптимизированная таблица

Товары-конкуренты	Товар А1	Товар А2	Товар А3	Товар А4	Сумма баллов по строкам (∑)	Вес фактора (ai)
А1	1,0∙17,25=17,25	1,5∙11,5=17,25	0,5х17,75=8,88	1,5∙16=24	67,38	0,28
А2	0,5∙17,25=8,63	1,0∙11,5=11,5	0,5∙17,75=8,88	1,0∙16=16	45,01	0,19
А3	1,5∙17,25=25,88	1,5∙11,5=17,25	1,0∙17,75=17,75	0,5∙16=8	68,88	0,29
А4	0,5∙17,25=8,63	1,0∙11,5=11,5	1,5∙17,75=26,63	1,0∙16=16	62,76	0,26
ИТОГО:					244,03	1,0

Ранжируемый порядок товаров в таблице 8 не изменился: А3> А1>A4>A2.

Коэффициент приоритетности ∆ = (0,26-0,26)/0,26х100% = 0% свидетельствует о правильном процессе проведения ранжирования товаров и их числовых значений.

Пример 2. Методом ранжирования проведем независимую оценку Мi, i=1,…,n посредников (поставщиков, дилеров, дистрибьютеров и т.д.) в товарном бизнесе предприятия. Из практики работы известно, что посредники по своим бизнес-характеристикам довольно близки друг к другу. На основе экспертной матрицы ||Z|| построенной в табл. 9 проведем численную оценку посредников по критерию k, например, точности выполнения срока поставки. В этом случае, при незначительном различии сравниваемых посредников элемент матрицы примет вид:

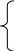0,8 , если посредник Рi хуже посредника Рj;

Zij = 1,0 , если посредник Рi равносилен Рj;

1,2 , если посредник Рi лучше Рj.

Посредники i, j входят во множество М=1,2,…n.

Рассмотрим конкретный пример. Эксперт на основании умозаключений заполняет матрицу анализа- ||Z|| для четырех дилеров Рi, i=1,2,3,4.

Таблица 9

Матрица экспертного анализа- ||Z|| четырех дилеров

i/j	Р1	Р2	Р3	Р4		Si	Qi
Р1	1,0	1,2	1,0	1,0	4,2	16,76	0,263
Р2	0,8	1,0	0,8	1,2	3,8	15,0	0,235
Р3	1,0	1,2	1,0	1,2	4.4	17,48	0,275
Р4	1,0	0,8	0,8	1,0	3,6	14,36	0,226
∑						63,6	1,0

Показатель важности Si или приоритетность посредника определяется по формуле Si= Zi1*∑Z1n +Zi2*∑Z2n +Zi3*∑Z3n + Zi4*∑Z4n+… , т.е.

S1=1,0*4,2 +1,2*3,8 +1,0*4,4 +1,0*3,6=16,76,

S2=0,8*4,2 +1,0*3,8 +0,8*4,4 +1,2*3,6=15,0,

S3=1,0*4,2 +1,2*3,8 +1,0*4,4 +1,2*3,6=17,48,

S4=1,0*4,2 +0,8*3,8 +0,8*4,4 +1,0*3,6=14,36.

Относительный вес сравниваемого посредника – Qi определится из формулы Qi = Si / ∑Si. На основании значений показателя Qi проводится ранжирование посредников P3>P1>P1>P4. Лучшим выглядит дилер под номером 3, он лучше номера 1 в С₃₁=0,275/0,263=1,045 раза и лучше аутсайдера 4 в С₃₄=0,275/0,226=1,21 раза.

Если в строке наблюдается равенство хотя бы в двух строках, целесообразно осуществить перемножение матрицы самой на себя и далее на результирующей матрице провести аналогичные операции ранжирования.

Еcли критериев анализа несколько (К=1,2,…,m) и каждый критерий имеет свой ранг или важность - q, то обобщенным критерием - Sо может выступать выражение Sо_i = ∑Qi*q_i / m. По значениям Sо_i (К i) строится ранжируемый ряд сравниваемых объектов. Если рейтинг определяют несколько экспертов, то итоговый вектор значений Р необходимо усреднить по правилам обработки экспертных оценок.

Следующий метод более объективно учитывает выбор поставщика, если путем ранжирования установлены значения оцениваемых критериев. Осуществим расчет рейтинга поставщиков товаров по данным, представленным в таблице 10.

Таблица 10

Данные по поставщикам

Критерий выбора	Удельный вес критерия		Оценка значения критерия у данного поставщика (по десятичной шкале)
	Поставщик 1	Поставщик 2
1. Надежность поставки	0,30	0,40	7
2. Цена	0,25	0,15	6
3. Качество товара	0,15	0,20	8
4. Условия платежа	0,15	0,15	4
5. Возможность внеплановых поставок	0,1	0,05	7
6. Финансовое состояние поставщика	0,05	0,05	4
ИТОГО	1,0	1,0	—

Выбор поставщиков включает сбор информации и создание банка данных о поставщиках, поиск оптимального поставщика, оценку результатов работы с выбранными поставщиками. Информация о поставщиках позволяет формировать банк данных, который необходимо проанализировать на основании специальных критериев, позволяющих осуществить отбор приемлемых поставщиков. Количество специальных критериев может варьироваться от одного до нескольких десятков. Все зависит от самого предприятия, которое определяет эти критерии. Как правило, используются критерии по цене, качеству, условиям поставки и их надежности.

Р ейтинг поставщика можно рассчитать по формуле:

где R_i — рейтинг i-го поставщика, ед.; q_уд.i — удельный вес критерия i-го поставщика, доля единицы; q₀ — оценка значения критерия предприятием, ед.; n — количество критериев выбора поставщика.

Используя данную формулу, рассчитаем рейтинг поставщиков:

R₁ = (0,3∙ 7) + (0,25∙ 6) + (0,15 ∙ 8) + (0,15 ∙ 4) + (0,1∙ 7) + (0,05 ∙ 4) = 6,3;

R₂ = (0,4 ∙ 7) + (0,15 ∙ 6) + (0,2 ∙ 8) + (0, 15 ∙ 4) + (0,05 ∙ 7) + (0,05 ∙ 4) = 6,45.

Так как рейтинг второго поставщика выше (R₂>R₁), предприятию по принятой системе показателей целесообразно развивать с ним взаимовыгодные отношения по закупке товаров.

Пример 3. Оценка рыночного рейтинга фирмы. Для оценки своей деятельности, фирма должна проводить независимую оценку своего положения на рынке. Путем сравнения фирмы с конкурентами необходимо создать ранжированный ряд вперед ушедших фирм и следующих за вами. Численное соотношение множества сравниваемых фирм по шкале какого-нибудь критерия представляет собой рейтинг, этого множества на шкале ранжирования.

Сущность метода. Эксперт, по критерию значимости – k, заполняет матрицу ||Z|| сравниваемых фирм с установкой числовых значений по следующим правилам:

а) при сильном различии сравниваемых фирм:

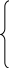0, если фирма i хуже фирмы j;

Zij^(k) = 1, если фирма i равносильна j;

2, если фирма i лучше фирмы j,

где i-номер строки матрицы, j- номер столбца матрицы,

б ) при среднем различии ранжируемых фирм:

0,5 , если фирма i хуже фирмы j;

Zij^(k) = 1,0 , если фирма i равносильна j;

1,5 , если фирма i лучше фирмы j,

в) при незначительном различии сравниваемых фирм:

0,8 , если фирма i хуже фирмы j;

Zij^(k) = 1,0 , если фирма i равносильна j;

1,2 , если фирма i лучше фирмы j,

Фирмы i, j входят во множество М=1,2,…n ранжируемых фирм. Сравниваемые пары образуют матрицу ||Z||_nxn значений этих соотношений, где n – число сравниваемых рекламных фирм.

Например, проведем сравнение четырех фирм (М=1,2,3,4) по критерию – k. Эксперт, путем попарного сравнения конкретных фирм заполняет матрицу:

М	1 2 3 4
1	1 0 1 0	2	0,125
Z = 2	2 1 0 2	5	0,312
3	1 2 1 2	6	0,376
4	2 0 0 1	3	0,185
		16	1

По составленной матрице ||Z||, в качестве первого этапа, производится «грубое» ранжирование путем построчного суммирования чисел , j= 1, 2, …n по каждой строке матрицы. Далее производится суммирование чисел матрицы и определение веса сравниваемой фирмы в виде коэффициента

П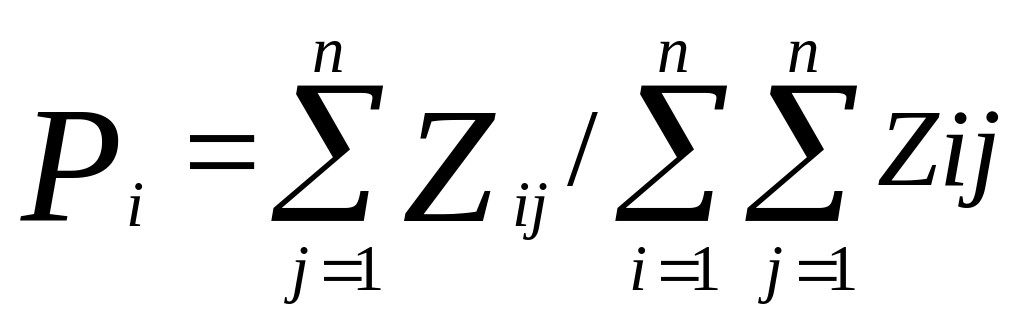 о значениям каждой строки образуется вектор , который представляет собой численное соотношение (рейтинги) сравниваемых фирм по критерию – k . На основании вектора Р строится рейтинговая шкала значимости рекламных фирм. Если веса объектов соотносятся как , то ряд предпочтений сравниваемых фирм выглядит I>m>…>n и их рейтинги соответственно r(i)>r(m)>…>r(n) на шкале рейтинга R^(k).

В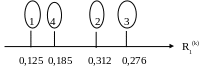 нашем примере рейтинговая шкала «грубого» ранжирования фирм выглядит следующим образом (рис. 1):

Рис. 1. Рейтинговая шкала первого этапа ранжирования

Анализ рейтинговой оси R₁^(k) позволит определить коэффициенты С_ij относительной силы сравниваемых фирм, т.е. C_ij=P_i/P_j которые показывают, во сколько раз рейтинг фирмы i весомее рейтинга фирмы j на шкале R по выбранному критерию - k или на сколько пунктов фирма i опережает или отстает от фирмы j .

Исходя из данных столбца С_ij матрицы Z^(k), рейтинговый порядок исследуемых фирм выглядит следующим образом: 3 > 2 > 4 > 1 , с коэффициентами: фирма 3 лучше 2 в С32 = 0, 376/0,312 = 1,205 или на 20,5%, фирма 2 лучше 4 в С24 = 0,312/0,185 = 1,686 или на 68,6%, фирма 4 лучше 1 в С41 = 0,185/0,125=1,48 или на 48%. Лидер 3 лучше аутсайдера 1 в С31 = 0,376/0,125 = 3,008.

Если рейтинг определяют несколько экспертов, то итоговый вектор значений Р необходимо усреднить по правилам обработки экспертных оценок.

На втором этапе “тонкого” ранжирования осуществляется перемножение матрицы ||Z|| саму на себя с получением новой матрицы Z₁= ||Z||x||Z||. С матрицы ||Z||₁ проводится аналогичная работа по суммированию строк и построение нового ряда значений векторов Р и R₂^(k). При «тонком» ранжировании весовые коэффициенты принимают более четкие значения и более утвердительно выглядит рейтинг фирм.

М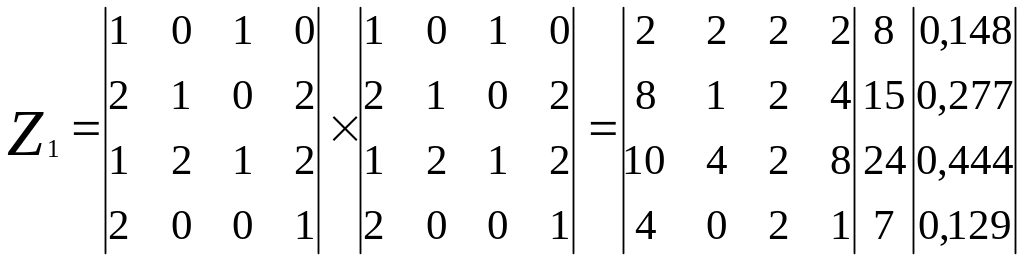 атрица «тонкого ранжирования для нашего примера выглядит:

Уточненный рейтинг сравниваемых фирм стал выглядеть на рейтинговой шкале R₂^(k) следующим образом (рис. 2):

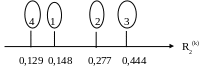
Рис. 2. Уточненная рейтинговая шкала

Из сравнения шкал R₁ и R₂ видно, лидерство сохранилось, аутсайдеры, находясь близко друг от друга, поменялись местами.

М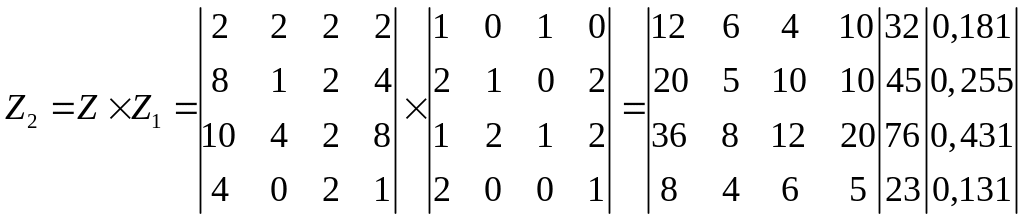 атрица второго уровня «тонкого» ранжирования примет вид:

По ее итоговому столбцу рейтинговая шкала второго уровня выглядит следующим образом (рис. 3):

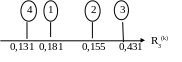
Рис. 3. Рейтинговая шкала 3 уровня

Таким образом, порядок рейтинга фирм стабилизируется и утверждаются весовые коэффициенты – С. Чем больше производить умножение полученных матриц на исходную ||Z||, тем точнее значения весов Р и весовых коэффициентов – С. Практически перемножение матриц можно закончить на 4 этапе.

Пример 4. Предприятие экспертным методом проводит исследование пяти своих товаров по 10-ти параметрам с целью выявить лучший и построить их ранжированный ряд. Исследование проводится по 10-ти бальной шкале. Данные опроса экспертов занесены в табл. 11.

Таблица 11

Данные опроса экспертов

№	Критерии оценки - К	Товары
		1	2	3	4	5
1	Цена	3,4	4,5	5,5	6,1	7,3
2	Качество	4,2	5,2	3,3	3,6	5,4
3	Дизайн	2,6	3,2	5,4	3,7	4,1
4	Цвет	1,5	3,1	4,3	5,6	5,2
5	Вес	2,5	3,8	5,7	3,7	7,1
6	Ручка	1,7	4,8	2,6	3,9	4,1
7	Упаковка	3,2	4,1	2,6	3,6	4,1
8	Функциональные возможности	5	1,7	7,5	4,8	3,9
9	Полезность	3	4,3	5,5	2,6	6,9
10	Материал	1	3,5	5,3	7,2	5,3
	Общая сумма балов	28,1	38,2	47,7	44,8	53,4

Решение:

1. Проставляем приоритеты по показателям принятым на фирме

К1 К4 К9 К2 К6 К3 К5 К10 К8 К7

Найдем цену критериев С_i и вес V_i критерия качества по следующим формулам: , где i - индекс строки, j- индекс столбца; .

Построим двузначную матрицу отношений критериев в виде табл. 12, где запись поля Кij=1 означает ситуацию Ki>Kj, запись Kij=0 означает Ki<Kj. Если в системе приоритетов наблюдалось равенство среди некоторых критериев, то матрица отношений должна принять трехзначную систему оценки (0, 1, 2), т.е. предпочтение, безразличие, доминирование.

Таблица 12

Матрица отношений оценочных критериев

ЧКК	К1	К2	К3	К4	К5	К6	К7	К8	К9	К10	Сi	Vi
К1		1	1	1	1	1	1	1	1	1	9	0,2
К2	0		1	0	1	1	1	1	0	1	6	0,13
К3	0	0		0	1	0	1	1	0	1	4	0,09
К4	0	1	1		1	1	1	1	1	1	8	0,18
К5	0	0	0	0		0	1	1	0	1	3	0,07
К6	0	0	1	0	1		1	1	0	1	5	0,11
К7	0	0	0	0	0	0		0	0	0	0	0
К8	0	0	0	0	0	0	1		0	0	1	0,02
К9	0	1	1	0	1	1	1	1		1	7	0,16
К10	0	0	0	0	0	0	1	1	0		2	0,04
Итого											45	1

Из матрицы получаем общую цену критериев и общий вес критериев .

2. Рассмотрим наши показатели и приблизим их к эталону, составив табл. 13.

Таблица 13

№	Критерии - К	Товары и их оценки aij					Эталонное значение aiэ	Направление экстремумов
		1	2	3	4	5
1	Цена	3,4	4,5	5,5	6,1	7,3	3,4	min
2	Качество	4,2	5,2	3,3	3,6	5,4	5,4	max
3	Дизайн	2,6	3,2	5,4	3,7	4,1	5,4	max
4	Цвет	1,5	3,1	4,3	5,6	5,2	5,6	max
5	Вес	2,5	3,8	5,7	3,7	7,1	2,5	min
6	Ручка	1,7	4,8	2,6	3,9	4,1	1,7	min
7	Щетина	3,2	4,1	2,6	3,6	4,1	4,1	max
8	Функциональные возможности	5	1,7	7,5	4,8	3,9	7,5	max
9	Полезность	3	4,3	5,5	2,6	6,9	6,9	max
10	Материал	1	3,5	5,3	7,2	5,3	1	min

3. Найдем относительный показатель качества каждого товара при условии:

а) , если критерий стремиться к максимуму (p_ij → max), где а_ij – численное значение оценки i-го товара;

б) , если критерий ценен при его минимизации (p_ij →min).

После преобразования таблица 3.8 будет выглядеть в виде табл. 14.

Таблица 14

Приведенные показатели качества сравниваемых товаров

№	Критерии	Товары и показатели качества pij					Эталон	Направление экстремумов
		1	2	3	4	5
1	Цена	1	0,76	0,62	0,56	0,47	1	min
2	Качество	0,78	0,96	0,61	0,67	1	1	max
3	Дизайн	0,48	0.59	1	0,69	0,76	1	max
4	Цвет	0,27	0,55	0,77	1	0,93	1	max
5	Вес	1	0,66	0,44	0,68	0.35	1	min
6	Ручка	1	0,35	0,65	0,44	0,41	1	min
7	Упаковка	0,78	1	0,63	0,88	1	1	max
8	Функциональные возможности	0,67	0,23	1	0,64	0,52	1	max
9	Полезность	0,43	0,62	0,79	0,38	1	1	max
10	Материал	1	0,29	0,19	0,14	0,19	1	min

4.Найдем оценку качества по каждому товару, используя интегральный критерий:

, при условии .

Результаты вычислений представлены в табл. 15.

Таблица 15

Итоговые значения экспертного анализа

Товар	1	2	3	4	5
Интегральный критерий качества товара	2,2854	3,4383	3,0232	3,5224	3,0833

По данным таблицы 3.10 построим ранжированный ряд качества исследуемых товаров: 3,5225 >3,4383 >3,0833 > 3,0232> 2,2854, что соответствует Q > Q > Q > Q >Q . Данный ряд при условии свидетельствует, что товар под номером 1 более приближен к эталону.

Задачи по теме:

Задача 1. Проранжировать вузы-конкуренты вашего города по критерию имиджа.

Задача 2. Проранжируйте ваши мотивационные факторы (5-6 видов), оказывающие влияние на выбор специальности.

Задача 3. Проранжируйте важнейшие факторы, определяющие имидж менеджера-маркетолога.