9.3. Производство.

В рамки модели общего равновесия нам необходимо включить также производство. При наличии производства количества товаров, определяющие начальный запас, не являются постоянными. Их можно произвести больше или меньше в зависимости от уровня рыночных цен.

Первая и вторая теоремы экономики благосостояния. Для экономики, в которой имеет место не только обмен, но и производство, также справедливо утверждение первой теоремы экономики благосостояния. В такой экономике конкурентное равновесие будет эффективным по Парето при условии, что фирмы, максимизирующие прибыль, являются конкурентными. При этом максимизация прибыли конкурентными фирмами гарантирует лишь эффективность, но не справедливость распределения богатства.

Выше мы установили, что в экономике одного только (чистого) обмена при выпуклых предпочтениях любое распределение, эффективное по Парето, может быть конкурентным равновесием. Этот результат имеет силу и для экономики, включающей в себя фазы обмена и производства. Однако теперь выпуклыми должны быть не только предпочтения потребителей, но и производственные множества фирм. Производственные множества определяются применяемыми фирмами технологиями. Выпуклость производственных множеств фирм означает, что используемые технологии характеризуются либо постоянной, либо убывающей отдачей от масштаба. Это является необходимым условием реализации второй теоремы экономики благосостояния. Конкурентные рынки позволяют достичь любого распределения эффективного по Парето. Для поддержания различных распределений, эффективных по Парето, требуется перераспределить между потребителями начальные запасы.

Производственные возможности. Рассмотрим модель экономики с двумя видами выпускаемой продукции. Эта модель может быть распространена на случай многих товаров. Предположим, что производятся два товара. Если все ресурсы направляются на производство товара 1, то производство товара 2 равно нулю, и наоборот. В промежутках между этими крайностями производятся различные количества товара 1 и товара 2. На рисунке 9.6. отображены разнообразные комбинации этих двух товаров. Это множество возможных наборов двух производимых товаров известно как множество производственных возможностей. Граница множества производственных возможностей называется границей производственных возможностей.

Форма множества производственных возможностей зависит от природы лежащих в их основе технологий. Если технологии производства двух товаров характеризуются постоянной отдачей от масштаба обеих применяемых факторов производства, то множество производственных возможностей принимает форму, ломаной, состоящей из двух отрезков прямой линии.

Наклон границы множества производственных возможностей измеряет предельную норму трансформации. Последняя показывает, сколько можно получить одного товара, пожертвовав некоторым количеством другого, то есть, переведя часть ресурсов из производства второго товара, в изготовление первого.

Граница производственных возможностей показывает технологически допустимые потребительские наборы, которые может произвести экономика. На какой структуре набора товаров следует остановиться? Чтобы ответить на этот вопрос, рассмотрим эффективные по Парето способы осуществления выбора между этими технологически допустимыми потребительскими наборами. Отметим, что каждому такому набору соответствует определенная комбинация применяемых факторов производства, а значит и отраслевая структура нашего гипотетического хозяйства.

Эффективность по Парето. Обозначим совокупные потребительские наборы через и . Это означает, что в наличии для потребления имеются единиц товара 1 и единиц товара 2. Зная общее количество каждого товара, можно нарисовать ящик Эджуорта, как на рисунке 9.7.

При заданном ( , ) множество потребительских наборов, эффективных по Парето, будет множеством такого же рода, которое было рассмотрено в предыдущем параграфе. Как показано на рисунке 9.7., объемы потребления, эффективные по Парето, будут лежать на множестве Парето – линии касаний кривых безразличия. Это такие распределения, при которых предельная норма замещения каждого потребителя равна предельной норме замещения другого потребителя.

Указанные распределения являются эффективными по Парето в том, что касается решений о потреблении. Если индивиды могут просто обменять один товар на другой, то множество Парето описывает множество наборов, исчерпывающее выгоды обмена. Однако в экономике, где имеет место не только обмен, но и потребление, существует другой способ обменять один товар на другой, а именно: произвести меньше одного товара и больше другого.

Множество Парето описывает множество наборов, эффективных по Парето, при заданных начальных количествах товара 1 и 2. Но в экономике, где имеется производство, сами эти исходные количества могут быть выбраны из множества производственных возможностей. Какие варианты выбора из множества производственных возможностей будут эффективными по Парето?

В точке распределения, эффективного по Парето, предельная норма замещения (MRS) потребителя А должна равняться предельной норме замещения потребитель В. Иными словами, пропорция, в которой потребитель А хотел бы обменять один товар на другой, должна быть равна пропорции, в которой потребитель В готов обменять один товар на другой.

Предельная норма трансформации (MRT) измеряет пропорцию, в которой один товар «трансформируется» в другой. Разумеется, речь не идет о физическом превращении одного товара в другой, а всего лишь о переключении ресурсов с производства одного товара на другой.

Предположим, что экономика функционирует в точке, где MRS у одного из потребителей не равна MRT одного товара в другой. В таком случае указанная точка не может быть эффективной по Парето. В этой точке пропорция, в которой потребитель готов обменять товар 1 на товар 2, отличается от пропорции, в которой товар 1 может быть трансформирован в товар 2. Чтобы повысить благосостояние данного потребителя, нужно изменить структуру производства.

Когда у одного потребителя MRS отлична от MRT, всегда можно произвести перестройку структуры потребления и структуры производства, в результате которой благосостояние данного потребителя повысится. Как мы уже выяснили, в ситуации, эффективной по Парето, MRS каждого потребителя должна быть одной и той же, а из изложенного выше вытекает, что MRS каждого потребителя должна равняться MRT.

Рисунок 9.7. показывает распределение, эффективное по Парето. MRS у всех потребителей одинаковы, так как их кривые безразличия в ящике Эджуорта касаются друг друга. И MRS каждого потребителя равна MRT – наклону границы множества производственных возможностей.

Максимизации прибыли фирмой в конкурентной экономике. Ранее было отмечено, что механизм конкурентной экономики с максимизирующими прибыль фирмами и максимизирующими полезность потребителями приводит к распределению, эффективному по Парето. Рассмотрим детально, как это происходит.

Предположим, что в моделируемой нами экономике действует фирма, состоящая их двух индивидов. Имеется четыре товара: два фактора производства (труд индивида 1 и труд индивида 2) и два выпускаемых товара (одежда и фрукты). Экономика производит два выпуска - одежду С (clothes) и фрукты F (fruit) – и использует для этого два рода труда – труд индивида 1 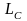, и труд индивида 2 . Если задана цена одежды , и цена фруктов и ставки заработной платы работника 1 и работника 2 и , то задача максимизации прибыли имеет вид:

(9.8)

при технологических ограничениях, описанных множеством производственных возможностей.

Допустим, что фирма сочтет оптимальным для себя в равновесии нанимать единиц труда работника 1 и единиц труда работника 2. Здесь нам необходимо ответить на вопрос. Каким образом максимизация прибыли определяет структуру производимого выпуска? Пусть выражение представляет издержки на труд. Запишем прибыль фирмы в виде:

. (9.9)

Это уравнение описывает изопрофитные (изо... гр. isos-равный, одинаковый; анг. profit - прибыль) линии фирмы, представленные на рисунке 9.8. Преобразовав это уравнение, получаем:

. (9.10)

Это уравнение показывает, что изопрофитные линии имеют наклон и точку пересечения с вертикальной осью . Поскольку согласно принятой предпосылке фиксирована, более высокая прибыль связана с теми изопрофитными линиями, которые пересекают вертикальную ось выше.

Если фирма хочет максимизировать прибыль, она вберет такую точку на границе производственных возможностей, чтобы изопрофитная линия, проходящая через эту точку, как можно выше пересекала вертикальную ось. Это подразумевает, что изопрофитная линия должна касаться границы производственных возможностей, то есть наклон границы производственных возможностей MRT должен быть равен наклону изопрофитной линии .

Рассмотренную задачу максимизации прибыли для случая одной фирмы можно распространить на произвольное число фирм. Каждая фирма, выбирающая наиболее прибыльный способ производства двух товаров, будет производить в точке, где предельная норма трансформации для любых производимых ею товаров равна отношению цен этих товаров. До тех пор пока цены на указанные два товара одинаковы для всех фирм, это остается справедливым, даже если множества производственных возможностей фирм совершенно различны.

Это означает, что в равновесии цены двух товаров измеряют предельную норму трансформации – альтернативные издержки на один товар, выраженные в другом товаре.

Взаимосвязь частных и общественных целей. В нашей экономике каждый индивид выбирает из числа доступных ему товарный набор, обладающий максимальной полезностью при ценах и . Такой оптимальный потребительский набор должен удовлетворять условию равенства предельной нормы замещения для двух товаров отношению цен этих товаров: MRS = / . В то же время максимизация прибыли фирмой достигается при условии равенства отношения цен предельной норме трансформации: / = МRT. Таким образом, удовлетворяются необходимые условия эффективности по Парето - MRS каждого потребителя равна МRT.

В такой экономике цены служат сигналом относительной редкости или ограниченности. Они показывают ограниченность в потреблении: насколько индивиды готовы сократить потребление одного товара ради приобретения некоторого количества другого. Цены указывают также на технологическую ограниченность: насколько следует сократить производство одного товара, чтобы произвести больше другого товара.

Рассматриваемая модель экономики позволяет увидеть взаимосвязь между индивидуальными частными целями максимизации полезности и общественными целями эффективного использования ресурсов. При принятых нами условиях преследование индивидами своих частных целей приводит к распределению, во всех отношениях эффективному по Парето. И наоборот, любое распределение, эффективное по Парето, при возможности соответствующего перераспределения начальных запасов – включая и собственность на фирмы, можно рассматривать как исход функционирования конкурентного рынка.

Каждому индивиду и каждой фирме нужно заботиться лишь о решении собственной задачи максимизации. Единственное, что им нужно для этой цели, - это знание товарных цен. При наличии ценовых сигналов, указывающих на относительную редкость товаров и ресурсов, потребители и фирмы располагают достаточной информацией для принятия решений, приводящих к эффективному размещению ресурсов. Последнее становится возможным благодаря свободе действий каждого участника. В этом смысле общественные проблемы, связанные с эффективным распределением ресурсов, могут быть децентрализованы и решены на индивидуальном уровне.