Закон убывающей предельной производительности переменного фактора производства.
Впервые закон убывающей предельной производительности был сформулирован американским экономистом Дж. Кларком33: в условиях, когда хотя бы один фактор производства остается неизменным, дополнительное приращение других факторов дает все меньший и меньший прирост продукции.
Увеличение количества переменного ресурса приводит сначала к возрастающему темпу роста выпуска (см. рис.5.1.) (МР↑, если L находится в промежутке от 0 до L1 ), затем темп роста замедляется ( ТР↑ МР↓, если L находится в промежутке от L1до L3), затем привлечение дополнительных единиц переменного фактора приводит к уменьшению выпуска(ТР↓, а МР< 0, если L> L3).
Очевидно, что общий продукт TP достигает своего максимума, когда предельный продукт становится равным нулю. До этого общий продукт имел положительный прирост (рос), теперь будет уменьшаться, значит при L = L3, TР достигает максимума. Графически средний продукт АР достигает максимального значения, когда пересекает кривую предельного продукта МС ( значение МС при L = L2).
Действие закона убывающей предельной производительности (убывающая ветвь параболы MP на графике – рис.5.1) объясняется тем, что один из факторов производства постоянен в рассматриваемом периоде времени (капитал). Ввод дополнительных единиц переменного фактора (труда) сначала позволяет эффективно использовать разделение труда, и каждый дополнительно нанятый работник обеспечивает прирост продукта на большую величину, чем предыдущий. Так будет продолжаться до тех пор, пока ресурс постоянного фактора производства не будет использован полностью. Тогда очередной нанятый работник станет все более «лишним», чем предыдущий (ему придется ждать своей очереди, чтобы поработать). То есть: постоянного фактора сначала слишком много относительно переменного. Затем их количества уравновешиваются, а затем постоянного фактора становится слишком мало (относительно переменного).
5.3. Двухфакторная производственная функция в краткосрочном периоде. «Изокванта», «изокоста». Оптимальная комбинация ресурсов.
Двухфакторная производственная функция имеет место в том случае, когда производитель может изменять количество двух факторов производства одновременно при постоянстве третьего фактора производства. Комбинация одного постоянного и двух переменных факторов производства может быть различной. Самая распространённая ситуация: выпуск продукции зависит от использования труда (L) и капитала (К) (переменные факторы производства).
Q = f (К, L) (5.9)
Предположим, фермер имеет возможность изменять количество используемых тракторов (К) и количество наёмных работников (L) при неизменном количестве посевных площадей (M). Производственная функция задана таблично (таблица 5.1.). В каждой клетке таблицы указано значение объёма производства зерна при использовании конкретного количества труда и капитала – QKL , в тоннах.
Таблица 5.1.
Пример двухфакторной производственной функции.
К L |
1 |
2 |
3 |
4 |
1 |
2 5 |
40 |
55 |
70 |
2 |
40 |
5 5 |
70 |
85 |
3 |
55 |
70 |
8 5 |
100 |
4 |
70 |
85 |
100 |
115 |
Нетрудно заметить, что одинаковый объём выпуска может быть достигнут при различной комбинации переменных факторов производства. Например, объём выпуска Q=70 тонн зерна может быть получен при использовании 1-й единицы капитала и 4 единиц труда, или при использовании 2-х единиц капитала и 3-х единиц труда и т.д. В таблице показаны линии одинакового объёма выпуска (изокванты), в пределах которых производитель может выбирать удобную ему комбинацию факторов производства.
Графическое изображение изоквант применяется для непрерывных производственных функций, для которых возможно бесконечно малое приращение количества переменного фактора. Так, фактор труд L измеряется не количеством рабочих, а рабочим временем (часами, минутами, секундами), так что фраза «полтора землекопа» приобретает реальный экономический смысл. График изокванты – проекция двухфакторной производственной функции в трёхмерном пространстве на плоскость факторов производства (см. рис.5.2).
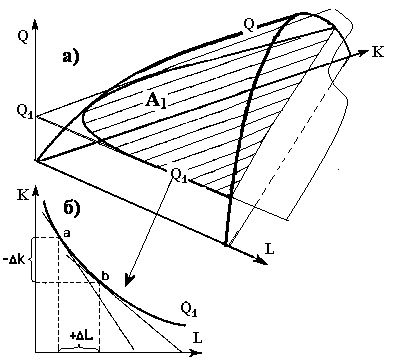
Рисунок 5.2. Построение изокванты.
Множество изоквант разного объёма выпуска в пространстве факторов производства представляют собой карту изоквант.