Линейные разностные уравнения, как инструмент построения математических моделей социально-экономических задач

Важным инструментом построения математических моделей социально-экономических задач, задач планирования, управления и сервиса являются дифференциальные уравнения (см., например, [1-4]).

Дискретным аналогом таких уравнений являются разностные уравнения [2]. В них операция дифференцирования заменяется конечной разностью , переводящей последовательность значений искомой функции в различные моменты времени в последовательность конечных разностей , Данное выражение называется разностью первого порядка. Аналогично строятся и разности более высоких порядков.

Разностным уравнением -го порядка называется уравнение вида

, 11\* MERGEFORMAT ()

где – фиксированное натуральное, a – произвольное целое числа, , , …, – члены некоторой числовой последовательности .

Решить разностное уравнение означает найти его общее решение, то есть все последовательности , удовлетворяющие уравнению 1.

В настоящей работе нами были рассмотрены две задачи экономики, приводящие к разностным уравнениям. В первой части рассматривается решение паутинообразной модели рынка, которая сводится к линейному разностному уравнению первого порядка. Построенное решение этого уравнения позволило сделать вывод о колебательном характере динамики цен. Во второй части изучена модель делового цикла Самуэльсона-Хикса, которая приводит к линейному разностному уравнению второго порядка.

Применение разностных уравнений первого порядка для исследования паутинообразной модели рынка

Постановка задачи состоит в следующем. Пусть некоторая производственная фирма определяет предложение товара в текущем периоде на основе цены , установившейся в предыдущем периоде: . Спрос на товар зависит от цены товара в данном периоде: . Требуется исследовать динамику цен и найти равновесную цену.

Для построения математической модели предположим, что функции спроса и предложения линейны относительно цены, причем с ростом цены предложение растет, а спрос падает: , . Здесь , , .

Равновесная цена находится из условия равенства спроса и предложения . В результате получается разностное уравнение . Переходя на один период по времени, придем к линейному неоднородному разностному уравнению первого порядка относительно цены

. 22\* MERGEFORMAT ()

Решение уравнения 2 представляет собой сумму общего решения соответствующего однородного уравнения и частного решения неоднородного:

, .

Здесь – постоянная, которая находится из условия задания начальной цены при :

.

Полученное решение позволило провести исследование динамики цены в зависимости от величин параметров и , характеризующих скорость изменения предложения и спроса в зависимости от цены .

1. Если , то последовательность цен будет сходиться к равновесному состоянию (Рисунок 1).

2. Если , то с течением времени цена будет удаляться от равновесного состояния (Рисунок 2).

3. При будут иметь место циклические колебания цены относительно равновесного состояния (Рисунок 3).

Рисунок 1. Последовательность изменения цены в случае

Рисунок 2. Последовательность изменения цены в случае

Рисунок 3. Последовательность изменения цены в случае

Решение линейных разностных уравнений второго порядка

Примером линейного разностного уравнения второго порядка является уравнение, описывающее модель делового цикла Самуэльсона-Хикса (см., например, [2]).

В этой модели используется так называемый принцип акселерации, то есть предположение о том, что масштабы инвестирования прямо пропорциональны приросту национального дохода , где – фактор акселерации, – величина инвестиций в период , , – величины национального дохода в -м и -м периодах.

Предполагается также, что потребление на данном этапе зависит от величины национального дохода на предыдущем этапе . Тогда условие равенства спроса и предложения приводит к разностному уравнению

, 33\* MERGEFORMAT ()

называемому уравнением Хикса.

Переходя на два периода по времени и вводя обозначения , , придем к линейному неоднородному разностному уравнению второго порядка

. 44\* MERGEFORMAT ()

Для решения соответствующего однородного уравнения составляется характеристическое уравнение , решение которого зависит от величины дискриминанта .

Частное решение неоднородного уравнения ищется в виде . Тогда и из уравнения 4 получаем

. 55\* MERGEFORMAT ()

Общее решение неоднородного уравнения найдется в виде суммы общего решения однородного разностного уравнения и частного решения неоднородного разностного уравнения 5.

Решение уравнения Хикса 3 было построено при конкретных значениях параметров , , .

Частное решение этого уравнения, согласно формуле 5, будет иметь вид

.

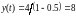Для построения общего решения соответствующего однородного уравнения было составлено характеристическое уравнение , имеющее комплексно-сопряженные корни

.

Следовательно, общее решение неоднородного уравнения примет вид

. 66\* MERGEFORMAT ()

Присутствие тригонометрических функций в решении 6 говорит о колебательном характере изменения национального дохода (Рисунок 4). При этом амплитуда колебаний с течением времени убывает.

Рисунок 4. Динамика изменения величины национального дохода