Алексеева О.В.

Ищенко И.Н.

МЕТОДИКА

ОБУЧЕНИЯ РЕШЕНИЮ ТЕКСТОВЫХ ЗАДАЧ

В НАЧАЛЬНОЙ ШКОЛЕ

Биробиджан, 2008

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение

высшего профессионального образования

«Дальневосточная государственная социально-гуманитарная академия»

Кафедра педагогики и методики начального образования

Алексеева Ольга Владимировна

Ищенко Инна Николаевна

МЕТОДИКА

ОБУЧЕНИЯ РЕШЕНИЮ ТЕКСТОВЫХ ЗАДАЧ

В НАЧАЛЬНОЙ ШКОЛЕ

Курс лекций

для студентов 3-5 курса, обучающихся по специальности 031200 «Педагогика и методика начального образования», и студентов 3-5 курса, обучающихся по направлению 540600, квалификация – бакалавр педагогики.

Биробиджан, 2008

УДК 372.851

ББК 74.262.21

М 545

Печатается по решению редакционно-издательского совета Дальневосточной государственной социально-гуманитарной академии

Авторы-составители: Алексеева Ольга Владимировна, к.п.н., доцент

Ищенко Инна Николаевна, к.п.н., доцент кафедры педагогики и методики начального образования ДВГСГА.

Алексеева О.В., Ищенко И.Н. Методика обучения решению текстовых задач в начальной школе. Курс лекций. – Биробиджан: Изд-во ДВГСГА, 2008. – 153 с.

Рецензенты: Жогло Л.Я. к.п.н., профессор кафедры педагогики и методики начального образования ДВГСГА.

Куликова С.И. зав. отделом контроля за качеством образования Комитета образования по ЕАО.

Данное учебно-методическое пособие предназначено для использования студентами 3-5 курса педагогического факультета, обучающимися по специальности – 540600 «Педагогика» и получающими квалификацию – бакалавр педагогики, а также студентами 3-5 курсов, обучающимися по специальности 031200 – «Педагогика и методика начального образования» при овладении методикой обучения решению текстовых задач младших школьников. Курс лекций является средством организации самостоятельной учебной деятельности студентов и соответствует образовательным стандартам по специальности – 540600 «Педагогика» и по специальности 031200 – Педагогика и методика начального образования.

© ДВГСГА, 2008

© Алексеева О.В., 2008

© Ищенко И.Н., 2008

Оглавление

Введение Обучение младших школьников решению текстовых задач. Методические приемы формирования понятия «задача» у младших школьников (известное, неизвестное, условие, вопрос). Основные этапы работы над текстовой задачей в начальной школе. Организация деятельности учащихся при обучении решению задач с пропорциональными величинами. Организация деятельности учащихся при обучении решению задач на движение. Тестовые задания для самоконтроля. Темы рефератов. Темы курсовых работ. Темы выпускных квалификационных работ. Заключение. Словарь терминов. Приложение.

5 8 29 49 86 105 121 126 126 128 129 130 134

Введение

В традиционном российском школьном обучении математике текстовые задачи всегда занимали особое место. С одной стороны, практика применения текстовых задач в процессе обучения во всех цивилизованных государствах идет от глиняных табличек Древнего Вавилона и других древних письменных источников, то есть имеет родственные корни. С другой — пристальное внимание обучающих к текстовым задачам, которое было характерно для России, — почти исключительно российский феномен.

Историю использования текстовых задач в обучении математике в русской школе условно можно разделить на несколько периодов.

Первый - до XVIII века. Массовое обучение математике ещё не сложилось. Потребности её применения в хозяйственной жизни удовлетворялись с помощью специально составленных математиками руководств — рецептов решения определённых видов задач. Ученики, подражая учителю, решали задачи на определенное «правило», при этом учащие мало заботились о сознательном усвоении учениками того или иного способа действия. Подтверждением тому служит фрагмент из книги И. Бёшенштейна (1514г.), в котором сначала дается «определение» тройного правила, формулируется правило, потом приводится задача и рецепт ее решения по правилу.

Второй - XVIII в. — середина XIX в. Это период обучения по «Арифметике» Л.Ф. Магницкого, период появления в обучении типовых задач «на бассейн», «простое тройное правило» и т.п. В то время-«задача была целью обучения, т.е. математику затем и учили, чтобы усвоить правила решения типичных задач». С.И. Шохор-Троцкий приводит фрагмент из «Арифметики» Л.Ф. Магницкого, из которого видно, что рецептурный стиль изложения материала, характерный для более ранних европейских источников, в первом российском учебнике арифметики еще не был преодолен.

Третий - конец XIX в. - начало XX в. Он характеризуется осознанием влияния процесса решения задач на усвоение математики детьми, на их развитие. В этот период в теории была признана роль задач как средства обучения. В русской школе начало этому периоду положили работы В.А. Латышева и С.И. Шохор-Троцкого.

Четвёртый - 30-е - 60-е годы XX в. Усиление значения текстовых задач как цели обучения. Появление большого числа работ по классификации и типизации задач. Разработка способов решения задач определённых типов. Возобладал узко практический подход к использованию текстовых задач. Тогда считалось, что обучать детей нужно с учетом возможностей применения изученных способов действий на практике или в дальнейшем обучении.

Пятый - с 60-х годов XX в. Это период конкретизации функций задач в обучении математике, отказ от типизации задач и разучивания способов решения задач определённых видов. Усиление роли задач как средства обучения. Стремление формировать у учащихся общие подходы к решению задач, то есть формировать с помощью задач важные общеучебные умения, связанные с анализом текста, выделением условий задачи и главного вопроса, составлением плана решения, постановкой вопроса и поиском условий, из которых можно получить на него ответ, проверкой полученного результата. Уточнение роли и места задач в обучении.

Выяснению роли задач в обучении посвящены работы многих психологов (Л.Л. Гурова, Е.И. Машбиц, Н.А. Менчинская, Л.М. Фридман и др.), дидактов (Я.И. Лернер, А.П. Сманцер и др.), специалистов по методике математики (М.А. Бантова, В.Ю. Гуревич, Ю.М. Колягин, Н.Б. Истомина, А.В. Белошистая, С.Е. Царева, Е.И. Лященко, М.И. Моро, К.И. Мешков, Д. Пойа, А.С. Пчелко, A.M. Пышкало, Н.К. Рузин, А.Д. Семушин и многие др.). Из дореволюционных методистов наибольший вклад в разработку этих вопросов внесли В.А. Латышев, С.И. Шохор-Троцкий, Е. Шпитальский.

До реформы математического образования в нашей стране (до 1967г.) текстовые задачи в начальном обучении математике выступали в основном как цель обучения. В этот период активно разрабатывались вопросы классификации задач и методики решения задач определённых видов (Н.И. Александров, Н.Н. Никитин, Г.Б. Поляк, Н.С. Попова, А.С. Пчёлко, Л.Н. Скаткин, Я.А. Шор и др.). Способы решения задач определённых типов и сами типовые задачи составляли значительную часть содержания курса математики. Эта часть должна была усваиваться детьми не хуже правил выполнения и свойств арифметических действий. На обучение решению типовых задач отводилась большая часть времени на уроке.

В методических пособиях для учителей основное внимание уделялось изложению различных классификаций задач и способов решений задач каждой группы, которые учитель должен сообщать детям в процессе обучения математике. Предполагалось, что, обучив учащихся умению распознавать вид (тип) задачи и выполнять усвоенный способ решения задач данного вида, школа научит детей решать любые задачи. Однако практика показала, что, привыкая решать задачи только известных им типов, учащиеся совсем не умеют осуществлять самостоятельный поиск даже в тех случаях, когда в решении нужно применить хорошо известные школьникам зависимости, но в ситуации, хотя бы немного отличающейся от типовых задач. Учащиеся, как отмечает М.А. Бантова, мало связывают решение задач с изучением других вопросов курса.

В действующих программах и методических пособиях (В.В. Давыдова, Л.В. Занкова, Н.Б. Истоминой, Л.Г. Петерсон и др.) особо подчёркивается роль текстовых задач как средства обучения детей. Причём наибольшее внимание авторы пособий уделяют использованию задач как одного из видов упражнений, обеспечивающих лучшее усвоение включённых в программу вопросов.

Суть современного развивающего подхода к обучению ребенка решению задач состоит в формировании у учащегося самостоятельной учебной деятельности, в том числе и в плане решения задач. Иными словами, речь идет не о том, чтобы научить ребенка узнавать и решать ограниченный круг типовых задач (сформировать навык решения типовых задач, как говорили в прежние годы), а научить ребенка решать любые задачи и притом самостоятельно. Исходя из жизненных реалий, мы понимаем, что невозможно научить этому всех детей с одинаковым уровнем успешности в одинаковые сроки. Сформировать у ребенка умения самостоятельной работы над задачей как учебной проблемой - вот одна из основных методических линий современной методики обучения математике в начальных классах.

Готовность будущего учителя к формированию умения младших школьников решать текстовые задачи предполагает развитие следующих умений:

• организовать работу учащихся, связанную с первичным анализом текста задачи;

• предвидеть и учесть в последующей работе ошибочный выбор учеником пути решения задачи;

• организовать фронтальную работу, вязанную с поиском пути решения задачи, выбрав для этой цели наиболее эффективный способ разбора и различные методические приемы;

• организовать работу над задачей после ее решения, используя для этой цели приемы преобразования и сравнения;

• организовать дифференцированную работу над задачей, используя для этой цели различные дифференцированные задания;

• проконтролировать правильность самостоятельно решенной учащимися задачи;

• определить причины ошибок, допущенными учащимися при самостоятельном решении задачи, организовать соответствующую работу по их разъяснению и устранению.

Данное методическое пособие посвящено рассмотрению теоретических и практических вопросов организации процесса обучения младших школьников решению текстовых задач в начальной школе.

Целью пособия является – помощь в формировании названных выше методических умений у будущих педагогов.

Курс лекций состоит из шести лекций по пяти темам: Обучение младших школьников решению текстовых задач. Методические приемы формирования понятия «задача» у младших школьников (известное, неизвестное, условие, вопрос). Основные этапы работы над текстовой задачей в начальной школе. Организация деятельности учащихся при обучении решению задач с пропорциональными величинами. Организация деятельности учащихся при обучении решению задач на движение.

После каждой лекции приведены задания практического характера. Также в пособии представлены задания для самоконтроля, темы рефератов, курсовых и выпускных квалификационных работ, заключение, словарь терминов и приложение.

Пособие предназначено для студентов педагогического факультета по специальности – 540600 «Педагогика», квалификации – бакалавр педагогики и по специальности 031200 – «Педагогика и методика начального образования», так же оно может быть использовано в качестве пособия по самообразованию для работающих учителей и организации занятий для слушателей курсов повышения квалификации работников образования.

Лекция,1.

Тема: Обучение младших школьников решению текстовых задач.

Цель: формировать представления студентов о теоретических и методических основах понятия «задача», о структурных элементах задачи и раскрыть приемы формирования понятия «задача» в различных авторских программах.

План:

1. Понятие «задача» и ее структурные элементы.

2. Виды текстовых задач.

3. Функции текстовых задач.

4. Подготовительная работа к обучению детей решать задачи.

5. Методические приемы формирования понятия «задача» в различных авторских программах.

1. Понятие «Задача» и ее структурные компоненты.

При обучении младших школьников решению задач уделяется большое внимание так, как:

1. в сюжетах отражена конкретная жизненная ситуация, знакомая ребенку, ему легко установить и осознать количественные отношения между объектами.

2. решение задач помогает осознать ребенку практическую значимость тех математических понятий, которыми он овладевает в начальном курсе математики.

3. в процессе решения задач у ребенка формируются умения, необходимые для решения любой математической задачи (выделять данные и искомые, условие и вопрос, устанавливать зависимость между ними, строить умозаключения, моделировать, проверять полученный результат).

Определим, прежде всего, что в методике начального обучения подразумевается под задачей. Под задачей в начальном курсе математики подразумевается специальный текст, в котором обрисована некая житейская ситуация, охарактеризованная численными компонентами, имеющими зависимость между собой. Таким образом, текст задачи можно рассматривать как словесную модель реальной действительности.

Пример. За 9 часов полета голубь может преодолеть 657 км. За какое время он, двигаясь с такой же скоростью, долетит от Петербурга до Москвы, если расстояние между городами 730 км?

В задаче описывается движение голубя. Любое движение описывается тремя величинами: пройденным расстоянием, скоростью и временем движения. В данной задаче известно, что расстояние между городами 730 км, дано расстояние, которое может преодолеть голубь за определенное количество времени. Необходимо найти за время, за которое он долетит между городами.

По мнению Н.Б. Истоминой, любое математическое задание можно рассматривать как задачу, выделив в нем условие, то есть ту часть, где содержатся сведения об известных и неизвестных значениях величин, об отношениях между ними и требование, то есть указание на то, что нужно найти [3].

Пример

1. Поставь знаки < > =, чтобы получились верные записи 3 5; 8 4.

Условие задачи: числа 3,5,8,4.

Требование: сравнить числа.

2. Реши уравнение х+4=9.

3. Выбери из данных прямоугольников те, из которых можно сложить квадрат.

В начальном курсе математики под понятием «задача» подразумевается арифметическая задача. Эти задачи формулируются в виде текста, в котором находят отражение количественные отношения между реальными объектами. Поэтому их называют «текстовыми», «сюжетными», «вычислительными». Основная особенность текстовых задач состоит в том, что в них не указывается какое именно действие (или действия) должно быть выполнено для получения ответа на требование задачи.

Таким образом, задача является носителем какой-либо познавательной информации и обладает следующими свойствами:

• проблемность, воздействующая на потребностно-мотивационную сферу учащегося и тем самым стимулирующая его деятельность;

• необходимость в интеллектуальных усилиях, организующая систематические умственные упражнения и прививающая «вкус» к интеллектуальному труду, а, следовательно, влияющая на развитие мышления;

• неизбежность преобразовательных действий с моделями задач, обеспечивающая усвоение предметного содержания задачи и способствующая развитию продуктивных форм мышления.

Структурные элементы задачи.

Структурными элементами задачи являются: условие, требование, данные и искомое.

Условие - это часть текста, в которой задана сюжетная ситуация, численные компоненты этой ситуации и связи между ними. В стандартной формулировке условие выражается одним или несколькими повествовательными предложениями.

Требование - это часть текста, в которой указана искомая величина (число, множество). В стандартной формулировке учебников начальных классов требование обычно выражено вопросом, начинающимся словом «сколько» и заканчивающимся знаком вопроса.

Данные - это, как правило, численные (числовые) компоненты текста задачи. Они характеризуют количественные отношения предлагаемой в задаче ситуации: значения величин, численные характеристики множеств и отношений между ними. Численные значения величин и численные характеристики множеств обычно обозначены числами. Численные характеристики отношений между ними могут быть обозначены не числом, а словом, например: «в два раза больше», «столько же, сколько в первом» и т. п, В этом случае дети могут «терять» данные и вообще не воспринимать эти численные характеристики как данные. Провоцируется такая ситуация тем, что все тексты в начальной школе содержат данные, выраженные численно, а тексты задач первого года обучения содержат только численные данные. В этом случае ребенок (особенно плохо читающий) «выхватывает» числа из контекста, и выполняет с ними действия практически независимо от ситуации, заданной в условии (чаще всего ориентируясь на «ключевое» слово: улетели, дали, вместе, принесли и т.п.).

Искомое. Нахождение искомого в численном выражении обычно является конечной целью процесса решения арифметической задачи.

В дальнейшем дети будут сталкиваться с другими видами задач, в частности с задачами геометрического характера: на доказательство, на построение, где искомым является либо сам процесс решения (задачи на доказательство), либо результат этого процесса, выраженный не в численных характеристиках (фигура в задаче на построение; буквенное выражение в алгебраической задаче). Задачи последнего вида часто встречаются в учебнике Л.Г. Петерсон, Н.Б. Истоминой. Приведем пример задачи, где процесс ее решения приводит к численному результату, который не является целью решения задачи, а лишь косвенно используется для характеристики неизвестного: «Если цену учебника уменьшить в 3 раза, то получим цену блокнота. Блокнот в 3 раза дороже тетради. Краски в 9 раз дороже тетради. Хватит ли денег, которые мама дала для покупки учебника, на покупку красок?» (учебник Н.Б. Истоминой).

Ответ к данной задаче предполагается в виде: «Денег на покупку красок хватит». Чтобы получить этот ответ, следует установить соотношение между ценами и фактически выразить цену красок в количестве «единичных цен», за которые нужно принять цену тетради.

В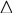 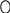учебниках математики для начальной школы встречаются задачи, имеющие различные конструкции. Рассмотрим их.

Обозначим схематически условие , а требование . Задача может иметь одну из конструкций: 1, 2 или 3:

1 .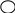

1) Дети пошли в поход. Было 18 мальчиков и 10 девочек. Сколько детей пошло в поход?

2) В один бидон вмешивается 32 л. воды, а во второй – на 12 л. меньше. Найди емкость двух бидонов вместе.

3) Дети посадили 4 куста малины, 5 кустов смородины, а крыжовника столько кустов, сколько малины и смородины вместе. Сколько вместе кустов посадили дети?

4) В оркестре 8 скрипок, а альтов – на 2 меньше. Когда к альтам добавили еще несколько инструментов, то их в оркестре стало 9. Сколько альтов добавили?

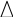
2.

5) Сколько марок подарил Петя, если Сереже он подарил 8 марок, а Коле 5 марок?

6) Сколько пассажиров совершало полет, если в самолете было 25 женщин, мужчин на 15 человек больше, чем женщин, а детей на 10 человек меньше, чем женщин?

7) Сколько карандашей в двух одинаковых коробках, если в одной 2 десятка карандашей?

8) Сколько нужно колес для двух трехколесных велосипедов?

3 .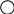

9) Мама испекла 20 пирожков. Сколько пирожков осталось после того, как за ужином съели 15 пирожков?

10) В магазине продали 22 ящика с помидорами. Сколько ящиков с помидорами было, если осталось продать 8 ящиков?

11) Белоснежка вырастила 14 астр и 20 гвоздик. Сколько цветов осталось у Белоснежки после того, как она подарила гномам 7 цветов?

12) Когда отцу было 40 лет, сыну было 12. Найди возраст сына, когда отцу было 52 года.

Такие тексты в методике обучения математике младших школьников принято называть трансформированными. Работа с такими текстами является наиболее полезной с точки зрения обучения решению задач, поскольку именно такие тексты учат ребенка внимательно читать и анализировать задачу, целенаправленно устанавливать связи между данными и искомым с целью осознанного выбора действия. Работа над такими задачами - и есть та перспективная линия, имея в виду преемственность обучения математике.