§ 53. Особенности динамики систем стабилизации частоты вращения (режимов обработки)

Анализ динамики системы с обратной связью по напряжению при изменении задающего воздействия. Качество процессов управ­ления в системах автоматики должно оцениваться статизмом, а также по поведению системы в переходном процессе: при измене­нии задающего и приложении возмущающего воздействий.

Для механизмов деревообработки, приводы которых работают в режиме стабилизации частоты вращения, мощности резания, постоянства массы дозируемого материала и других регулируемых параметров, характерен скачкообразный рост или сброс нагрузки.

Предположим, что изменения задания невелики и систему можно считать линейной в области возможных отклонений пере­менных от установившегося предшествующего режима. При рас­смотрении переходных процессов полагаем возмущающие воздейст­вия равными нулю (М_с = 0).

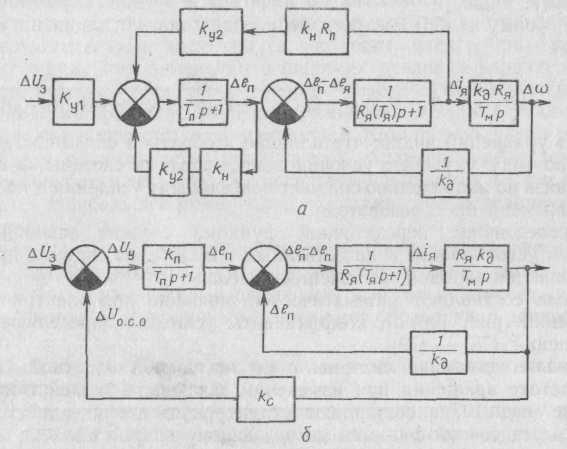
Рис. 109. Структурные схемы систем П—Д с обратной связью:

а — по напряжению; б — по частоте вращения

На основании принципиальной схемы (см. рис. 107, а) составим структурную схему системы (рис. 109, а) без учета обратной связи по току.

При математическом описании системы уравнения записываем в приращениях:

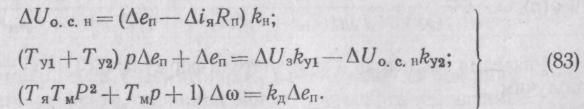Двигатель представляется состоящим из двух звеньев:

Из уравнений (83) получим

где Т_у1 = L_y/R_y1; Т_у2 = L_y2/R_y2 — постоянные времени обмоток ОУ1 и ОУ2; k_y1= e_п/( i_y1—R_y1); k_y2= e_п/( i_y2— R_y2); k_н = = U_осн/ U_п— коэффициенты; усиления обмоток 0У1, ОУ2 и обратной связи по напряжению.

Из уравнений (84), (85) находим дифференциальное уравнение системы

Из уравнения видно, что коэффициент при первой производной уменьшается при увеличении k_c. Следовательно, отрицательная обратная связь ухудшает условия демпфирования системы и при больших k_c приводит к нарушению устойчивости.

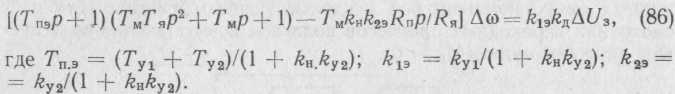
Из формулы (86) следует, что передаточная функция по управ­лению

Из уравнений видно, что наличие в обратной связи составляю­щей по току ухудшает условия демпфирования системы, а обрат­ная связь по напряжению снижает коэффициент усиления и постоян­ную времени преобразователя.

Исследование передаточной функции служит основой для оценки устойчивости и качественных показателей системы при ис­пользовании методов, изложенных в главе 1.

Если составляют математическое описание при электрическом сложении (рис. 106, а), коэффициенты усиления определяются из уравнений (78) — (79).

Анализ динамики системы с отрицательной обратной связью по частоте вращения при изменении задающего воздействия. На основе рис. 107, в составляют структурную схему (рис. 109, б). Для передаточной функции по задающему воздействию

W₃(p) = (p)/ U₃(p).

Составим дифференциальное уравнение замкнутой системы

§ 54. Оптимизация динамических свойств автоматических систем управления

Постановка задачи и критерии оптимальности. При автомати­зации производства в деревообработке приходится считаться с тем, что исполнительные элементы (в частности, электроприводы) ра­ботают в условиях изменения в широких пределах характеристик технологического процесса и внешних воздействий на систему уп­равления, которые заранее непредсказуемы. В этих условиях си­стема должна автоматически изменять и формировать закон управ­ления для оптимального (наилучшего) управления объектом (ре­жимом обработки деталей). Такие системы называются адаптив­ными. Наибольшее применение получили самонастраивающиеся системы.

Рассмотрим постановку задачи оптимального управления, кри­терии оптимальности и определение алгоритмов оптимизации управления динамическими системами, к которым относят, в част­ности, системы регулирования режимами обработки в деревообра­ботке.

Объект управления характеризуется вектором состояния =(х₁, х₂, . . . , х_n).

Составляющие вектора могут иметь различную природу и сущ­ность: для двигателя — момент, мощность, частота вращения, угол поворота вала; для сушильного барабана — влажность, темпера­тура; для предприятия — отдельные показатели плана.

Передаточная функция замкнутой системы из (87) будет

К_объекту прикладываются следующие воздействия: управляю­щие = (и_1, и₂, . . . , и_т), возмущающие = (z_1, z₂, z, . . . , z_k). На составляющие вектора состояния и управляющие воздействия почти всегда накладываются ограничения:

Разделив числитель и знаменатель формулы (88) на (1 + k_сk_пk_д), получим

x₁ X₁, x₂= X₂, . . . , x_n X_n;

u₁ U₁, u₂ U₂, . . . , u_m U_m.

Например, если рассматривать напряжение на зажимах двига­теля и его скорость, то они не могут превышать допустимые.

Изменение вектора управления U во времени или в пространстве координат называется алгоритмом управления.

Возмущающие воздействия, мешающие достижению цели уп­равления, называют помехами.

Векторы , , связаны некоторой зависимостью. Мы будем рассматривать только объекты, в которых связь между векторами

может быть записана в виде системы дифференциальных уравнений: dx_i/dt = f_i(x₁, х₂, . . . , х_n, u₁, u₂, . . . , u_m, z₁, z₂, . . . , z_k),

где i= 1, 2, . . . , n.

В векторной форме ( /dt = f ( , , ), где функции f_i опреде­лены для любых , .

Цель управления состоит в нахождении алгоритма управления U, который доставляет экстремум функционала, например:

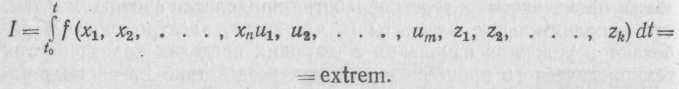
Каждому управлению U (t), заданному на отрезке t₀ t t_n и в области управления и U, будет соответствовать определен­ное численное значение I. Таким образом, из возможных (t) нужно найти такое, которое доставляло бы I экстремальное зна­чение.

Рассмотренная задача в общем виде распадается на ряд частных задач, соответствующих различным критериям оптимальности (це­лям управления).

_3адача о максимальном быстродействии. Если f ( , , )=1, то

Критерий оптимальности I означает минимум времени перехода координат объекта из положения _о в положение ₁ при соответству­ющих ограничениях или без них. Задача синтеза системы по интегральным критериям качества переходных процессов. Если f ( , , )=х², то

где х — отклонение координаты от установившегося значения.

Интегральный критерий качества переходных процессов харак­теризует минимум составляющей свободного движения системы и применяется для косвенной оценки переходного процесса в замк­нутых системах управления. Он оценивается площадью, ограничен­ной кривой х². Чем меньше площадь, тем быстрее затухает процесс.

Применение обобщенного интегрального критерия I позволяет получить достаточно быстрые и плавные переходные процессы:

В этом критерии первый член оценивает отклонение х, а после­дующие члены — производные от х.

Задача может быть прямой и обратной. В первом случае при заданных весомых коэффициентах ₁, ₂, . . . , _п-1 вычисляют I, во втором — выбирают параметры замкнутой системы, обеспечи­вающие I = min при заданных ₁, ₂, . . . , _п-1.

Задача аналитического конструиро­вания регулятора. Если

то критерий оптимальности

В этом случае находится закон изменения U (t), обеспечиваю­щий I = min. Зная алгоритм (t) или (t), можно сконструиро­вать регулятор, который бы его вырабатывал.

Задача ограничения энергетических по­казателей. Формулировка критерия" оптимальности: найти максимум функционала

Это равносильно определению максимального угла поворота вала двигателя = I₁ при ограничении количества тепла, выде­ляющегося в якоре Q = I₂.

Определение алгоритмов управления при рассмотренных кри­териях может быть выполнено с использованием классических ме­тодов вариационного исчисления для задач с открытыми областями изменения X и U (малые отклонения и от их уста­новившихся значений); принципа максимума Понтрягина при замкнутых областях изменения X и U, когда коорди­наты векторов и могут находиться на границах областей; ди­намического программирования Беллмана при замкнутых обла­стях и сложных критериях, требующих применения для расчетов ЭВМ.

Синтез разомкнутых систем, оптимальных по быстродействию. Оптимальное управление по быстродействию в физическом смысле связано с балансом энергии в объекте. Мощность и работа связаны уравнением N = A/t; A=A₃+A_n; t=A₃/N + A_п/N,

где Аз — запасенная в объекте энергия; А_п — полезная работа.

Несоответствие запасенной энергии номинальному режиму вы­зывает изменение управляемых координат. С увеличением мощ­ности процессы накопления энергии или вещества ускоряются. Таким образом, в процессе управления по быстродействию необ­ходимо обеспечить достаточную мощность для покрытия несоот­ветствия запасенной энергии или веществами требуемой полезной

работы. Эта задача решается соответствующим формированием алгоритма управления.

Для нахождения оптимальных управлений по быстродействию наиболее широко применяют принцип максимума, которой заклю­чается в следующем. Если объект управления описывается дифференциальным урав­нением в векторной форме (d )/(dt) = f ( , ), на уравнение на­ложено ограничение | и | U_max, и критерий быстродействия вы­ражается уравнением

Необходимо определить вектор (f), который обеспечивает оптимальное время перехода объекта из состояния (t₁) в состоя­ние (t₂). Предполагается, что f ( ₁ ) определена для любых значений х Х, непрерывна и дифференцируема по всем перемен­ным х₁, х₂, . . . , х_п. Управление принадлежит области и U и классу кусочно-непрерывных функций с разрывами первого рода. Для решения этой задачи записывается функция Гамильтона

Приведем систему к нормальному виду:

Согласно принципу максимума необходимо, чтобы Н = max. Для этого требуется, чтобы и =U_max при _i (t) >0 и и =U_min при _i (t) <0. Максимум H ищут только по управляющим сигна­лам и с учетом ограничений и U_max, а остальные переменные (t) и (t) считают независимыми от и. Следовательно, и (t) = = sign _i (t) U_max. Отсюда следует, что нужно определить, сколько раз _i (t) меняет знак, т. е. сколько корней имеет функция _i (t).

Управляющее воздействие скачкообразно изменяет значение от + U_max до U_max. Моменты изменения знака функции управления называют моментами переключения. При этом уп­равлении обеспечивается минимальное время перехода.

Для полного определения вектора управления необходимо найти границы участков, по которым происходят переключения управ­ления (± U_max) (рис. 110, а). Методы изложены в специальной ли­тературе [1, 40].

Пример. Объект управления (двигатель постоянного тока, уп­равляемый тиристорным преобразователем) описывается дифферен­циальным уравнением

Требуется перевести объект из состояния х = 0х = 0 при t = 0 в состояние х = х_п х = 0 за минимальное время. На управляющее воздействие наложено ограничение | и | U_max . Электромеханиче­ская постоянная времени Т₁ = 0,5 с, электромагнитная постоянная времени Т₂ = 0,3 с; k = 2,15; | и | U_max = 127; х_п = 230 услов­ных единиц.

Вспомогательные переменные должны удовлетворять следую­щей системе дифференциальных уравнений: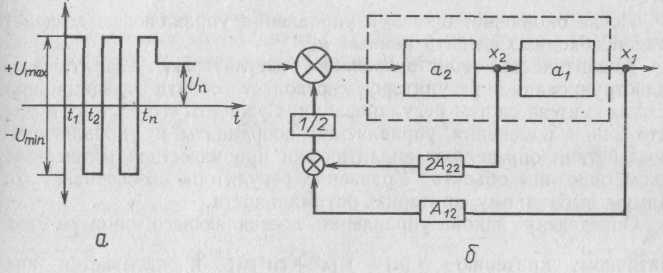

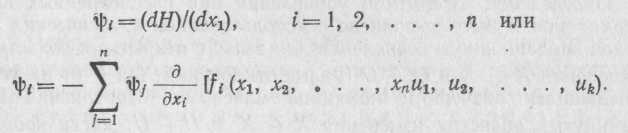
Рис. 110. Результаты синтеза системы оптимального управления:

a — график переключения: б — структурная схема

Составим уравнение для сопряженных переменных:

Найдем решения для и :

Функция Гамильтона

Так как (Т₁ + Т₂) 2 Т₁Т₂, запишем систему уравнений

Рассматривая члены, зависящие от и, и значения , , находим

Критерий оптимальности

Гамильтониан имеет максимальное значение, если и = U_max и знак и_max должен изменяться столько раз, сколько меняет его функция

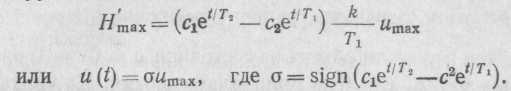
Функция при любых значениях с₁ и с₂ изменяет знак не более одного раза, а алгоритм оптимального управления состоит из двух интервалов управления

и (t) = t_max = ± U_max, где = ±1.

После окончания процесса управления управляющее воздейст­вие необходимо сделать равным и₃.

Аналитическое конструирование регуляторов. Аналитическое конструирование регуляторов позволяет обойти традиционные схемы синтеза систем регулирования. Сущность его состоит в том, что закон изменения управляемой координаты и управляющего воздействия определяют аналитически при известном математиче­ском описании объекта. Уравнение регулятора обеспечивает ми­нимум выбранному критерию оптимальности.

Определение закона управления, доставляющего минимум квад­ратичному критерию и называется ана­литическим конструированием регулятора. Стабилизация систем относительно положения равновесия с помощью законов управле­ния, обеспечивающих этот минимум, называется оптимальной стабилизацией. Обе задачи можно решать мето­дами классического вариационного исчисления, принципа макси­мума, динамического программирования.

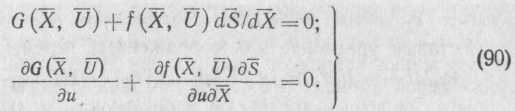
Из системы уравнений (90) следует закон управления

Пример. Объект описывается системой нормальных дифференци­альных уравнений:

Рассмотрим применение метода динамического программирова­ния для аналитического конструирования регулятора, который описывается системой уравнений Беллмана:

Требуется определить закон управления и = f (x₁, x₂). Составим функциональные управления Беллмана (90):

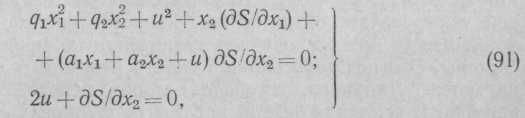
где а₁, а₂ — коэффициенты, определяемые параметрами объекта; q₁, q₂ — весомые коэффициенты квадратичного функционала.

Из второго уравнения определится закон управления:

Подставив (92) в первое уравнение системы (91), получим

Для линейных объектов управления и квадратичных крите­риев оптимальности функция S представляет положительно-опре­деленную квадратичную форму: S= с частными производными:

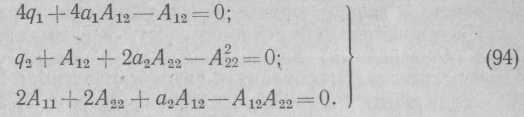
Решив систему уравнений (94), определим:

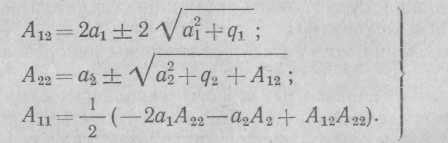
Подставив в (93) значения dS/dx_i и приравняв нулю члены при одинаковых степенях х₁ и х₂, составим систему алгебраических уравнений для определения А₁₁, А₁₂, А₂₂:

Из возможных значений А₁₂А₂₂А₁₁ выбирают положительные, так как функция S должна быть положительно-определённой при устойчивом решении.

Закон управления (рис. 110,б):

Выражение (95) показывает, что регулятор состоит из жестких обратных связей по координатам х₁, х₂ с коэффициентами усиле­ния k₁ = A₁₂, k₂ = А₂₂. Важным свойством структуры, получен­ной в результате оптимизации, является способность сохранять устойчивость при бесконечном увеличении коэффициента усиления системы. Это подтверждается тем, что решение задачи базируется на методе Ляпунова, согласно которому система асимптотически устойчива, если для нее можно найти функцию Ляпунова, т. е. знакоопределенную положительную функцию, производная ко­торой есть знакоопределенная отрицательная функция.