§ 48. Регулирование потока и запаса материала

Регулирование потока. Процесс деревообработки невозможен без удерживания некоторого количества материала и полуфабри­катов. Место хранения материалов может быть ограничено имею­щейся свободной площадью или объемом.

Количество накопленного материала не может изменяться одно­временно с изменением материального потока, обычно для этого требуется некоторое время.

Предположим, что в промежуточной области производственного цикла накоплено G (t) тонн материала (рис. 96, а). Поступление материала составляет Q₁ (t) т/ч, а потребление или отводимый поток — Q₂ (t) т/ч. Рост запаса G (t) будет при условии Q₁ (t) > > Q₂ (t), уменьшение — при Q₁ (t) <Q₂ (t). Скорость изменения

Рис. 96. Схемы потоков материалов и запаса:

а — материального потока; б — управления запасом; в — технологической линии с n-сборниками; г — характеристики изменения запаса по n-сборникам; д — изменение за­паса в бункерах

запаса равна результирующей массной скорости и определится из уравнений:

Q₁(t) — Q₂ (t) = Q(t);

[dG (t)]/dt = Q (t) = Q₁(t) — Q₂ (t).

Зависимость между текущим запасом G (t) и результирующей масс­ной скоростью

Таким образом, изменение запаса всегда будет интегралом от изменения результирующего потока Q (t) и, преобразовав по Лапласу уравнение (75), получим

pG_p—G(0)= Q(p)

или

pG(p)—G(0) = Q₁(p)—Q₂(p). (76)

Операция интегрирования в уравнении (75) определяет процесс изменения запаса при G₁ (t) G₂ (t) как идеальное интегрирующее звено. Передаточная функция из уравнения (76) определяет модель процесса изменения запаса

G (р) = 1/p [ Q₁ (p)—G (0)] W (p) = [G (p)]/[ Q (p)] = 1/p.

Перемещения материалов в соответствии с типовыми моделями структуры потоков относятся к процессу идеального вытеснения. Поэтому математическое описание изменения запаса следует до­полнить структурной моделью идеального вытеснения, представ­ляющей собой звено чистого запаздывания W₃ (р) = е^—p . Общее уравнение будет (рис. 96, б)

где W_п —общая передаточная функция; = l/v, l—расстояние между рассматриваемыми точками; v — скорость перемещения

потока.

В деревообрабатывающей промышленности многие технологи­ческие системы содержат конвейерные устройства, технологиче­ское оборудование и емкости или промежуточные сборники. Это характерно для производств: древесностружечных и древесново­локнистых плит, стройдеталей, покрытий мебельных щитов и для других участков, где используют автоматические или полуавтома­тические линии.

В этих условиях важно изучение правил, которые определяют изменение потока материала между емкостями или сборниками для верного формирования рекомендаций по управлению матери­альными потоками на данных объемах сборников или для оптималь­ного выбора объема сборников, бункеров. Сборники или бункера между технологическими операциями могут решать задачу компен­сации возмущений по нагрузке.

При управлении процессами перемещения необходимо иметь в виду, что если регулируется запас, то материальный поток бу­дет переменным и наоборот, если регулируется материальный по­ток, переменным будет запас.

сборника или запаса другого типа при регулировании подводимым потоком:

Управление потоком на участке технологической линии харак­теризуется подводимым потоком Q₁ (t) и отводимым потоком Q₂ (t). Постоянство запаса или удерживающей способности характери­зуется уравнением

Если отводимый поток пропорционален запасу Q₂ (t) — kG (t), связь между подводимым и отводным потоком может характеризо­ваться передаточными функциями:

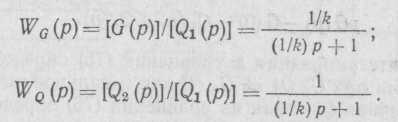
Структурная схема, характеризующая процесс управления по­током по пропорциональному закону, представлена на рис. 96, в.

При равенстве коэффициентов k₁ = k₂ = . . . = k_n = k связь запаса G_n (p) от потока Q_1,1 запишется

Рассматривая технологическую линию можно видеть, что она состоит из ряда сборников, бункеров или транспортных механиз­мов, перемещающих материал, структурную схему можно предста­вить рис. 96, г. Передаточная функция запаса n-го сборника W₃ (p) от подводимого к нему потока будет [13, 33]:

Аналогично запишется соотношение между отводимым Q₂ (p) ^и подводимым Q₁ (p) потоками:

Приняв масштаб шкалы времени как а = kt, и отношение p/k = , уравнения примут вид:

Из построенных характеристик 1—5 по уравнениям (77) для технологической системы, состоящей из пяти одинаковых бунке­ров или емкостей (рис. 96, д), можно сделать вывод [13, 33], что чем дальше емкость от точки приложения возмущения, тем меньше влияние на запас как в сторону пополнения, так и уменьшения его.

Изменение подчинено экспоненциальному закону. Максималь­ное значение запаса находят из уравнения

Достигается максимальный запас по емкостям или складам, последовательно расположенным в технологической схеме в раз­личное время и имеющим различную величину.

Регулирование запаса. На величину запаса G оказывают влия­ние подводимые и отводимые потоки, суммарное воздействие ко-

торых характеризуется величиной Q(t) = . Для случая двух потоков

Q(t) = Q₁(t)—Q₂(t).

Следовательно, управлять запасами может один из указанных по­токов. Динамические характеристики изменения запаса будут за­висеть от принятого способа управления.

Возможны три варианта регулирования запаса:

1. непрерывное регулирование — закон управления форми­ руется как функция отклонения = G₃ (t) — G (t). В этом случае величину запаса контролируют непрерывно и непрерывно форми­ руются и выдаются управляющие воздействия;

2. величину запаса контролируют через равные определенные промежутки времени, формируется управляющее воздействие по величине рассогласования е и выдается управляющее воздействие на соответствующий поток. На отрезке времени между измере­ ниями величина воздействия остается постоянной;

3. величина запаса может регулироваться позиционно с соблю­ дением верхней и нижней допустимых границ отклонения запаса от заданного ± _зад.