Глава 8

ТЕХНОЛОГИЧЕСКИЕ ОСНОВЫ АВТОМАТИЗАЦИИ И ОБЪЕКТЫ УПРАВЛЕНИЯ

§ 45. Характеристика производственных процессов и производств

На предприятии осуществляется сложный процесс превраще­ния материалов, сырья, полуфабрикатов в готовую продукцию. Выполнение этого процесса требует выполнения ряда функций, совокупность которых принято называть производственно-хозяйст­венной деятельностью предприятия.

В соответствии с производственно-хозяйственными функциями предприятие (систему) можно разбить на подсистемы, т. е. части предприятия, выполняющие определенные функции (рис. 85).

Производство готовой продукции сосредоточено в специальных цехах, совокупность которых называют основным производством предприятия.

Производство вспомогательного оборудова­ния инвентаря, инструмента, выполнение ремонтных работ рас­положено в цехах вспомогательного производства. На всех круп­ных предприятиях можно видеть функциональные подразделения: ремонтное, энергетическое, транспортное, инструментальное.

Техническая подготовка производства предусмат­ривает конструирование новых и модификацию выпускаемых из­делий, а также разработку технологии производства и нормирова­ние расхода ресурсов.

Материально-техническое обеспечение определяет число и размеры партий закупаемых сырья и материа­лов, обеспечивает оперативную связь с поставщиками, оформляет документы на получение. Другая задача — складирование мате­риалов, их хранение и выдача в соответствии с регламентом или по требованию.

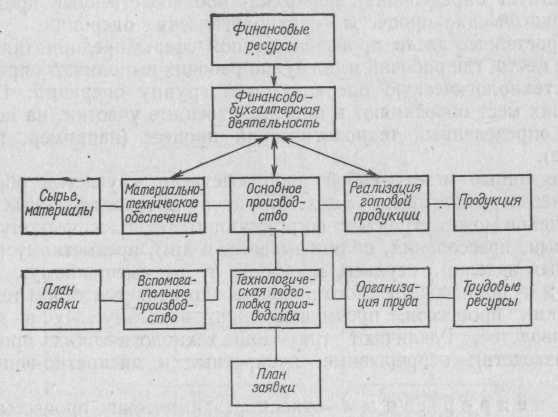
Рис. 85. Схема основных взаимосвязей функций производственно-хозяйст­венной деятельности предприятия

Организационно-трудовая подготовка производства — набор и обучение кадров, расстановка, нормиро­вание и организация труда, решение вопросов оплаты, материаль­ного и морального стимулирования кадров.

Финансово-бухгалтерская деятельность объединяет анализ, учет, документирование всех операций, связан­ных с закупкой сырья, материалов, полуфабрикатов, реализацией продукции, начисление заработной платы, контроль использова­ния материальных ценностей.

Реализация готовой продукции включает складирование, вывоз, организацию погрузки и отправки, оперативную связь с за­казчиком.

Центральное звено предприятия — основное производство, где осуществляется производственный процесс. Простейшим элементом производственного процесса считают технологическую операцию.

Технологическая операция — любое механиче-

ское или физико-химическое воздействие на материалы (фрезеро­вание, пиление, установка детали, смешивание компонентов). Тех­нологический процесс — совокупность технологических операций, осуществляемых на определенном оборудовании (сборка изделий, изготовление заготовок и т. д.), результатом которых яв­ляется полуфабрикат или готовое изделие.

Производственный процесс — связанная материаль­ными потоками совокупность технологических процессов, обеспе­чивающих получение конечного изделия (от производства деталей до сборки готовой мебели и др.). Таким образом, в производстве существует определенная иерархия: производственный процесс — технологические процессы — технологические операции.

Простейшее звено производственной сферы предприятия — ра­бочее место, где рабочий или группа рабочих выполняют определен­ную технологическую операцию или группу операций. Группы рабочих мест объединяют в производственные участки, на которых идет определенный технологический процесс (например, прессо­вание).

Связанные между собой производственные участки образуют производственное звено — цех. Структура производственных участ­ков, цехов может строиться по принципам: технологическому (стро­гальный, прессования, облицовывания и др.), предметному (строи­тельных изделий, стульев, шкафов и т. д.), смешанному.

Тип производственного процесса определяется типом техноло­гических процессов, преимущественно используемых в данном производстве. Различают три типа технологических процессов (производств): непрерывные, дискретные и дискретно-непрерыв­ные.

К непрерывным относятся химические процессы, про­ цессы производства энергии, сушка стружки в барабанных сушил­ ках, конвейерные сушилки и т. д. При этом поступление сырья, обработка и выход продукции происходят практически постоянно в процессе работы установки.

Параметры, характеризующие эти процессы,— температура, давление, расход вещества или энергии и т. п.

При дискретных процессах обрабатываемые изделия по­даются на вход и выдаются на выходе отдельными порциями. Ха­рактерный признак — наличие процесса сборки. Определяет эти процессы число деталей, узлов, изделий на различных стадиях про­цесса (изготовление мебели, строительных изделий, лущение и т. д.).

Дискретно-непрерывные процессы объединяют свойства двух процессов — дискретного и непрерывного. В дерево­обработке характерным примером дискретно-непрерывного произ­водства является производство древесностружечных и древесново­локнистых плит.

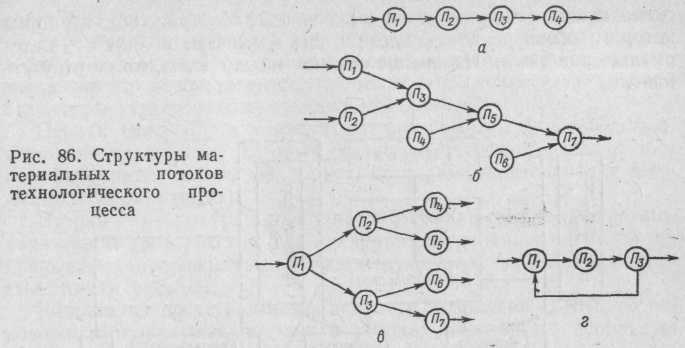
Структура производственного процесса характеризуется сово­купностью технологических операций, подчиненных логически упо­рядоченному их соединению, что образует технологическую схему, связанную определенным материальным потоком. Технологическая

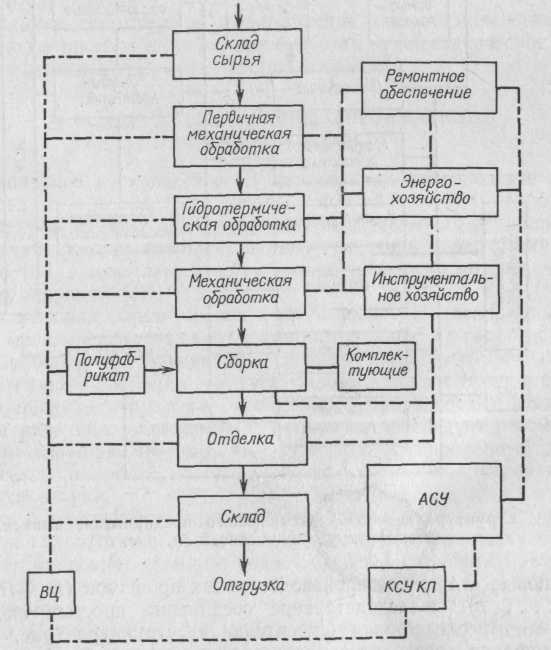
Рис. 87. Структура деревообрабатывающих предприятий, выпускающих

штучные изделия: — — основные связи производственных цехов;

связи вспомогательных цехов с основным производством;— — —информа­ ционные связи в АСУ производства; КСУ КП — комплексная система уп­ равления качеством

схема может быть представлена в виде графа (рис. 86), вершины которого обозначают технологические элементы, а линии — мате­риальные потоки. Изменение потока между элементами отсутст­вует.

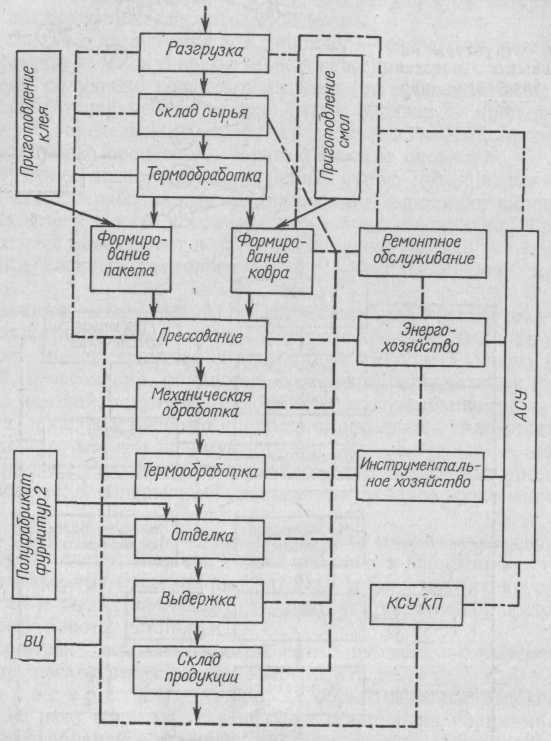
Рис. 88. Структура деревообрабатывающего предприятия, выпускающего плиты (фанеру) (виды связей см. рис. 87)

Типовые структуры производственных процессов (П₁—П_i, i = = 1, . . . , п): последовательное соединение простых операций (рис. 86, а), сходящаяся (смесительная) структура (рис. 86, б), расходящаяся (разделительная) структура (рис. 86, в), сложная структура с рециклом (рис. 86, г).

Кроме технологических операций, непосредственно связанных с преобразованием свойств продуктов, производственный процесс включает транспортировку, загрузку и выгрузку, ориентацию,

перекладку и т. д., которые относят к операциям манипулирования.

Деревообрабатывающее предприятие — это сложный произ­водственный комплекс, обеспечивающий функционирование всех элементов производственного процесса. Различают две типовые структуры деревообрабатывающих предприятий.

Первая (рис. 87) характеризует предприятия (производства), конечной продукцией которых являются штучные изделия или полуфабрикаты (мебельное, тарное, столярно-строительное и лесо­пильное производства).

Вторая — структура предприятия с непрерывно-дискретным характером производства, где продукция штучная, а процессы не­прерывные (производство древесностружечных, древесноволокни­стых плит) (рис. 88).

Каждая из представленных структур позволяет судить об ос­новных материальных потоках и потоках информации, используе­мых для управления.

Используя структурное представление производств, рассмот­рим главные производства деревообработки и математическое опи­сание их основных технологических операций.

„ § 46. СТРУКТУРЫ ГЛАВНЫХ ПРОИЗВОДСТВ

ДЕРЕВООБРАБОТКИ

Лесопильное производство. В лесопильном производстве в за­висимости от способа выполнения основной операции (продоль­ного раскроя бревен) различают два вида поточных технологиче­ских линий: рамные потоки и линии агрегатной переработки бре­вен [16, 18]. Лесопильный поток можно разделить по следующим группам операций [18, 33]:

1) подготовка сырья (бревен к распиловке); 2) распиловка бре­вен; 3) механическая обработка пиломатериалов; 4) гидротермиче­ская обработка пиломатериалов; 5) погрузочно-разгрузочные пе-реместительные операции; 6) учет пиломатериалов при отгрузке.

Укрупненная структура лесопильного производства представ­лена на рис. 89, а. Лесопильное производство следует рассматри­вать как сложную систему, выпускающую установленный набор сортиментов пиломатериалов с максимальным количеством при минимуме затрат.

Фаза I лесопильного производства содержит операции: подачу бревен к гидролоткам, сброс бревен в гидролоток, подачу бревен в бассейн окорочной станции, подачу бревен к окорочным станкам, окорку бревен, подачу бревен в бассейн лесопильного цеха и их подсортировку.

Фаза II включает операции: подачу бревен к лесопильным ра­мам, пиление бревен на рамах первого и второго рядов. Фаза III представляет процессы механической обработки пиломатериалов— обрезку, торцовку досок, сортировку, пакетирование.

Следующим этапом IV является гидротермическая обработка — сушка в сушильных камерах, торцовка, маркировка. Фаза V —

лов мощности электропривода и выражается целевой функцией

погрузка готовых пиломатериалов в подвижный состав и транс­портировка на биржу, где после разгрузки их укладывают в шта­беля.

Заключительная фаза VI лесопильного производства — учет пиломатериалов и отгрузка их потребителю. При этом необходимо учитывать транспортные операции на бирже, которые имеют боль­шой удельный вес в производстве.

Качество пиломатериалов зависит от качества подготовки сырья (операций гидротермообработки и окорки), выполнения основных раскройных операций и механической обработки пиломатериалов.

Укрупненная структура лесопильного производства с рамными потоками характеризует производство как сложную систему, ко­торая должна выпускать установленный набор сортиментов пило­материалов максимального качества при минимальных затратах.

Задача управления распиловкой бревен [18] состоит в необходимости изменять посылку и периодически настраи­вать лесопильные рамы для обеспечения максимальной произво­дительности при ограничении по качеству обработки пиломатериа-

ограничения

b = f( , t) [b], [ ], (36)

где П — погонная производительность; Т — период работы пил; [b]—допустимая граница показателя точности; [ ]—допусти­мая посылка по шероховатости или мощности привода; t — время.

Качество распиловки влияет на производительность, так как рассеяние размеров пиломатериалов по толщине в пределах до­пуска обеспечивается изменением значения посылки. Максималь­ной производительности рамного потока можно достигнуть, если бревна подсортировывать по однородным потокам.

Целевая функция модели распределения сырья с учетом раз­мерно-качественной группы i, рамного потока j и постава k запи­шется как

При определении максимума производительности (35) по целе­вой функции модели (37) следует учитывать действующие ограни­чения (36) по фонду машинного времени А, по плановым объемам распиливаемого сырья определенных поставов.

Выражение (37) и имеющиеся математические модели по оп­тимальному раскрою и управлению точностью рамной распиловки позволяют сделать вывод о подготовленности лесопильного произ­водства к автоматизации управления по моделям с применением ЭВМ. Выбор технических средств, реализующих систему управле­ния, производят на основании сравнения различных вариантов, подсчитанных на основании экономико-математических моделей.

Построение автоматизированной системы управления лесопиль­ным производством, механизация операций позволяют повысить уровень организации производства, оптимизировать раскрой и обес­печить повышение производительности труда.

В последние годы широко внедряют агрегатную обра­ботку древесины, которая предполагает одновременное формиро­вание бруса и щепы.

Агрегатное оборудование предназначено для обработки бревен нормальных диаметров и тонкомерной древесины. Распиловка бруса позволяет получать 4—12 типоразмеров пиломатериалов.

Математические модели лесопильного производ­ства при агрегатной переработке бревен описывает уравнение

V_{д. c} = V_{п. с} — V_{б. п},

где V_{д. c} — объем сухих неторцованных досок; V_{п. с} — объем сырых неторцованных пиломатериалов; V_{б. п} — объем безвозвратных потерь.

пил у верхнего края бревна ( _в) и посередине бревна ( _ср) от высоты пропила H_Ср, косвенно определяющую мощность резания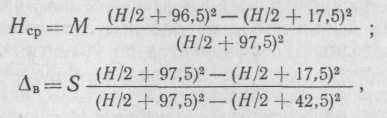

При V_{б. п} = V_{п. с} /10.

Полуфабрикаты для выработки сухой щепы оцениваются урав­нением

V _с.._щ= V (0,973 V_{п. с} + V_оп),

где V — объем круглых лесоматериалов; V_оп — объем опилок.

Объем кондиционной щепы определяют по выражению:

V_{k. щ} = 0,9 (V— V_оп)—0,8838 V_{п. с}

Рассмотренные уравнения являются основой частных матема­тических моделей для определения V_{п. с} и V_оп.

Определенные величины V_{п. с} и V_оп с поправкой на ширину досок позволяют прогнозировать выход пилопродукции для ос­новных агрегатных потоков.

Усредненная зависимость [18], выражающая математическую модель лесопильного производства при агрегатной переработке бревен, определяется уравнением:

V_п=— 0,032x²+ 0,44x + V₂₄ при x = d—24, (38)

где V₂₄ — выход пиломатериалов из бревна диаметром 24 см.

Зависимость (38) справедлива при переработке бревен диамет­ром 18<d<24 см и имеет явно выраженный экстремум.

Таким образом, на базе математических моделей агрегатной переработки древесины могут создаваться системы управления процессом, обеспечивающие заданные технико-экономические по­казатели, и выполняется моделирование данных процессов.

При агрегатной обработке древесины применяют линии агре­гатной переработки бревен (ЛАПБ), перерабатывающие бревна на пиломатериалы и щепу за один проход. Производительность ЛАПБ определяется качеством обработки, пропускной способностью аг­регата и величиной психологической загрузки оператора.

Задача управления линиями агрегатной переработки состоит в обеспечении заданной производительности при высоком качестве бруса и досок. На ЛАПБ это достигается изменением скорости по­дачи, поднастройкой фрезерных головок.

Управление линиями агрегатной переработки бревен на пило­материалы и щепу может быть принято за основу автоматизирован­ных способов управления с заданным технико-экономическим эф­фектом.

На деревообрабатывающих предприятиях изготавливают ме­бель, используя шпон ценных пород деревьев (бук, граб, красное дерево). Кряжи этих деревьев, имеющих диаметр от 0,8 до 1,8 м, распиливают на ленточнопильных станках. При больших скоро­стях подачи и ручном управлении не удается полностью использо­вать мощности станка и имеет место значительное количество брака. Брак в основном определяется недостаточной устойчивостью пилы, т. е. отклонением ее от прямой линии в поперечном направлении, что вызывает отклонение толщины отпиливаемых досок.

Исследования, выполненные в [18], позволяют записать ма­тематическую модель, характеризующую зависимость отклонения

где М — допустимое отклонение пилы посередине между направ­ляющими; S — отклонения пилы у верхнего края бревна.

Автоматическое регулирование скорости подачи в функции мощ­ности резания позволяет вести процесс на оптимальных скоростях подачи, а регулирование скорости подачи в зависимости от откло­нения пильной ленты обеспечивает высокое качество пиломатериа­лов.

Идентификация основных технологических процессов лесопиль­ного производства обеспечивает возможность оптимизации режи­мов процесса и создает условия для разработки и внедрения АСУ ТП.

Тарное производство. Низкокачественная древесина образует в лесопильном производстве свой поток — производство тары.

Малоценная древесина в основном концентрируется на лесо­заготовительных предприятиях, где и организуют тарное произ­водство. Для изготовлениятары используют хвойные породы IV и лиственные III сортов. Фазы тарного производства представлены на рис. 89, б.

На фазе I идут подготовка сырья, подсортировка, подача к ле­сопильной раме механизированным способом. На фазе II продольно раскраивают бревна в развал, отделяют фаутную сердцевинную часть от кондиционных необрезных досок и подают на дальнейшую обработку. На фазе III используют круглопильные станки, на которых раскраивают сердцевинный брус, отделяют гниль, тор­цуют годную часть бруса.

В фазе VI на ленточных станках выпиливают, торцуют и при­резают тарные заготовки. Фаза V имеет лесопильную раму РТ-2, где выпиливают тарные доски, которые далее торцуют. После при­резки на фазе VI формируют ящичные щиты на полуавтоматиче­ской линии ЭЩН. Фаза VII — заключительная, здесь собирают тарные комплекты.

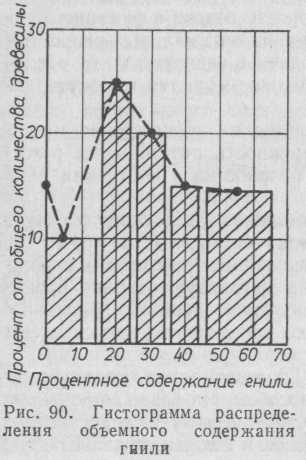
В тарном производстве есть вспомогательные производства по переработке отходов на щепу. Возможны потоки, связанные с теп­ловой обработкой заготовок и механизированные участки упа­ковки продукции. Размерно-качественная характеристика сырья данных потоков существенно влияет на эффективность перера­ботки древесины. Качественные характеристики сырья оцени­ваются гистограммами (рис. 90) и уравнением v_гн = ad², где d — распространение гнили в процентах диаметра круглых лесоматериалов; а — коэффициент, равный 1; v_гн — процентное содержание гнили в дровяной древесине. Распределение гнили в

дровяной древесине по гистограмме приблизительно 50 %, что определяет выход.

При использовании горбылей и реек для изготовления тарных заготовок объем сырья [18], м³ плотной древесины, вычисляют с помощью переводных коэффициентов по уравнениям:

V_р.пл. =kV_скл; V_г.. _пл = 0,67LBH,

где V_р.пл. — объем, м³ плотной древесины; V_скл — объем в складоч­ных единицах; k = 0,5—0,6 — переводной коэффициент для реек;

V_г.. _пл —объем горбыля, м³ плот­ной древесины; L — длина заго­товок; В — ширина пропильной части; H— средняя толщина торца; Н = (H_mах—H_min)/2.

Норму расхода березового сырья для получения короткомер-ных заготовок определяют по формуле N = V/ k, где V — объем древесины в единицах изделия (заготовок); k — коэффициент вы­хода заготовок.

Обобщенный коэффициент вы­хода заготовок

где коэффициенты: k₀— потерь древесины в опилки, k₀ = k_ш k_т (k_ш k_т — потерь в опилки по ши­рине и толщине заготовок); k_y —•■ потерь от усушки; k_L — учитывает использование кряжа по длине; k_s — выход заготовок по поперечному сечению кряжа.

Таким образом, рассмотренные зависимости определяют потреб­ное сырье или количество заготовок для производства тары, которое можно получить из поступающего сырья.

Объединение математического описания потребности сырья, модели оптимального раскроя и модели агрегатов дает систему ма­тематических уравнений, позволяющих моделировать тарное про­изводство и строить оптимальные потоки, режимы или системы управления.

Фанерное производство. Оно представляет дискретный способ производства. Технологический процесс можно разделить на три фазы: подготовка сырья к лущению, изготовление шпона, изготов­ление фанеры. Фазы производства объединяют участки: складиро­вания и подготовки сырья к лущению, лущения шпона, сушки, ребросклеивания, склеивания шпона, обрезки, шлифования. Участки разделены промежуточными запасами полуфабрикатов. Первая операция при подготовке сырья к лущению — термо­обработка в пропарочных бассейнах. Особенности автоматизации

гидротермических процессов рассмотрены в главе 14. Процессы механической обработки, транспортные операции при условии их модернизации сравнительно легко автоматизировать, используя ло­гические системы алгоритмов, основанные на законах булевой алгебры.

При технической реализации систем управления применяют контактную или бесконтактную аппаратуру (магнитные пускатели, реле, логические элементы) дискретного действия. Участок луще­ния может быть полностью автоматизирован, при условии автома­тической подачи сырья к лущильным станкам.

Существуют измерительные системы учета фанерного сырья [18], которые позволяют получить информацию о сырье, посту­пающем на обработку, в том числе и к лущильным станкам.

Определение среднего объема партии, поступаю­щей на переработку древесины в шпон, возможно при допущении, что чураки имеют одинаковую длину и вид правильных геометри­ческих тел (усеченных конусов). Доказано, что распределение кря­жей и чураков на нерассортированных поддонах подчинено лога­рифмическому закону, а время поступления на обработку или время обслуживания определяется законами теории массового обслуживания (формула Эрланга).

При табличном объеме v _i = v_cp уравнение для определения объема одного чурака будет

Объем партии, м³, рассчитывается из уравнения:

при малых величинах ²(D) получаем

Средний диаметр, м, можно определить неравенством П. Л. Чебы-шева:

При различных длинах чураков объем единичного чурака М (v_i) определяется по некоторой выборке N₀ штук и средний объем партии будет:

Представительность выборки определяется по неравенству П. Л. Чебышева:

Из (39) определяется

где М — математическое ожидание; v — объем единичного чу-рака; ² — среднее квадрэтическое отклонение.

Температура, 0С 10 20 30 40 50 60 Коэффициент at 1,1 1 0,9 0,8 0,7 0,6 Время работы после заточки, ч .... 1 2 3 4 5 6 Коэффициент а3 —1,1 1,15 1,2 1,23 1,3 1,35

Уравнения содержат информацию о диаметрах D, поэтому устанавливается точность измерения объемов по минимуму гра­даций:

где V_t — табличный действительный объем партии; V_Tmin — до­пустимая относительная погрешность измерения объема.

Лущение — основная операция для получения шпона тре­буемого размера и качества. Процесс лущения состоит из двух опе­раций: оцилиндровки чурака и получения шпона.

Операцию лущения можно автоматизировать: если автомати­зирован процесс перехода с оцилиндровки чурака на лущение. Существует несколько вариантов автоматизации такого перехода: метод статистических коэффициентов, метод контроля ленты шпона и метод контроля мощности главного электропривода станка.

Метод статистических коэффициентов позво­ляет рассчитать диаметр окружности, описываемый выступающей частью чурака при механизированной центровке, если известен диаметр в верхнем отрезе: D = D_Bk_ф (40),

где D — диаметр окружности, описываемой выступающей частью чурака; D_B — диаметр чурака в верхнем отрезке; k$ — коэффи­циент формы чурака.

Вычислить коэффициент окорки можно при помощи уравнения

Используя зависимость (40), определяют величину пути, до которой можно оцилиндровывать чурак: l = (D—D_0K)/2, после чего переходят к получению шпона. Переход можно выполнять на основании контроля качества ленты шпона (ее непрерывности), или контроля потребляемой мощности главным электродвигателем лущильного станка. Таким образом, переход от процесса оцилин­дровки к процессу лущения требует системы датчиков, обеспечи­вающих требуемую информацию и надежных исполнительных устройств.

Для процесса лущения характерно изменение диаметра чурака. Операция лущения может быть оценена с позиций формализован­ной операции, когда оценивают производительность одного станка и его участие в выполнении календарного плана производства. Р_л определяются суммарной мощностью лущения:

P_л = (F_лv_cp)102.

Средняя скорость резания, м/с, при постоянном числе оборотов чурака

v_cp = [ (D₀—D_K)] / (2 1000 60), (41)

где F_л — касательная сила лущения, кг, F_л = F_z + F_T; F_z — сила резания; F_T — тангенциальная сила; D_o и D_K — диаметры оци-линдрованного чурака и карандаша соответственно.

Сила резания F_z = (0,2 + 0,lh) ba_na_ta₃,

где h — толщина; b — ширина шпона, мм; а_п — поправочный ко­эффициент на породу (береза — 1, бук — 1,3, дуб — 1,7, кедр — 0,8); a_t, а₃ — поправочные коэффициенты на температуру гидро-термически обработанного чурака и на затупление ножа соответст­венно.

Касательная сила трения обжимной линейки по А. Л. Бер-шадскому

F_T = 0,01 _ohb,

где _o = 10—30 — степень обжима, %.

Уравнение, характеризующее силовые факторы лущения:

Силовые характеристики могут быть определены по удельным силам лущения в Н/м² (номограмма Ивановского).

В процессе лущения изменяется диаметр чурака (41), соот­ветственно изменяется (снижается) скорость резания, что влечет снижение производительности оборудования и качества шпона. Поэтому одна из главных задач при управлении процессом луще­ния — сохранение скорости резания постоянной, т. е. обеспечение регулирования скорости в функции диаметра чурака.

Процессы сушки шпона в конвейерных сушилках и термообра­ботка при прессовании фанеры рассмотрены в главе 14.

Математическое описание основных технологических процессов, анализ работы технологического и вспомогательного оборудования позволяют определить информационные потоки в фанерном произ­водстве для автоматизированного учета, контроля и управления. Знание целей производства и наличие систематизированной ин- формации о процессе дают возможность внедрять АСУ ТП на фа­нерных заводах и цехах.

Производство древесностружечных плит. Основным конструк­ционным материалом при производстве столярно-строительных изделий и мебели являются древесностружечные плиты (ДСтП). Производство этих плит представляет собой непрерывный поток сырья и дискретные изделия. Технологический процесс объединен поточной линией, содержащей около 300 единиц оборудования и промежуточных емкостей, синхронизирующих их работу. Весь процесс укрупненно можно разбить на следующие фазы (см. рис. 89, в).

В процессе производства идет подготовка стружки для наруж­ного — фаза 1а и внутреннего фаза 1б слоев с последующей суш­кой — фазы IIа, IIб. После сушки стружка проклеивается смолой — фазы (IVa) и (IVб) и поступает в машину, формирующую древес­ный ковер,— фаза V, который поступает в пресс — фаза VI и после обработки в нем проходит калибровку и сортировку фаза VII. Подготовка смол характеризуется фазой III. Все фазы разделены емкостями, позволяющими синхронизировать процесс.

Технологические основы автоматизации производства древесно­стружечных плит наиболее полно изложены в работе [4]. Мате-

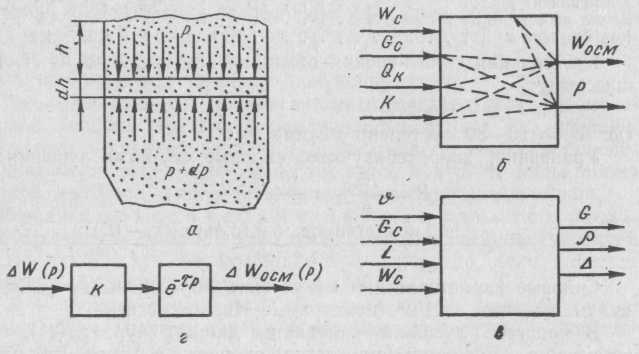
Рис. 91. Модели объектов производства ДСтП:

а — бункера со стружкой; б — процесса смешивания стружки со смолой; в — формиро­вания древесностружечного ковра; г — усилительное звено и звено запаздывания

матические модели технологических стадий в полном объеме пред­ставить затруднительно из-за их недостаточно полной разработки, поэтому рассмотрим математические модели основных процессов. На первой стадии производства, включающей поперечную распи­ловку кряжей на многопильных станках, получение стружки на стружечных станках, создание запаса сырой стружки в бункерах и ее измельчение в молотковых дробилках, функции управления состоят в учете сырья и формировании необходимых запасов и доз стружки. При известных размерах промежуточных емкостей тре­буемую величину запаса можно характеризовать уровнем стружки в емкости.

Математическая модель бункера со стружкой [18] может быть представлена уровнем стружки в зависимости от давления на боковые стенки бункера (рис. 91, а).

Уравнение материального баланса определится уравнением

F_p + F_т - F_M = 0, (42)

где F_p — сила реакции на приращение давления от увеличения глубины; F_т — сила сопротивления, обусловленная трением от

движения стружки при открытии нижнего отверстия; F_M — сила, обусловленная массой стружки.

Обозначив промежуточную площадь бункера S, периметр се­чения Р, текущий уровень h и его изменение dh, перепишем урав­нение (42):

Обозначив ( kP)/S = , получим

где k —_; коэффициент пропорциональности; р — объемная плотность стружки; — коэффициент трения стружки о боковую поверх­ность.

Постоянная интегрирования С = р. Общее решение уравнения примет вид:

Решив (44) относительно Р, получим:

Боковое давление Р_бок = kP. Тогда:

Общее решение уравнения (43) имеет вид:

Уравнение (45) устанавливает зависимость давления на стенки бункера от уровня стружки, что позволяет получить информацию о количестве стружки в промежуточных емкостях. Получение высококачественных плит возможно при стабильной влажности стружки, заданной технологическим режимом. Влажность посту­пающей стружки колеблется в широком диапазоне от 5—10 % (от­ходы мебельного производства) до 120—150 % (сплавная древе­сина), поэтому необходима сушка. Для сушки стружки в цехах древесностружечного производства применяют барабанные су­шилки, которые рассмотрены в главе 14.

Математическое описание процесса сме­шивания стружки со смолой. Процесс протекает в смесителях и качество смешения характеризуется нормой рас-хода связующего Q₀

р= 100%

и влажностью стружечно-клеевой массы W. Структурная схема модели процесса представлена на рис. 91, б.

Математическое описание [4, 18] зависимости выходных пара­метров определяется уравнениями: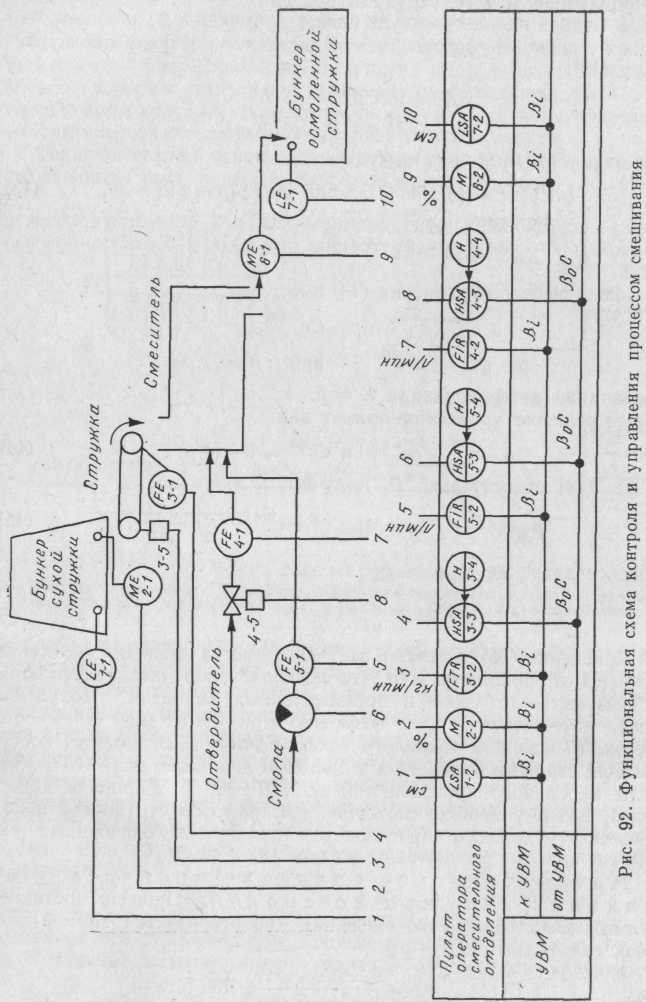

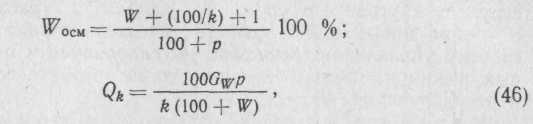
где W_ocm — влажность осмоленной стружки, %; W — влажность сухой стружки, %; р — норма расхода связующего, %; G_o — вес абсолютно сухой стружки; кг; Q_k — расход связующего с кон­центрацией k, л; G_W — расход стружки с влажностью W, кг. Расход связующего определится из уравнения (46)

Динамические свойства [18] смесителя по каналу «влажность стружки W — конечная влажность W_ocm приближенно соответст­вуют усилительному звену, последовательно включенному с зве­ном запаздывания (рис. 91, г) и выражаются передаточной функ­цией

где k = 1,8 2; = 10 20.

Передаточная функция по каналу «расход связующего — влаж­ность осмоленной стружки»

Кафедрой автоматизации производственных процессов БТИ им. С. М. Кирова по результатам исследований получены матема­тические зависимости, характеризующие процесс осмоления:

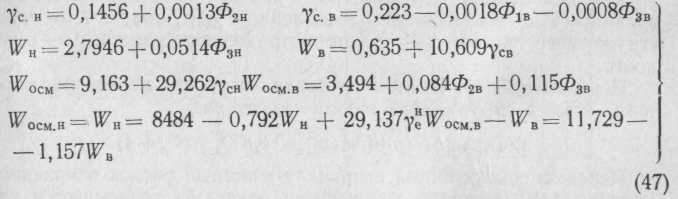
Данные регрессионного уравнения (47) характеризуют зависимость показателей процесса осмоления от некоторых параметров стружки. Здесь _сн, _св — насыпной вес сухой стружки наружного и внут­реннего слоев, %; W_н, W_в — влажность сухой стружки наружного и внутреннего слоев, %; W_{Осм. н}, W_{осм. в} —влажность осмоленной стружки по слоям, %; Ф_1Н, Ф_2Н, Ф_3Н —доли фракций 1/0,5,

0,5/0,5, 0,25/0 по весу в потоке стружки наружного слоя, %; Ф_1в, Ф_2в, Ф_3в — Доли фракций /3, 3/1, 1/0,5 по весу в потоке стружки внутреннего слоя, %. Используя уравнения (44—47), с учетом динамических свойств смесителя строят рациональную систему управления, возможно моделирование и поиск оптималь­ных режимов. Функциональная схема автоматического контроля и регулирования представлена на рис. 92.

Математическая модель формирования

древесностружечного ковра. Четкая работа фор­мирующих машин в значительной степени определяет качество готовых плит, поскольку колебания веса стружечного пакета ве­дут к неодинаковым условиям их прессования, к получению плит различной толщины, а следовательно, к различным показателям качества готовых плит. Дозирование применяют объемное или с ис­пользованием порционных весов.

Исследованиями УкрНИИМОД определена статическая модель процесса формирования древесностружечного ковра в виде рег­рессионного уравнения

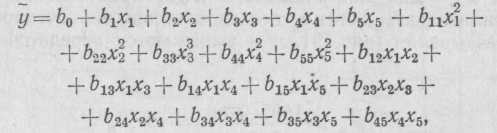
где у — среднее арифметическое коэффициента вариации плоского веса ковра; b_i b_ii, b_ij — коэффициенты регрессии, отражающие линейные, квадратичные, парные эффекты взаимодействий (i = 1, 2, . . . , 4; j = 2, . . . , 5); x₁ — положение валика питателя; х₂ — расход проклеенной стружки; х₃ — скорость конвейера питателя; х₄ — положение валика дозатора; х₅ — величина навески весов.

Динамическую модель процесса формирования древесностружеч­ного ковра можно представить в виде структурной схемы (см. рис. 91, в), где v — скорость конвейера питателя; G — массный расход осмоленной стружки; L — положение разравнивающего валика; W_Ocm — влажность осмоленной стружки; G_c — масса стружечного пакета; — толщина стружечного пакета; р — плот­ность.

Передаточная функция по каналу «скорость конвейера пита­теля — масса стружечного пакета» имеет вид

Передаточная функция по каналу «массный расход осмоленной стружки G — толщина стружечного пакета » записывается как

где k₁ k₂ — коэффициенты, зависящие от конструктивных данных объектов.

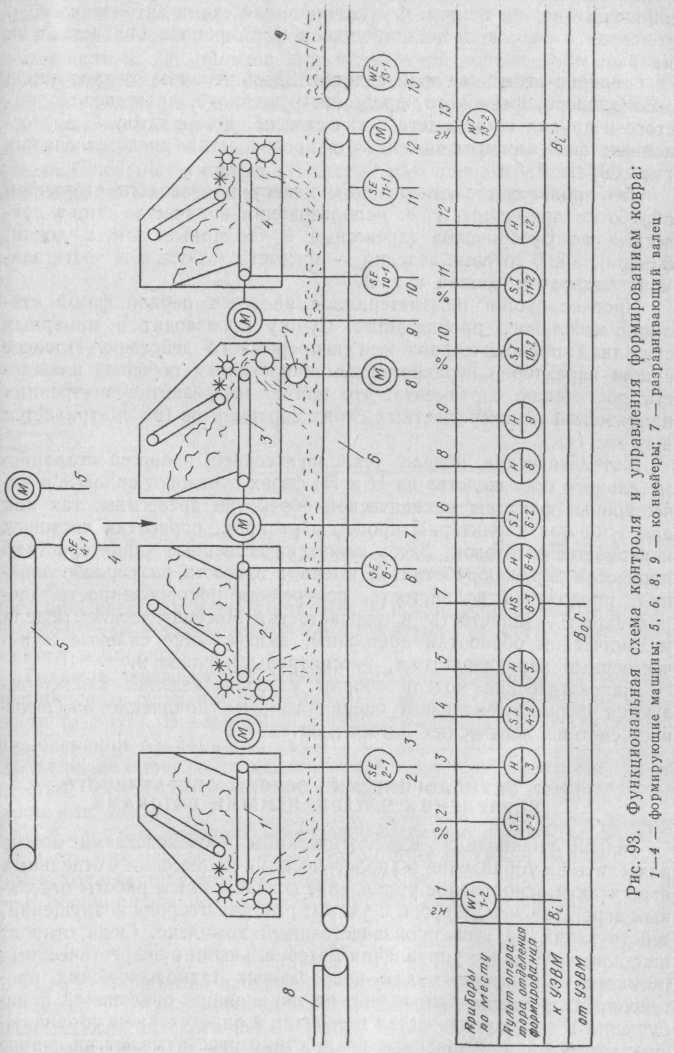
Исследование условий работы формирующих машин позволяет сформировать рациональные режимы и управление процессом на-

сыпки древесных ковров в условиях многочисленных факторов, влияющих на вес пакета. Функциональная схема автоматического контроля и регулирования процессом формирования представлена на рис. 93.

Столярно-мебельное производство. Здесь используют продукцию лесопильного, фанерного, древесностружечного, древесноволокни­стого и других производств в качестве полуфабрикатов. Схема ос­новных фаз столярно-мебельного производства представлена на рис. 89, г.

Это производство относится к классу производств вторичной обработки древесины, т. е. использования в качестве сырья дре­весных полуфабрикатов (древесные и столярные плиты, доски, фанера), а его готовые изделия — предметы мебели или части зда­ний, аппаратов, машин и т. д.

Процесс сушки пиломатериалов является первой фазой сто­лярно-мебельного производства. Сушку производят в камерных сушилках периодического или непрерывного действия. Процесс сушки характерен неравномерным нарастанием перепада влажно­сти по сечению сортимента, что влияет на развитие внутренних напряжений в поверхностных слоях сортиментов (рассматривается в главе 14).

Математические модели технологического процесса столярно-мебельного производства на II и III фазах отражают силовые и ка­чественные факторы механической обработки древесины, так как для этих фаз характерны процессы раскроя, обработки чистовых и черновых заготовок. Здесь важны качественные характеристики процессов деревообработки, а именно: точность размерообразова-ния, продольная волнистость, поперечная покоробленность, ше­роховатость, мшистость и ворсистость. Математические модели механической обработки древесины, включающие силовые и ка­чественные характеристики, рассмотрены в главе 9.

Математические модели сборки узлов и изделия характери­зуются формализованными операциями, и управление обеспечи­вает система логических алгоритмов.

S 47. ТЕХНОЛОГИЧЕСКИЕ ОСНОВЫ ОПЕРАТИВНОГО УПРАВЛЕНИЯ МАТЕРИАЛЬНЫМИ ПОТОКАМИ

Задачи управления технологическими производствами можно разделить на управление технологическими процессами в отдельных агрегатах и оперативное управление согласованием работы отдель­ных агрегатов между собой с учетом различного рода возмущений, действующих на весь производственный комплекс. Сюда относят широкий круг задач управления материальными и энергетическими потоками, характерных для непрерывных технологических про­цессов. Их решение направлено на ликвидацию отклонений и на­рушений в ходе производства и связано с определением управляю­щих воздействий. Указанные воздействия рассчитывают на основе моделей управления непрерывными технологическими процессами.

Решение может иметь два варианта. В первом случае задача решается для всей модели комплекса в целом. В реальных усло­виях при таком подходе необходимо рассматривать задачи большой размерности и, как правило, при нелинейной модели общего вида. Для построения и корректировки модели требуется обработка большого объема информации, затруднено использование моделей и алгоритмов для других задач.

Во втором случае исходная модель комплекса разбивается на модели отдельных типовых процессов или операций преобразова­ния потоков. Размерность уменьшается, и даже в случае нелиней-

ного описания ее удается достаточно успешно решить. На типовых моделях определяют существенные свойства структур технологи­ческого комплекса.

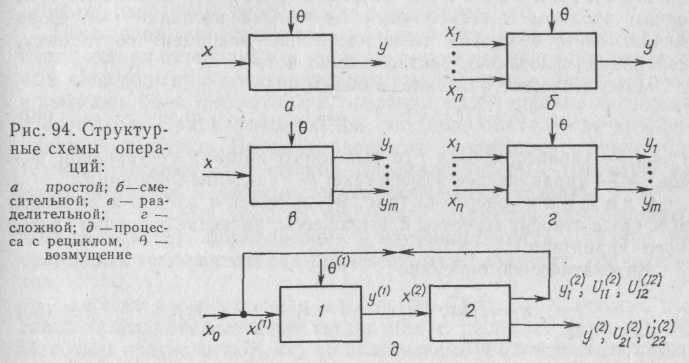
Типовые операции. Выделение типовых операций позволяет сформировать основные математические модели процессов при соз­дании АСУ ТП. В непрерывных технологических процессах типо­вые операции рационально связать с числом материальных пото­ков на входе и выходе технологической операции. Можно выделить простые, смесительные, разделительные, сложные типовые про­цессы или операции.

Простая операция имеет один выходной поток (рис. 94, а). Сюда относят модели различных процессов деревообработки с од­ним исходным продуктом и одним выходом.

В общем случае операцию можно описать зависимостью

х = f (y, V),

где х, у — параметры входного и выходного потока; f — заданная функция; V — управляющее воздействие, связанное с выполне­нием технологического регламента.

Смесительная операция имеет несколько входных (п) и один выходной поток (рис. 94, б). Этой операции соответствуют

Уравнения смесительных и разделительных операций с учетом (48) можно записать:

процессы смешения в деревообрабатывающей промышленности и других отраслях. Сюда относят смешение: стружки и связующего, проклеивающих компонентов и древесной массы при производстве ДВП, компонентов при приготовлении смол и т. д. Математическое описание в общем виде

x_i = f_i (y, V), i=l, . . . , n, (48)

где x_i, у — характеристика i-гo входного потока и общего выход­ного потока; V — управляющее воздействие, связанное с выпол­нением технологического регламента; f_i — заданная функция.

Разделительная операция (рис. 94, в) характеризуется одним входным и несколькими выходными потоками (т). Сюда можно отнести многие технологические операции: сортировку, сепарацию, флотацию, ректификацию и т. д.

Математическое описание в общем виде

y_i=f_j(x, V), j=1, . . . , т, (49)

где y_i, — характеристика j-го выходного потока; х — входной по­ток; V — управляющее воздействие; f_j;- — заданная функция.

Сложная операция (рис. 94, г) имеет п входов и т выхо­дов. Сюда относят агрегаты или процессы, имеющие операции слож­ного характера.

Математическое описание

y_i = f_j ( , ), j =1, . . ., т, (50)

где и — векторы.

Модели рассмотренных операций, имеющих линейный харак­тер (48) — (50), легко изучать, моделировать, анализ и расчет мо­делей технологических комплексов, как правило, осложнены только размерностью модели. Наибольший интерес представляют линей­ные модели технологических процессов с переменными коэффици­ентами. Математическое описание таких моделей можно предста­вить уравнением

где f_ji — заданные функции от V.

Модель линейна и управление потоком может производиться изменением либо x_i, либо коэффициента f_ji.

Коэффициент f_ji, определяемый свойствами рассматриваемой операции и требованиями технологии, может быть ограничен v .

В общем случае модель можно линеаризовать по входным по­токам x_j путем разложения f_j ( , х) в ряд Тейлора в окрестности некоторого значения входных параметров х₀.

Введем новые переменные и_ji = f_ji (V). Тогда

На показатели качества выходного потока положены ограниче­ния. Следовательно, уравнение (51) справедливо при и U. Проа­нализировав приведенные модели, их можно отнести к классу ли­нейных уравнений с переменными коэффициентами.

Переменные коэффициенты характеризуют количественные ха­рактеристики материальных потоков. В простой операции перемен­ный коэффициент характеризует затраты сырья на единицу готовой продукции. Для смесительной операции коэффициенты являются расходными. При разделительной операции они служат коэффи­циентами выпуска. Во всех процессах коэффициенты являются технологическими параметрами. Линейные модели с переменными коэффициентами — частные случаи нелинейных моделей.

Знание типовых моделей отдельных процессов или операций дает возможность формализации и изучения свойств структур не­прерывных технологических процессов, охватывающих ряд агрега­тов.

Наиболее распространены последовательное, параллельное, по­следовательно-параллельное соединения с рециклом (рис. 94, д). При этом предполагают, что количественные и качественные пока­затели материальных потоков не изменяются на участке перехода от одной операции к другой.

Используя модели отдельных процессов, можно рассматривать, изучать и решать задачи управления непрерывными технологиче­скими процессами в условиях функционирования АСУ ТП.

Управляющие воздействия определяют исходя из выполнения заданных критериев, ограничений на количественные и качествен­ные параметры входных и выходных материальных потоков.

Критериями для технологических комплексов с непрерывными технологическими процессами могут быть: прибыль, производи­тельность, объем выпускаемой продукции, затраты на функциони­рование установок и др. Наиболее часто используются критерии производительности и прибыли (себестоимости).

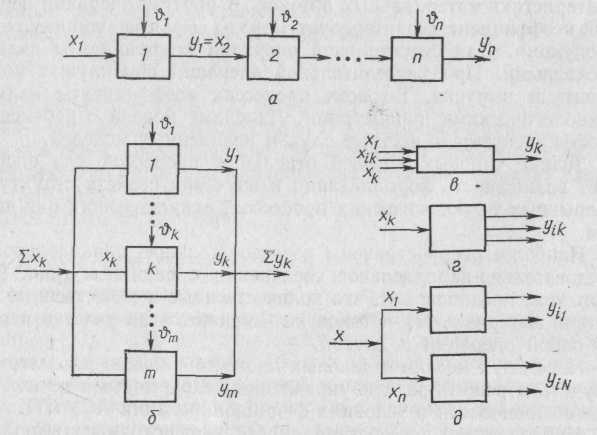
Алгоритмы оперативного управления. Рассмотрим определение алгоритмов управления, моделирования простых непрерывных про­цессов или операций при последовательном, параллельном и по­следовательно-параллельном соединении.

Алгоритм управления при последовательном соединении п про­стых операций x_k = v_ky_k (рис. 95, а) характеризуется условием последовательности

и ограничением

0 x_k x^,,_k; k= 1, . . . , п,

где x^,,_k — заданные числа.

Задача максимизации производительности у_п max заклю­чается в выборе значений x_k и v_k, при которых удовлетворяются ограничения.

На основании (51) и (52) запишем задачу максимизации произ­водительности:

Если заменить переменные x_k = v_ky_k, то задачу (54) сводят к эк­вивалентной задаче линейного программирования:

Рис. 95. Схемы соединения операций: а—д — варианты алгоритмов

Сформулированная задача запишется в виде

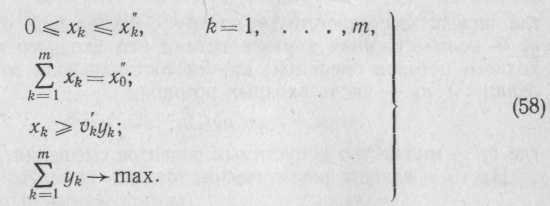
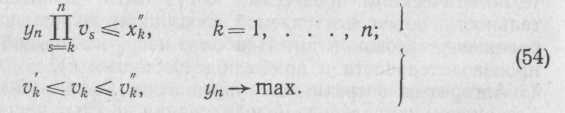
Так как в (53) есть произведение переменных, задача (54) от­носится к классу задач нелинейного программирования и допускает простую процедуру решения.

Оптимальное значение потока на выходе комплекса определится

формулой

Если максимальное значение у_{п. опт} достигается при k = 1, то l-я простая операция является «узким местом» технологического непрерывного потока, так как она лимитирует прохождение потока по всей последовательной цепи операций и определяет конечную производительность и оптимальное значение функционала у_п.

Если ввести в задачу (54) ограничения на план выпуска

у_п = х_п+1 у’_п (55)

и в качестве функционала принять затраты производства, можно сформировать линейную задачу минимизации затрат

где С_k —себестоимость переработки сырья на k-й операции.

Алгоритм управления при параллельном соедине­нии т простых операций x_k = v_ky_k (рис. 95, б) характерен для распределения нагрузок между параллельными агрегатами. Рас­смотрим модели с переменными коэффициентами вида x_k = v_ky_k.

Максимизация производительности при ограничении на вели-

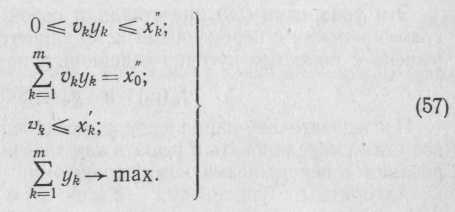
чину суммарного потока = x’’₀ по выходу может быть сформулирована в виде системы уравнений:

При решении задачи (57) определяют значения переменных x_h, y_k. Величину v_k определяют из уравнения (51).

Задача минимизации затрат при параллельном соединении т

Зависимость качественных показателей смеси от управляющих воздействий и_ik, принимаем линейной, тогда

простых операций рассматривается при ограничении производи­тельности комплекса по входу и выходу:

Таким образом, затраты на каждой операции можно записать, используя формулу G_k = q_k (v) х_k, следующим образом:

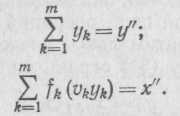
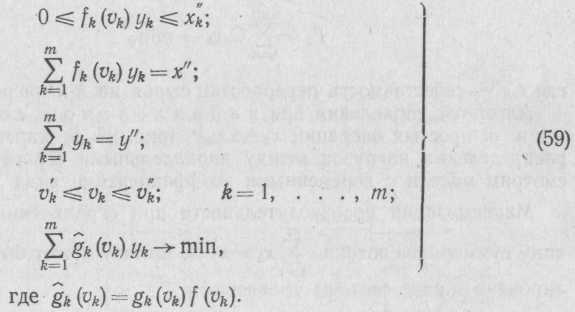
Эти уравнения (59) представляют собой задачу линейного про­граммирования с переменными коэффициентами, и она может быть решена с помощью кусочно-линейной аппроксимации функции

Последовательно-параллельное соединение простых операций возможно моделировать и решать как задачи линейного программи­рования с переменными коэффициентами.

Алгоритмы управления смесительными опера­циями. Смесительная операция характеризуется несколькими входными и одним выходным материальным потоком (рис. 95, в)

x_ik = u_iky_k, i=1, . . . , n_k,

где индекс k соответствует номеру смесительной операции; x_ik, у_k — количественная характеристика i-го входного и общего выходного потоков операции; u_i—i-я составляющая вектора управления v_k; n_k — число входных потоков.

где v_k — множество допустимых рецептов смешения. Пусть и_k заданы аналитически, тогда

u’_ik, u’’_ik — заданные вещественные числа.

где v_sk — значение s-гo качественного показателя выходного по­тока; u_sik — значение s-гo качественного показателя i-гo входного потока; m_k —- число контролируемых качественных показателей. Обычно v_sik заданы, а на значение v_sk положены ограничения

Учитывая (61), можно записать

множество v_k определяется.

Постановка задачи смешения [13] возможна, если существуют решения, удовлетворяющие ограничениям (60) — (63). В этом слу­чае решение ищется из условия критерия

F (и, y) min (max).

Если в качестве критерия рассматривать прибыль,

Сформулированную задачу управления смешения можно пред­ставить математической моделью:

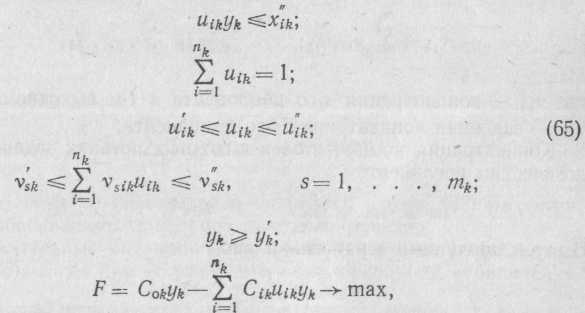
где С_оk — отпускная цена единицы смеси; С_ik — себестоимость единицы i-гo входного потока.

Эта задача (65) формально относится к классу обобщенных за­дач линейного программирования. Определяют значения парамет­ров u_ik и у_k и, используя уравнение, находят величины входных

Критерием разделения примем прибыль

потоков. Эта формулировка задачи называется формулиров­кой в относительных единицах.

Используя стандартную процедуру, можно перейти от задачи обобщенного линейного программирования к эквивалентной за­даче линейного программирования в абсолютных единицах, произ­водя замену переменных из (52).

Алгоритмы управления разделительных опера­ций. Такие операции имеют один входной и несколько выходных потоков. Эта модель достаточно широко характеризует процессы сортировки, флотации, ректификации, адсорбции и т. д. (рис.95, г).

Обычно на каждой стадии процесса смесь разделяется на два компонента.

Рассмотрим модель разделительной операции

y_ik = u_ikx_k, i=1, . . . ,m_k,

где k — индекс, отвечающий номеру операции; x_k, у_k — характе­ристики входного и i-гo выходного потока; u_k={u_ik} — вектор управляющих воздействий, связанный с распределением входных потоков; т_k — число выходных потоков, u_k u_k.

Разделительную операцию рассмотрим в случае аналитического задания множества u_k.

Рассмотрим разделение смеси, содержащей l_k компонентов. Усло­вие материального баланса по концентрации этого компонента в смеси:

где v_sk — концентрация s-гo компонента в i-м выходном потоке, _sk — заданная концентрация s-гo компонента.

Концентрация компонентов в выходных потоках задана техно­логическим регламентом

где C_ik — цена i-гo выходного продукта; С_ох — удельные затраты. Задачу оптимального разделения можно записать в следующем виде: дополняем критерий (70) ограничениями

Формулировки (70), (71), как и для смесительной операции (65),— формулировки в относительных единицах.

Перейдя к абсолютным значениям потоков y_ik, уравнения (61), (71), можно переписать:

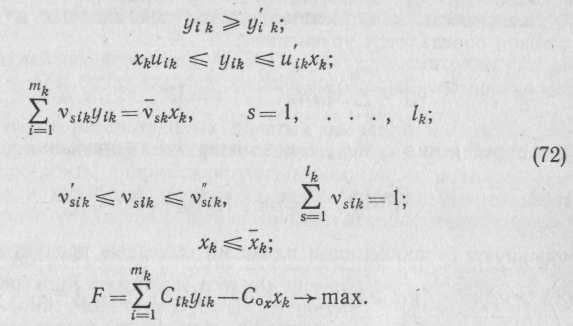
Выпуск продукции ограничен планом

Таким образом, разделение компонентов определяется ограни­чениями (66) — (69) и соотношениями для управлений и концентра­ций

По аналогии со смесительной операцией задача (72) является задачей обобщенного линейного программирования.

Разделительные операции могут быть соединены параллельно (рис. 95, д), тогда при N разделительных операциях ограничения

(72) сохраняют и вводят ограничения входного потока ;

выполнение плана у_ik y’_ik, i = 1, . . ., m_k;

величины прибыли

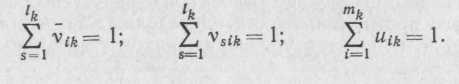
Ограничения для разделительной операции с двумя выход­ными потоками запишутся аналогично (72):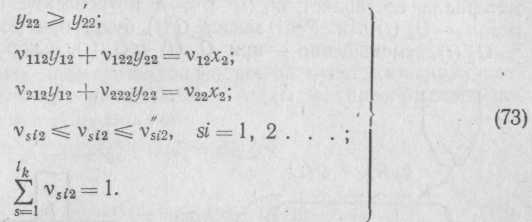

Решение является результатом применения стандартных про-цедур линейного программирования.

Алгоритмы управления последовательным соеди­нением разделительных операций (см. рис. 95, г). Операции описываются системой уравнений (51).

Последовательное соединение операций описывается как

x_k = y_g(k-1); k = 2. . . . , N, g=1.

Дополнительными ограничениями к (51) являются ограничения на качественные показатели продуктов. Качество промежуточных продуктов:

k=1, . . ., N—1;

качество готовых продуктов:

k=1, . . ., N— 1, i = 1, . . . , mk;

s= 1, . . . , l_k;

качество исходного продукта:

—заданные значения концентраций.

Зависимость качественных показателей входных и выходных потоков определится уравнением:

s= 1, . . . , l_k

Для определения x_k и y_ik, максимизирующих прибыль

дополняют ограничениями плана на выходные продукты:

k=1, . . . , N, i = 2, . . . , т_k

и запасы исходного продукта х₁ .

Задача при последовательном соединении разделительных опе­раций может быть сведена к эквивалентной задаче линейного про­граммирования путем замены переменных.

Алгоритм управления непрерывных технологи­ческих процессов по схеме с рециклом при­меняют, когда часть продукта возвращается в начало процесса (сортировка стружки при производстве ДСтП, щепы при производстве ДВП, флотация и т. д.).

Простейшая схема (см. рис. 94, д) включает простую и разде­лительную операции

Из условия материального баланса х₂ = у₁ (см. рис. 94, д) по­лучим:

х₂ = f₁(v₁)x₁=O;

x₁—x_o—y₁₂=O.

При укзанных ограничениях (73) — (74) может быть постав­лена задача максимизации прибыли

F = C₂₂y₂₂—C_oxx_o—g₁(V₁)х₁ — С₂х₂ max.

Переменные параметры x_1, х₂, х₀, y₁₂, y₂₂, v_si, V. Показатели качества v_si могут выбираться по условиям технологического рег­ламента.

При линейных функциях f₁ (V₁), g₁ (V₁) рассматриваемая за­дача (73) — (74) будет задачей обобщенного линейного программи­рования.

Применение рассмотренных простых операций и схем их сое­динения при описании сложных технологических комплексов по­зволяет построить аппроксимирующую модель, выполнить моде­лирование и имитацию процессов, найти оптимальные варианты оперативного управления непрерывными технологическими про­цессами.

В данном параграфе описана формализация непрерывных про­цессов с позиций структуры потоков для простейших технологиче­ских операций. Модели отдельных процессов, отражающих качест­венные показатели (температуру, массу, давление, частоту враще­ния, уровень, толщину и т. д.), рассмотрены в главах 8, 9, 14 как типовые модели.