§ 42. Оптимизационная математическая модель производства

Производство можно представить как набор последовательных преобразований, превращающих исходный материал в готовую продукцию. Одинаковая продукция может быть получена при раз­ных наборах преобразований и одинаковый набор преобразований может дать различную продукцию. Производство характеризуется ассортиментом и объемом. Множество B_i = {b_i0, b_i1, . . . , b_in},i = = 1, 2, . . . , k характеризует возможные состояния исходного

материала 6,- при преобразовании в готовое изделие b_in. Мно­жества b_i0 могут быть пересекающимися или непересекающимися.

Преобразование j=1,2,3 п

производится оператором a_ij. Оператором называют рабочее место, станок, робототехническое устройство, околостаночный механизм, устройства и системы автоматики, автоматизированные производст­венные комплексы, которые выполняют целенаправленные дейст­вия, связанные с преобразованием исходного материала в готовую продукцию. Набором всех операторов: существующих, создавае­мых, и тех, которые будут созданы в ближайшем будущем, является множество А А_i, А_i = {a_i1, a_i2, . . . , a_in}, i= 1, 2, . . . ,k, причем возможно равенство ряда членов а_i(j-r) = а_i(j-r+1) = а_i(j-r+2), j = 1, 2, . . . , r, . . . , п и так далее. В свою очередь каждый член j = 1, 2, . . . , п описы-

вается рядом параметров, образующих множество a_ij = {x_ij1, x_ij2, . . ,

. . . , x_ijl. Каждый параметр может иметь

фиксированное значение или изменяться в некотором диапазоне

Далее параметры могут быть независимыми

или зависеть от других параметров х_ij а_ij. Можно найти r мно­жеств А_r = {т₁ а₁,т₂ а₂, . . . т_ра_р}, где а_р А, т_р — вектор, с помощью которого обеспечивается выполнение преобразований

В_r = {q₀b₀ , q₁b₁, . . . , q_pb_p}, где — числo

преобразований, необходимых для выпуска заданного количества

изделий.

Задача оптимизации заключается в нахождении такого мно­жества А_r при котором заданное количество всех видов продукции будет изготовлено наилучшим образом. Ее решение позволяет найти оптимальный уровень автоматизации производства, состав и параметры оборудования.

Оценку вариантов А_r, (выбор оптимального варианта) произво­дят по критерию — удельные приведенные затраты на единицу продукции. В качестве условий и ограничений принимают: обеспе­чение выпуска заданного объема продукции; необходимость раз­мещения оборудования на производственной площади ограничен­ных размеров; обеспечение заданных показателей: число рабочих на участке, съем продукции с 1 м² производственной площади, удельный расход электроэнергии и др. В качестве ограничений могут выступать различные ресурсы (финансы, трудовые, энергия, сырье и материалы и др.), а также срок окупаемости и другие по­казатели.

Математическая модель оптимизации производства имеет вид:

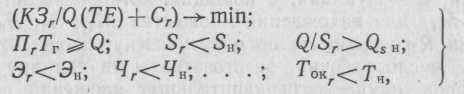
где КЗ_r — капитальные затраты на r-вариант; Q — программа предприятия; С_r — затраты на выпуск единицы продукции; ТЕ — срок окупаемости капитальных затрат; Т_г — годовой фонд рабо­чего времени; П_r S_r, Q/S_r, Э_r, Ч_r — показатели по r-му варианту: производительность, производственная площадь, съем продукции с единицы производственной площади, энергоемкость, число лю­дей соответственно; S_Н, Q_sh, Э_н, Ч_н — нормативные значения (или реальные характеристики производства): производственная пло­щадь, съем с единицы производственной площади, расход энергии, численность рабочих соответственно; T_ОКr. — срок окупаемости капитальных затрат по r-му варианту; Т_н—нормативный отрас­левой срок окупаемости.

В качестве ограничения могут быть и другие показатели и ха­рактеристики конкретных производств.

Анализируемое число вариантов может быть чрезвычайно ве­лико, что сделает расчет на ЭВМ не выполнимым. Поэтому задача решается по этапам. Производственный процесс разбивают на участки. Проводят оптимизацию в пределах участка. Находят подмножества А_п А и, упорядочивая их (вводя вектор М), на-

ходят подмножества . Из них выделяют ряд множеств А_nR, R r_n, расположенных в окрестностях оптимальных значений. При оптимизации всего производства находят множества

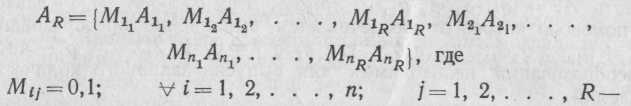
вектор, определяющий возможность получения заданного количе­ства и ассортимента продукции.

Для деревообрабатывающих производств, которые не являются фондоемкими, как показывает опыт, изменения удельных приве­денных затрат и затрат на изготовление единицы продукции имеют одинаковые закономерности [22]. Тогда оптимизационную модель можно записать в виде:

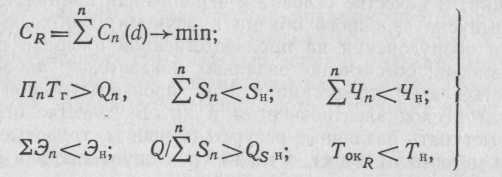
где С_n (d) — затраты на n-м участке на изготовление единицы продукции; d — функция, с помощью которой задается значение векторов М_{/ для нахождения множества M_ij; S_n, П_п, Ч_п, Э_п — показатели R-го варианта по п-му участку; площадь, производи­тельность, число рабочих, энергозатраты на единицу продукции; T_okr — срок окупаемости капитальных вложений по R-му ва­рианту.

Рассмотрим порядок оптимизации состава оборудования и его характеристик на п-м участке. Операторы, из которых может со­стоять участок, образуют множество

А_п = {а_n1, а_n2,. . . , а_nl}. Операторы а_ni,

i=l, 2, . . . , l различаются или функциональным назначением, или параметрами. Множество, определяющее состав оборудования на участке, будет

Вектор _i, = М_iт_i i=l, 2 l, где M_i = 0, 1 — вектор,

осуществляющий выбор по функциональным возможностям (М_i = = 0 — оператор отсутствует; М_i = 1 — оператор используется), т_i = 1, 2, 3 ... — вектор, определяющий число i-x операторов, необходимых для обеспечения выпуска заданного числа изделий (объема продукции). Пусть реальная фактическая производитель­ность операторов равна П₁ > П₂ > . . . > П_l. Рассмотрим случай, когда функциональное назначение всех операторов одинаково и

участок имеет одинаковое оборудование. Тогда возможно получить r = l упорядоченных множеств:

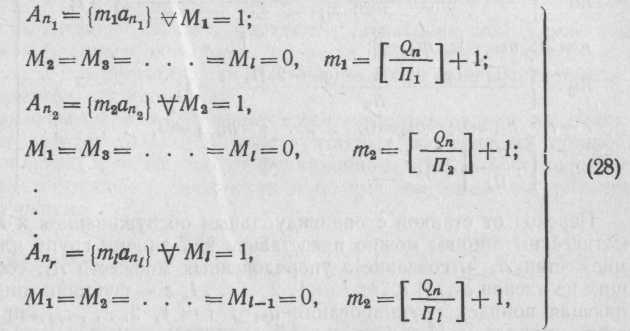
где Q_n — объем продукции на л-м участке при программе пред­приятия Q;

целая часть соответствующей дроби.

При условии, что на участке может использоваться оборудова­ние с различной производительностью, векторы m_i находят из сле­дующего:

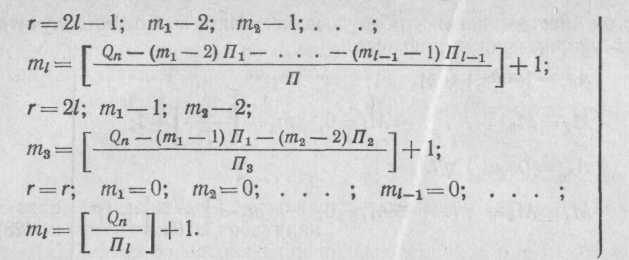
Переход от станков с индивидуальным обслуживанием к авто­матическим линиям можно представить как замену групп членов множества А_п и создание s упорядоченных множеств A_s, состоя­щих из членов z — функция, опреде­ляющая порядок группирования причем возможно a_nsj = a_пi. Определение характеристик, в том числе производительности, является самостоятельной задачей. Затем используя векторы M_sj и m_sj , которые находят по условиям (28) или (29), находят множества

Совместный анализ множеств . и позволяет решить вопрос оптимизации уровня автоматизации и состава оборудова­ния (автоматических линий) на п-м участке производства и целе­сообразности их использования. Однако оптимальный вариант на одном из участков может оказаться неудовлетворительным при оптимизации всего производства, так как объективно функцией d с оптимальным вариантом по одному участку могут сопрягаться худшие варианты по смежным участкам. Поэтому при "оптимизации участка необходимо знать данные не только для лучшего, но и для других вариантов, представляющих интерес с точки зрения" опти­мизации производства. Обычно это варианты, однозначно опреде­ляющие выбор вариантов по смежным участкам. Например, в ме­бельном производстве облицовывание плит пластиком исключает необходимость их шлифования и отделки.

Определим, из чего складываются затраты на л-м участке на изготовление продукции по r-му и r_s-мy вариантам. Для упроще­ния индексы п, r и r_s опустим. Тогда затраты на выпуск единицы продукции

где С_i —затраты, связанные с преобразованием материала в про­дукцию t-м оператором; затраты: d — функция, определяющая выбор значений i (из каких операторов состоит участок); МТ_i — на материал на единицу продукции; Э_i — на энергию на единицу продукции; И_i — на инструмент и приспособления; Р_i — на ре-

монт и техническое обслуживание; З_i — заработная плата рабочих; A_i — амортизационные отчисления на полное восстановление обо­рудования и производственных помещений.

В выражении (30) не учитываются затраты на содержание не­производственного персонала, целиком зависящие от структуры отрасли и предприятия, так как они не связаны непосредственно с предметом исследования.

Все виды затрат в (30) выражаются в денежных единицах. Часть затрат зависит только от конструктивных особенностей станков и технологии и не зависит от функционирования, т. е. от характе­ристик выпускаемой продукции и объема выпуска. Эти затраты будут равны:

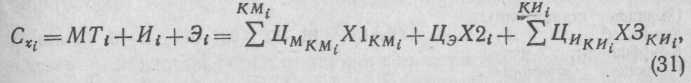
где Х1_КМi — расход материала KМi-го вида на i-м операторе (обо­рудования); X2_i — расход энергии на i-м (оборудовании) опера­торе; Х3_КИi. — расход инструмента и приспособлений КИi-го вида на i-м операторе (оборудования); Цм_КМi., Цэ, Ци_КИi.— цены еди-ницы материала КМ-гo вида, энергии, инструмента и приспособ­лений КИ-го вида (Цэ = 0,015 р/кВт ч).

В частном случае для отдельных операторов, загрузчиков или конвейеров может быть И_i = 0; МТ_i = 0; Э_i = 0. Затраты на ремонт и амортизацию зависят от времени на обработку единицы продукции и будут равны

где 3 _i. = зХ6_i— затраты на заработную плату на i-м станке; з — заработная плата одного рабочего в единицу времени (час, смену) с учетом профессии, квалификации и всех видов начислений; Х6_i — число рабочих на i-м операторе (станке); Р _i. = рХ7_i/Т_г— затраты на ремонт в единицу времени; р — затраты на ремонт оператора, имеющего ремонтную сложность равную 1 в год (по данным ВНИИДМАШ р= 80—140 р/г); X7_i — ремонтная слож­ность i-гo оператора; Т_г = 4160_r-годовой фонд рабочего времени при двухсменной работе; A _i = (H_MX8_i+Ц_sH_sS_i)/T_г — аморти­зационные отчисления на восстановление оборудования и произ­водственной площади; П_фi— фактическая производительность участка (см. § 44); H_M, H_s — норма амортизационных отчислений (H_M = 0,143; H_s = 0,100); Х8_i —стоимость i-го оператора; Ц_s= = 120—125 р.— цена 1 м² производственной площади [35]; S_i=S_ciK_si + S_ni.— производственная площадь, занимаемая i-м оператором; S_ci. = X9_{X\0_{— площадь, занимаемая соответст­вующим оператором; Х9_i; Х10_i — габаритные размеры оператора; K_si,— коэффициент, 'учитывающий дополнительную площадь на

проходы, проезды и т. д. (см. ниже); S_ni = X11_i X12_i h _i — пло­щадь под подстопные места (h = 2 — для станков и линий, обору­дованных загрузочными и разгрузочными устройствами, h = 4 — для оборудования с ручной загрузкой и разгрузкой); X11_i X12_i — габариты изделий, обрабатываемых на i-м операторе; _i — функ­ция, определяющая формирование стопы заготовок (деталей), т. е. число заготовок в стопе по длине и ширине; Q _n — плановое за­дание на выпуск продукции в единицу времени на n-м участке производства.

Ниже приведены значения коэффициента, учитывающего до­полнительную площадь на проезды и проходы в зависимости от площади оборудования:

Площадь станка или линии, м2 2—5 5—15 15—20 20—40 4 75 Свыше 75 Коэффициент, учи­ тывающий дополни­ тельную площадь, К$1 5 4 3 2,5 2 1,5

С учетом (31) и (32) имеем С’= С_х + С /П_T или С" = С_х + + С /Q_n, где П_T — техническая производительность.

Таким образом, затраты на единицу продукции зависят от по­стоянных параметров С_х и С , характеризующих данный вид обо­рудования или конкретную модель его, системы автоматики, тех­нологический процесс и объем выпускаемой продукции. Значение затрат С’ — минимальное для данного варианта участка произ­водства, а значение С" — то, которое может быть получено в ус­ловиях реального производства с объемом выпуска продукции Q_n.