§ 34. Характеристики автоматических систем управления

Совокупность устройств, подключаемых к объекту управления для автоматического регулирования его параметров, называется автоматическим регулятором. Непосредственно с объектом управ­ления связаны измерительный элемент и исполнительный механизм регулятора. Входной величиной регулятора является регулируе­мый параметр, выходной — положение регулирующего органа.

Автоматические регуляторы и законы регулирования. Автомати­ческий регулятор измеряет отклонение регулируемого параметра от заданного значения и в соответствии с реализованным законом регулирования воздействует на регулирующий орган для умень­шения этого отклонения. В промышленности для автоматизации различных технологических процессов используют множество ре­гуляторов, отличающихся друг от друга разнообразными призна­ками.

Автоматические регуляторы классифицируют по следующим наиболее характерным признакам:

по назначению — регуляторы температуры, давления и т. д.;

в зависимости от источника энергии — регуляторы прямого и непрямого действия;

по конструктивному оформлению — регуляторы приборного типа, в котором все основные элементы смонтированы в одном кор­пусе, и агрегатные, состоящие из отдельных унифицированных блоков, каждый из которых имеет определенное назначение, что дает возможность разрабатывать схемы регулирования любой сложности;

по виду используемой энергии — регуляторы электрические, пневматические, гидравлические и комбинированные.

Основной характеристикой регулятора является реализован­ный в нем закон регулирования — зависимость между изменением регулируемого параметра и положением регулируемого органа. По характеру воздействия на регулируемый орган разли­чают регуляторы непрерывного и дискретного действия.

Основными элементами регулятора являются (рис. 63):

измерительное устрoйство ИУ для измерения регулируемой ве­личины; задающее устройство ЗУ для ручного или автоматического ввода заданного значения регулируемой величины;

устройство сравнения УС измеряемого и заданного значений для определения величины и знака отклонения; управляющее устройство УУ для вычисления величины регулирующего воздейст­вия; исполнительный механизм ИМ для управления регулирую­щим органом РО на входе технологического объекта.

Регуляторы непрерывного действия в зависимости от реали­ зуемого закона регулирования подразделяются на следующие типы: интегральные — И-регуляторы; пропорциональные — П-ре- гуляторы; пропорционально-интегральные — ПИ-регуляторы;

пропорционально-интегрально-дифференциальные — ПИД-регуля-торы.

Пропорциональными, или статическими, регуляторами называют такие регуляторы, у которых положение регулирующего органа пропорционально отклонению регулируе­мого параметра от заданного значения: х = — К_ру, где К_р — ко­эффициент передачи регулятора, являющийся показателем его на­стройки.

Передаточная функция П-регулятора имеет следующий вид: W(p) = - К_р.

Преимуществом П-регулятора является его быстродействий, т. е. малое время переходного процесса и высокая устойчивость процесса регулирования. Основным недостатком П-регулятора яв­ляется наличие остаточного отклонения регулируемого параметра, что снижает точность регулирования.

Интегральными, или астатическими, на­зываются регуляторы, у которых при отклонении регулируемого параметра от заданного значения регулируемый орган переме­щается до тех пор, пока регулируемый параметр не вернется к за­данному значению. В таких регуляторах скорость перемещения ре-

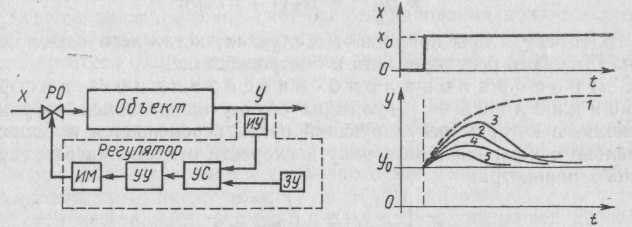
Рис. 63. Структурная схема регулятора

Рис. 64. Характеристики переходного процесса для различного типа регу­ляторов:

1 — отсутствие регулятора; 2 — П-регулятор; 3 — И-регулятор; 4 — ПИ-регулятор;

5 — ПИД-регулятор

гулирующего органа пропорциональна величине отклонения ре­гулируемого параметра от заданного значения: (dx)/(df) = — Т_иу. Проинтегрировав это выражение, получим

где T_и — постоянная времени, представляющая собой время, за которое регулирующий орган переместится из одного крайнего положения в другое при максимальном отклонении регулируемого параметра от заданного значения. Параметр T_и является показате- лем настройки И-регулятора.

И-регулятор достаточно точно поддерживает заданное значение регулируемого параметра, но процесс регулирования протекает достаточно медленно, поэтому его используют в объектах с боль­шим самовыравниванием, с незначительным запаздыванием и ма­лыми по величине отклонениями.

Пропорционально-интегральные, или изо-д р о м н ы е, регуляторы характеризуются тем, что при от­клонении регулируемой величины от заданного значения они вна­чале перемещают регулирующий орган пропорционально отклоне­нию (как П-регулятор), а затем при подходе регулируемой вели­чины к заданному значению медленно доводят ее до этого значения (как И-регулятор). Такое регулирование достаточно точно и бы­стродействующе.

Регулятор, действующий по такому принципу, называется ПИ-регулятором. Такие регуляторы действуют по следующему за­кону регулирования

где K_р — коэффициент передачи регулятора; Т_и — время изодрома; K_Р и Т_и — показатели настройки регулятора. Передаточная функ­ция ПИ-регулятора имеет вид

ПИ-регуляторы применяют в случаях, когда необходима боль­шая точность регулирования и быстродействие.

Пропорционально-интегрально - диффе­ренциальные регуляторы осуществляют закон регулиро­вания, в котором регулирующий орган перемещается пропорцио­нально отклонению, интегралу и скорости отклонения регулируе­мого параметра:

где K_Р — коэффициент передачи регулятора; T_и — время изодрома; Т_П — время предварения.

Параметры К_Р, Т_и, Т_П являются показателями настройки ПИД-регулятора. Передаточная функция такого регулятора имеет вид

ПИД-регуляторы сложнее других регуляторов в настройке, однако они могут обеспечивать более высокое динамическое ка­чество систем регулирования.

На рис. 64 для сравнения приведены характеристики П-, И, ПИ- и ПИД-регуляторов; на входе регуляторам приложено скачко­образное изменение возмущающего воздействия, объект управле­ния для всех регуляторов один и тот же. Показано, как изменяется регулируемая величина для регуляторов различного типа, а также при отсутствии регулятора. При П-регуляторе в установившемся режиме остается некоторое отклонение регулируемой величины от заданного значения, при И-регуляторе это отклонение сводится к нулю. ПИ- и ПИД-регуляторы обеспечивают лучшее динамиче­ское качество.

Регуляторы дискретного действия подразделяются на релей­ные и импульсные. В таких регуляторах регулирующий орган пе­ремещается через определенные промежутки времени. Регулирую­щий орган изменяет свое положение («Открыто-Закрыто», «Мин.-Макс.» и др.) при достижении регулируемым параметром некото­рых значений, именуемых пороговыми. Поэтому такие ре­гуляторы называют позиционными. Они бывают двух- или

трехпозиционными. Релейные регуляторы применяются при ма­лом запаздывании и большой постоянной времени объекта управ­ления.

В импульсных регуляторах содержится импульсный элемент, преобразующий непрерывное изменение регулируемого параметра в ряд импульсов, следующих друг за другом через определенные промежутки времени. Импульсы могут отличаться амплитудой, длительностью и знаком в зависимости от конструкции регулятора.

Импульсные регуляторы обычно применяют для регулирования медленно протекающих процессов в инерционных объектах со зна­чительным запаздыванием.

Задачей автоматической системы регулирования является под­держание заданных значений регулируемых величин технологиче­ского процесса или изменения их по определенному закону. В ре­зультате возникновения в системе возмущающих воздействий или изменения заданного значения регулируемой величины нарушается равновесие в системе, что вызывает переходный процесс, которыл приводит к новому равновесному состоянию. Характер переход­ного процесса определяется динамическими свойствами системы, в основе которых лежит понятие об ее устойчивости.

Устойчивость АСР. Устойчивостью называют способ­ность системы восстанавливать состояние равновесия, из которого она была выведена в результате какого-либо воздействия.

Устойчивость является одним из основных показателей АСР, определяющих ее работоспособность. Поэтому при исследовании системы необходимо проводить анализ ее устойчивости. Автомати­ческая система будет устойчивой, если ее выходная величина ос­тается ограниченной при любых ограниченных по абсолютной ве­личине входных воздействий. Система будет неустойчивой, если при сколь угодно малых отклонениях от состояния равновесия она не возвращается к нему, а совершает около него недопустимо боль­шие колебания или непрерывно удаляется от него. Такие системы не работоспособны.

Поведение автоматической системы регулирования при наличии в ней возмущающих и управляющих воздействий описывается диф­ференциальным уравнением

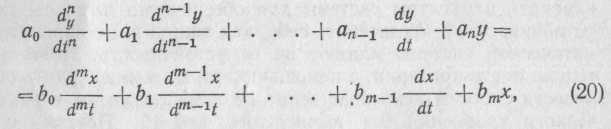
где а₀, a₁ . . . , а_п и b_о, b₁ . . . , b_m — постоянные коэффициенты. Процесс регулирования определяется решением этого диффе­ренциального уравнения (20), представляющего собой сумму част­ного решения неоднородного уравнения (20) с правой частью и об­щего решения уравнения (20) без правой части, т. е.

Первое слагаемое этого уравнения называется вынужденным решением (в случае y_част (t) = const это будет установившееся значение), а второе слагаемое — переходной составляющей.

Система будет устойчивой, если с течением времени при t переходная составляющая будет стремиться к нулю. Найдем эту составляющую из уравнения (20). Для этого необходимо решить характеристическое уравнение этой системы: а_орⁿ + а₁р^n-1 + . . . + + а_п-1p + а_п = 0. тогда общее решение уравнения (6—5) будет иметь вид:

где С_1; С₂ , . . . , С_п — постоянные коэффициенты; p_l р₂, . . . … , р_п — корни характеристического уравнения системы.

Так как по условию задачи величина y_общ(t) с течением вре­мени должна стремиться к нулю, то каждый член выражения (21) также должен стремиться к нулю. Для этого необходимо и доста­точно, чтобы вещественная часть (действительные корни могут рассматриваться как частный случай комплексных корней с нуле­вой мнимой частью) всех корней характеристического уравнения была отрицательной. В этом случае показатели степени всех экс­понент будут отрицательными, в результате чего с течением вре­мени абсолютные значения всех экспоненциальных слагаемых бу­дут стремиться к нулю.

Если хотя бы один корень характеристического уравнения имеет положительную или равную нулю вещественную часть, соответст­вующая составляющая переходного процесса Cke^Pkt будет неогра­ниченно возрастать или совершать незатухающие колебания. Сле­довательно, система не сможет прийти в установившееся состояние, т. е. система будет неустойчивой.

Таким образом, чтобы ответить на вопрос, устойчива или не­устойчива система, достаточно найти корни ее характеристического уравнения. Однако этим методом пользоваться во многих случаях практически невозможно, так как находить корни алгебраических уравнений высоких степеней очень трудно. Кроме того, найдя корни характеристического уравнения, мы определим, устойчива или неустойчива система, но не сможем установить, как нужно изменить параметры системы для обеспечения или повышения ее устойчивости, и представить себе, как те или иные параметры авто­матической системы влияют на ее устойчивость. Поэтому жела­тельно иметь критерии, с помощью которых можно судить об устой­чивости системы непосредственно по коэффициентам характеристи­ческого уравнения без вычисления корней. Поэтому в теории автоматического регулирования и инженерной практике широко применяют косвенные методы исследования системы автоматического регулирования на устойчивость. Такие критерии называются кри­териями устойчивости.

Критерии устойчивости АСР. Известны несколько таких крите­риев. Наиболее употребительны алгебраические критерии Рауса— Гурвица, основанные на рассмотрении системы неравенств, обра-

зуемых из коэффициентов характеристического уравнения, а также связанные с частотными представлениями критерии Михайлова и Найквиста.

Проверка устойчивости по критерию Рауса — Гурвица сводится к вычислению по коэффициентам характеристичес­кого уравнения так называемых определителей Гурвица, которые для устойчивой системы управления должны быть положительными. Иными словами, система устойчива, если опре­делители _{1; 2}, . . . , _n, составленные из коэффициентов урав­нения а_ор^п + а₁р^п-х + а₂р^п-2 + ...+ а_п-1р + а_п = 0, положительны при а_о>0.

Для получения определителей Гурвица составляется таблица из коэффициентов характеристического уравнения п-й степени:

Правила составления таблицы: по главной диагонали выписы­вают по порядку п коэффициентов характеристического уравнения от а₁ до а_п; каждая строка содержит п элементов; строки с нечет­ными и четными индексами чередуются; недостающие элементы строк заполняются нулями. Отчеркивая соответствующие строки и столбцы таблицы, получим п определителей Гурвица:

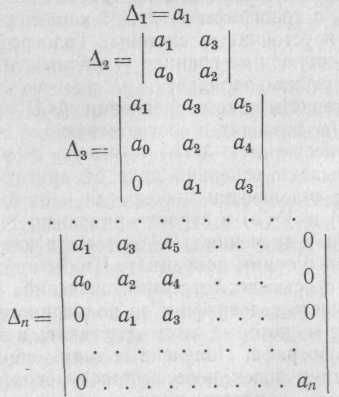
Условием устойчивости для систем первого порядка (п = 1) яв­ляется а₀ > 0, а₁ >0; второго порядка (n = 2)а_о>О, а₁>0, а₂>0; третьего порядка (п = 3) а_о>0, а₁>0, а₂>0, а₁а₂>а₃а₀.

Достоинством критерия устойчивости Payca—Гурвица являются

его сравнительная простота и небольшой объем вычислений при невысоком порядке дифференциального уравнения системы. Для систем более высокого порядка n 4 использование этого критерия затруднительно ввиду значительного объема вычислений. В таких случаях применяют другие критерии, использующие частотные характеристики АСР.

Критерий устойчивости Михайлова — это частотный критерий, основанный на построении по характеристи­ческому уравнению системы так называемой характеристической кривой, или годографа, по виду которой судят об устойчивости АСР.

Представим левую часть характеристического уравнения в виде функции от р, т. е. F (р) = а_ор^п + a₁p^n-1 + . . . +а_п-1p' +а_n.

Заменив р на j , получим уравнение комплексного вектора

Уравнение (22) можно свести к виду F (j ) = X ( ) + jY ( ), вектор его при изменении от 0 до опишет некоторую кривую, называемую годографом Михайлова, по виду которой можно су­дить об устойчивости системы.

Критерий Михайлова формулируют следующим образом: для устойчивости автоматической системы n-го порядка необходимо и достаточно, чтобы годограф Михайлова при изменении от 0 до , начиная с положительной вещественной оси, обошел после­довательно в положительном направлении (против часовой стрелки) п квадрантов комплексной плоскости.

На рис. 65, а годографы 1, 2 и 3 характеризуют устойчивые, годограф 5 — неустойчивые системы. Годограф 4 характеризует систему, находящуюся на границе устойчивости. Анализ АСР про­изводят в следующем порядке:

1. в характеристическом уравнении АСР заменяют р на j ;

2. члены с j возводят в соответствующие степени, после чего группируют вещественную X ( ) и мнимую Y ( ) части уравнения, которые выписывают отдельно друг от друга;

3. задаваясь отдельными значениями от 0 до , определяют величины X ( ) и Y ( ) и строят кривую по точкам, полученным при определенных значениях со, соответствующих точкам пересе­ чения годографа с осями координат. Чтобы найти точки пересече­ ния годографа с осью вещественных значений, нужно приравнять нулю мнимую часть годографа и из полученного уравнения найти значения частот , которые затем подставить в выражение вещест­ венной части годографа. Полученные таким образом значения яв­ ляются абсциссами точек пересечения годографа с вещественной осью. Аналогично, приравнивая к нулю вещественную часть го­ дографа, определяют ординаты точек, в которых годограф пересе­ кает мнимую ось;

4. по найденным точкам строят годограф системы и производят оценку ее устойчивости

Критерий Найквиста — Михайлова позволяет судить об устойчивости замкнутой системы регулирования по ам­плитудно-фазовой характеристике разомкнутой системы, что дает возможность использовать для оценки устойчивости результаты экспериментальных исследований.

Критерий устойчивости Найквиста—Михайлова формулируют следующим образом: замкнутая система устойчива, если ампли­тудно-фазовая характеристика разомкнутой системы не охваты­вает на комплексной плоскости точку с координатами X (со) = = —1;jY( ) = 0.

На рис. 65, б изображены амплитудно-фазовые характеристики разомкнутых систем, которые в замкнутом состоянии устойчивы —1,

Рис. 65. Характеристики систем регулирования:

а — годографы замкнутых систем регулирования; б — амплитудно-фазовые характери­стики разомкнутых систем

Рис. 66. Кривые, характеризующие качество переходных процессов: аперио­дического (а), колебательного (б)

неустойчивы — 3 или находятся на границе устойчивости — 2.

На устойчивость системы значительное влияние оказывает за­паздывание. Запаздывание в реальных технологических объектах затрудняет работу автоматических систем регулирования и ухуд­шает качество их работы. Объясняется это тем, что воздействие регулятора на вход объекта зависит от значения регулируемой величины на выходе объекта в данный момент. Однако за время, обусловленное запаздыванием, состояние объекта может изме­ниться, и воздействие регулятора, еще не воспринявшего это из­менение, может быть направлено в сторону усиления возмущений на входе объекта, а не в сторону их устранения. Запаздывание в объекте увеличивает отклонение регулируемой величины от за­данного значения, удлиняет переходный процесс и может привести к неустойчивому состоянию.

Показатели качества АСР. При определении работоспособности АСР устойчивость является необходимым, но недостаточным ус­ловием. Вторая не менее важная задача — обеспечение качества процесса регулирования.

Качество процесса регулирования оценивают качеством пере­ходных процессов и ошибками в установившихся режимах. Ка-

чество переходных процессов обычно оценивают по переходной функции, которая представляет собой реакцию системы на внешнее воздействие типа единичной ступенчатой функции.

Для следящих систем и систем программного управления пере­ходную функцию рассматривают по отношению к задающему воз­действию, а для систем стабилизации — по отношению к возму­щающему воздействию.

Из всех качественных показателей выделяют несколько наибо­лее важных, которые достаточно полно определяют качество почти всех систем регулирования. К таким показателям относят: время переходного процесса, максимальное отклонение (перерегулиро­вание) регулируемой величины от заданного значения, колебатель­ность и точность.

Качество процесса регулирования в каждом конкретном случае определяется динамическими свойствами объекта K_o6, Т_об, _об, выбранным типом автоматического регулятора (П-, И-, ПИ- и ПИД-) и установкой параметров настройки.

По виду характеристики переходный процесс может быть апе­риодическим или колебательным (рис. 66).

чем меньше величина I₁ тем выше качество регулирования.

Для колебательного переходного процесса используют квадра­тичную интегральную оценку

Временем регулирования t_p называют время, в течение которого, начиная с момента приложения воздействия к системе, отклонение регулируемой величины у (t) отличается от нового установившегося значения не более чем на = 5 % (если величина не задана). Этот показатель характеризует быстро­действие системы: чем меньше t_p, тем лучше система реагирует на внешние воздействия.

Максимальным отклонением, или перерегули­рованием а, является величина первого отклонения от за­данного значения, выражаемая в процентах от у₀. Абсолютная величина определяется с помощью кривой переходного процесса: y_макс = у₁—у₀, при этом перерегулирование будет равно: = = ( y_макс / у₀) 100%.

Величина перерегулирования не должна превышать 10—30 %.

Колебательность системы m характеризуется числом колебаний регулируемой величины за время переходного процесса. Колебательность связана со степенью затухания выражением = 1—е^{2 т} , где т — колебательность системы.

Степень затухания — одна из оценок колебатель­ности процесса. Под степенью затухания подразумевают отноше­ние разности двух соседних амплитуд колебаний, направленных в одну сторону, к первой из них = (у₁—у₂)/у₁.

Если за время регулирования число колебаний кривой переход­ного процесса будет меньше или равно заданному по условиям технологии, то считают, что по колебательности система обладает требуемым качеством регулирования.

Точность системы регулирования определяется вели­чиной отклонения установившегося значения регулируемой ве­личины от заданного. Разность между заданным и действительным значениями регулируемой величины называют статической ошиб-

кой регулирования или остаточным отклонением. Возвращение регулируемой величины к заданному значению без остаточного отклонения достигается введением в закон регулирования воздейст­вия по интегралу от отклонения регулируемой величины.

Рассмотренные выше методы оценки качества относят к прямым методам исследования — по кривой переходного процесса, кото­рая представляет собой графическое изображение решения диффе­ренциального уравнения системы. Однако часто для сложных си­стем регулирования бывает затруднительно экспериментально снять кривую переходного процесса. Поэтому часто используют косвен­ные методы оценки качества — интегральный и частотный, которые позволяют установить характер переходного процесса без построе­ния его графика.

Интегральный метод основан на вычислении опреде­ленных интегралов без решения дифференциальных уравнений системы. Для переходных процессов без перерегулирования ка­чество регулирования оценивается по величине площади, заключен­ной между кривой переходного процесса и осями координат:

Этот интеграл определяет качество процесса регулирования по квадратичной сумме площадей, заключенных между кривой пере­ходного процесса и осями координат. Чем меньше I₂, тем выше качество переходного процесса.

Частотный метод предполагает наличие зависимости ка­чества регулирования от вида вещественной частотной характери­стики системы

При расчете используют аппроксимированные вещественные частотные характеристики.