§ 33. Классификация звеньев по динамическим свойствам

При решении задач анализа и синтеза автоматическую систему разбивают на отдельные части, математическая зависимость между входными и выходными величинами которых и временем описы­ вается дифференциальными уравнениями не выше второго порядка. Такие искусственно выделенные части автоматической системы на­ зывают элементарными динамическими звеньями. В отличие от элемента динамическое звено необя­ зательно является конструктивной или схемнозаконченной частью системы. Одному элементу (например, исполнительному механизму) могут соответствовать несколько динамических звеньев.

При представлении элементов системы в виде элементарных динамических звеньев не важен принцип построения элемента. Элементы различной физической природы могут быть представ­лены в виде одинаковых динамических звеньев, если их динамиче­ские свойства описываются одинаковыми дифференциальными урав­нениями. Поэтому при решении задач анализа и синтеза автомати­ческих систем многообразие элементов автоматики сводится к не­скольким типовым элементарным динамическим звеньям.

Существуют 6 типовых элементарных динамических звеньев: усилительное, апериодическое, колебательное, интегрирующее, диф­ференцирующее и чистого запаздывания.

Усилительное звено. Это простейшее звено, которое образуется в случае передачи входного сигнала на выход без каких-либо за­медлений или ускорений во времени, т. е. переходные процессы в звене отсутствуют. Примеры усилительных звеньев приведены на рис. 60, а—в.

Свойства этого элемента описываются уравнением у = Кх, где К — коэффициент усиления звена.

Рис. 60. Усилительные и апериодические звенья:

а — рычажная передача; б — зубчатая пара; в — усилитель; г — пассивный четырех­полюсник; д — термопара; е — магнитный усилитель; ж — электродвигатель

Передаточная функция звена представляет собой постоянную величину W (р) = К.

Амплитудно-фазовая характеристика усилительного звена также равна постоянной величине W (j ) = К, при этом амплитудно-частотная характеристика А ( ) = К, а фазочастотная характе­ристика ( ) = 0. Графически АФХ изображается в виде точки на вещественной оси комплексной плоскости на расстоянии К от начала координат.

Апериодическое звено. Звено называется апериодическим, если его входная и выходная величины связаны между собой дифферен­циальным уравнением

T(dy)/dt + y = Kx.

Примеры апериодических звеньев приведены на рис. 60, г—ж. В операторной форме это уравнение может быть записано как

(Tp+1)Y(p) = KX(p),

тогда передаточная функция звена имеет вид

W(p) = K/(Tp+1).

Если на вход звена Подать ступенчатое воздействие, то времен­ная характеристика будет иметь вид

Заменив р на j , получим АФХ апериодического звена

При Т₁ = 2Т₂ получают вещественные и равные корни уравне­ния а временная характеристика за­писывается выражением

АЧХ апериодического звена имеет вид

а ФЧХ этого звена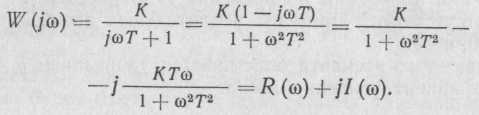

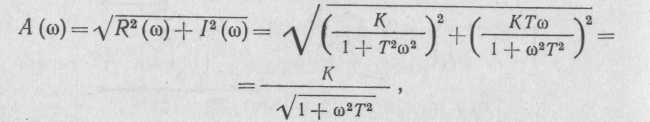
Колебательное звено. Колебательным называется звено, у ко­торого выходные и входные величины связаны следующим диффе­ренциальным уравнением:

которое в операторном виде записывается как

Передаточная функция колебательного звена имеет вид

где К — коэффициент усиления звена; Т₁иТ₂ — постоянные вре­мени звена; при Т₂ = 0 звена превращается в апериодическое.

Примеры некоторых колебательных звеньев приведены на рис. 61.

В зависимости от соотношения между постоянными времени Т₁ и Т₂ корни характеристического уравнения будут вещественными, мнимыми или комплексно-сопряженными. В соответствии с этим и временная характеристика звена будет иметь апериодический или колебательный характер.

При Т₁>2Т₂ получают вещественные и разные корни р₁ = ₁ и р₂ = ₂ характеристического уравнения, тогда временная ха­рактеристика звена имеет вид

При Т₁ 2Т₂ переходные процессы в звене протекают аперио­дически и такое звено не является колебательным. Оно может быть представлено в виде последовательного соединения двух апериоди­ческих звеньев.

При T₁<2Т₂ корни уравнения будут комплексными p_1,2 =

= ±j , где

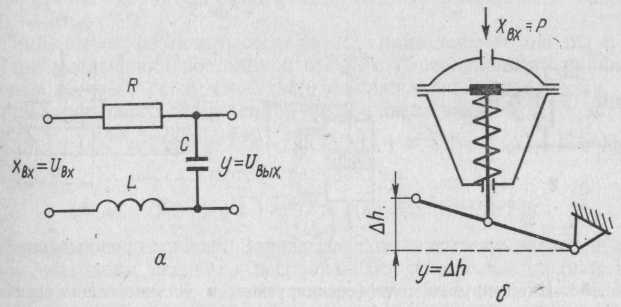
Временная характеристика такого звена

Рис. 61. Колебательные звенья:

а — пассивный четырехполюсник; б — мембранный исполнительный механизм

При Т₁ = 0 в колебательном звене возникают незатухающие колебания. АФХ колебательного звена имеет вид

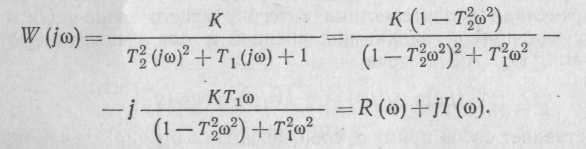
Амплитудно-частотная и фазочастотная характеристики коле­бательного звена:

Интегрирующее звено. Звено называется интегрирующим, если выходная величина пропорциональна интегралу от входной ве­личины.

Дифференциальное уравнение интегрирующего звена имеет вид

T(dy)/(dt) = Kx.

где = K/T — скорость разгона.

Интегрируя это уравнение, получим

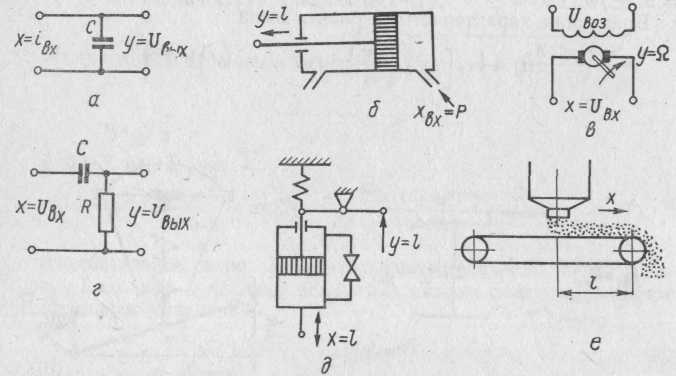
Рис. 62. Интегрирующие, дифференцирующие и запаздывающие звенья:

а— пассивный четырехполюсник; б — гидравлический исполнительный механизм; в—электродвигатель; г - пассивный четырехполюсник; д - спокоитель с пружиной в ме­ханических цепях; е — ленточный конвейер

Примеры некоторых интегрирующих звеньев приведены на рис. 62, а—в.

Передаточная функция такого звена: W (р) = /р.

Временная характеристика интегрирующего звена у (t) = x_ot имеет вид прямой линии, наклоненной к оси абсцисс под углом а = arctg x₀. АФХ звена

представляет собой прямую, совпадающую с отрицательной мнимой осью характеристики. Амплитуда выходных колебаний звена А ( ) = / убывает с частотой, а фаза = — /2. Таким обра­зом, интегрирующее звено при всех частотах создает отставание выходных колебаний от входных на 90°.

Дифференцирующее звено. Динамическая характеристика этого звена описывается дифференциальным уравнением вида у =

= К (dx)/(dt), и передаточная функция этого звена равна

W (р) = Кр.

Дифференцирующее звено представляет собой устройство, ко­торое на выходе дает величину, производную по времени от входной величины. Однако на практике осуществить такое идеальное диф­ференцирующее звено невозможно, так как все физические про­цессы в природе в той или иной степени инерционны, а в соответст­вии с уравнением этого звена скачкообразное изменение входной величины должно вызвать мгновенное изменение выходной вели­чины от 0 до и немедленный спад ее до 0. В системах регулиро­вания применяют звенья, которые выполняют дифференцирующее действие приближенно; они называются реальными диффе­ренцирующими звеньями. Уравнение такого звена имеет вид

T(dy)/(dt) + y = KT(dx)/(dt),

а передаточная функция такого звена W (р) = (КТр)/(Тр + 1).

Временная характеристика реального дифференцирующего звена у (t) = Кх_ое^—(t/T).

Примеры дифференцирующих звеньев приведены на рис. 62, г, д.

При уменьшении постоянной времени Т реальное дифференци­рующее звено по своим свойствам приближается к идеальному.

АФХ реального дифференцирующего звена имеет вид

а АЧХ и ФЧХ определяются уравнениями:

Запаздывающее звено. Запаздывающим называют звено, в ко­тором выходная величина воспроизводит изменение входной ве­личины без искажений, но с некоторым постоянным запаздыванием : y(t) = x (t— ).

Передаточная функция запаздывающего звена: W(p) = e^—p/ .

Примером запаздывающего звена может служить ленточный конвейер (рис. 62, е), который загружают с одного конца материа­лом, поступающим из бункера.

АФХ такого звена

W(j )=e^—j

Графически ее представляют в виде окружности единичного радиуса А ( ) = 1 с центром в начале координат.