§ 13. Вычислительные и логические элементы

Разнообразие задач управления предопределяет необходимость использования в системах различных классов вычислительных и логических элементов автоматики.

Все вычислительные счетно-решающие устройства разделяются на аналоговые (непрерывного действия) и цифровые (дискретного действия).

Аналоговые вычислительные устройства. В этих устройствах все математические величины, участвующие в решении задачи, представлены в некотором масштабе непрерывно изменяющимися физическими величинами: перемещениями, углами поворота, на­пряжениями, токами и др. Устройства этого типа являются физи­ческими системами (механические, электрические и др.), в которых протекают процессы, описываемые уравнениями, подобными урав­нениям задачи, подлежащей решению. Таким образом, аналого­вые вычислительные устройства являются математическими мо-

При большом К последний член в уравнении (2) стремится к нулю. Тогда U_вых будет связано с U_BX следующей зависимостью

делями изучаемых процессов. Отсюда другое название этих уст­ройств — моделирующие.

Широкое распространение получили электронные моделирую­щие устройства. Это объясняется, с одной стороны, пригодностью одних и тех же математических уравнений для описания объектов и явлений различной физической природы, с другой — тем, что этот вид аналоговых устройств удобен в управлении, компактен и обладает гибкой структурой.

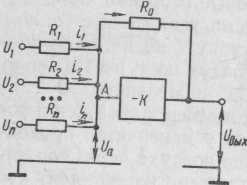
Электронные устройства обеспечивают решение обыкновенных дифференциальных уравнений любого порядка. В состав этих уст­ройств входят следующие блоки: интегрирующие, суммирующие, множительные; осуществляющие масштабное преобразование; функ­циональные для образования нели­нейных функций и ряд вспомо­гательных блоков, обеспечивающих возможность наблюдения и ре­гистрации решения и управления устройством.

Рис. 25. Структурная схема

операционного суммирующего

усилителя

Математические операции в таких электронных моделях выполняются с помощью операционных (решаю­щих) усилителей, которые являются основными базовыми элементами ана­логовых вычислительных устройств. Операционные усили­тели — это усилители постоян­ного тока с очень большим коэффициентом усиления К (несколько десятков тысяч), охваченные отрицательной обратной связью. В электронных моделях процессов используются суммирующие, инвертирующие, интегрирующие и дифференцирующие усилители, построенные на основе операционных усилителей. Структурная схема суммирующего усилителя приведена на рис. 25. Составим уравнение для суммы токов в узле А. Так как входное сопротивле­ние операционного усилителя велико, входным током можно пренебречь. Учитывая, что i_j = (U_j — U_a)/R_j, i₀ = (U_a—U_вых)/R₀ и U_a = -U_вых/K,

получим =i₀

Таким образом, операционный усилитель будет умножать вход-ные напряжения (а значит, и представляемые ими моделирующие величины) на коэффициент R₀/Rj и затем их складывать.

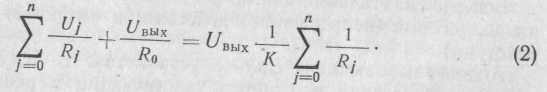
Если в схеме суммирующего усилителя вместо R_o включить конденсатор, то получится интегрирующий усилитель, причем при наличии у него нескольких входов происходит интегрирование суммы. Если в схеме суммирующего усилителя вместо сопротивле­ний Rj включить конденсаторы, то получим дифференцирующий усилитель.

Соединяя определенным образом различные блоки аналоговых вычислительных устройств, можно получать различные электрон­ные модели, довольно точно описывающие явления, протекающие в технологических объектах.

Вычислительные устройства дискретного действия. В них все математические величины представляют в виде дискретных значе­ний. Вычисление заключается в последовательном выполнении арифметических операций. В устройствах этого типа широко при­меняют логические элементы, триггеры, регистры, счетчики, де­шифраторы и т. д.

Для решения сложных задач управления технологическими про­цессами в системах автоматики используют различные логиче­ские элементы. К логическим элементам относятся схемы, реализующие основные логические функции — И, ИЛИ и НЕ. Поскольку любая сложная логическая функция может быть вы­ражена через элементарные функции И, ИЛИ и НЕ, система логи­ческих элементов И, ИЛИ и НЕ называется функционально пол­ной. Иногда в качестве типовых используют и более сложные эле­менты, реализующие логические функции И—НЕ, ИЛИ—НЕ и др., позволяющие строить более сложные комбинационные схемы для управления технологическими объектами.

К логическим элементам, выполняющим основные логические функции, относятся схемы НЕ, И (схема совпадения) и ИЛИ (схема собирательная).

С помощью схемы НЕ реализуется логическая функция НЕ (от­рицание). Эта схема выполняется на активных элементах — реле, транзисторах и т. д. На рис. 26, а показана схема НЕ, выполнен­ная на транзисторе: положительный сигнал на ее выходе (коллек­торе транзистора) будет только при отрицательном сигнале на ее входе.

С помощью схемы совпадения реализуется логическая функция И (конъюнкция). Схема совпадения, выполненная на пассивных элементах (диодах), показана на рис. 26, в. На выходе этой схемы сигнал будет только в том случае, если есть сигналы на обоих вхо­дах одновременно. В этом случае диоды Д запираются и через со­противление R_K в цепи коллектора не протекает ток; на выходе схемы высокое положительное напряжение. Отсутствие положи­тельного сигнала хотя бы на одном из входов схемы приводит к от­крыванию одного из диодов, появлению тока через сопротивление R_k и, как следствие,— падению напряжения на выходе схемы.

С помощью собирательной схемы реализуется функция ИЛИ (дизъюнкция). Эта схема показана на рис. 26, д. Сигнал на выходе схемы появится только тогда, когда есть сигнал- хотя бы на одном из входов.

Триггер представляет собой устройство, с помощью ко­торого можно записывать, хранить и считать двоичную информа­цию. Триггер имеет два устойчивых состояния равновесия. Од­ному из этих состояний приписывается значение 1, а другому — 0. Состояние триггера распознается по его выходному сигналу. Под влиянием входного сигнала триггер скачкообразно переходит из одного устойчивого состояния в другое, при этом скачкообразно изменяется уровень напряжения его выходного сигнала.

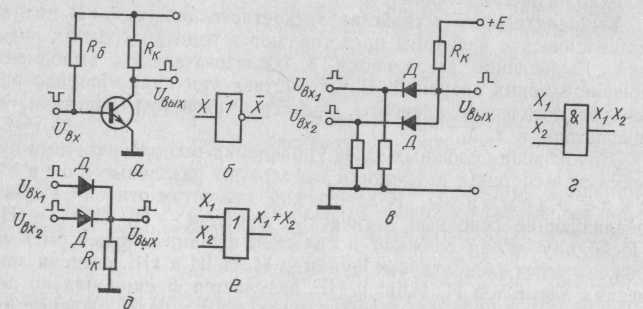
Рис. 26. Логические элементы автоматики: схема НЕ (а), ее условное обозна­чение (б); схема И (в), ее условное обозначение (г); схема ИЛИ (д), ее услов­ное обозначение (e)

Для удобства использования в схемах вычислительных уст­ройств триггеры обычно имеют два выхода: прямой Q (называемый также «выход 1») и инверсный («выход 0»). В единичном состоя­нии триггера на выходе Q высокий уровень сигнала, а в нулевом — низкий. На выходе — наоборот.

Простейшим триггером является асинхронный RS-триггер, вы­полненный на двух логических элементах ИЛИ—НЕ. Логическая структура и его условное обозначение приведены на рис. 27, а, б.

Такой триггер образован из двух комбинационных схем ИЛИ— НЕ, соединенных таким образом, что возникают положительные обратные связи, благодаря которым в устойчивом состоянии вы­ходной транзистор одной схемы ИЛИ—НЕ закрыт, а другой от­крыт.

Полученный таким образом триггер имеет два входа: S — установки триггера в 1 и R — установки триггера в 0.

Рассмотрим прежде всего воздействие на такой триггер комби­нации сигналов S = 1, R = 1 и S = 0, R = 0.

Сочетание S = l, R = 1 является запрещенным, так как при _нем на обоих выходах триггера устанавливаются логические 0 _и после снятия входных сигналов состояние его непредсказуемо.

Для элемента ИЛИ—НЕ логический 0 является пассивным сиг­налом, с поступлением его на вход состояние выхода элемента не изменяется. Поэтому комбинация S = 0, R = 0 не изменяет со­стояние триггера.

Логическая 1 для элемента ИЛИ—НЕ является активным сиг­налом: наличие ее на входе однозначно определяет на выходе ло­гический 0 вне зависимости от сигнала на другом входе. Отсюда

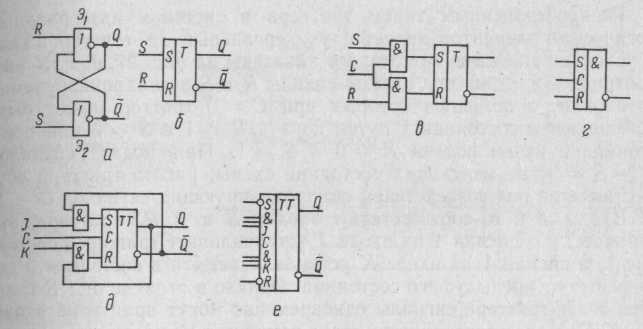
Рис. 27. Функциональные схемы триггеров: асинхронного .RS-триггера (а),

его условное обозначение (б); синхронного RS-триггера (б); его условное

обозначение (г); .JK-триггера (д), его условное обозначение (е)

следует, что переключающим сигналом для рассматриваемого триг­гера является логическая 1, а также то, что вход S (установка триггера в состояние Q = 1) должен быть связан с элементом, вы­ход которого принят за (см. рис. 27, а).

Для переключения триггера в состояние Q = 1 на его входы следует подать комбинацию S=1, R = 0, а для переключения в состояние Q = 0 — S = 0, R = 1.

Пусть триггер находится в состоянии 0 (Q = 0, = 1), а на его входах действуют сигналы S = 0, R = 0. Для переключения его в состояние Q = 1 подадим на входы комбинацию S = 1, R = 0. Тогда на выходе элемента Э₂ установится логический 0, на входах элемента Э₁ будут одновременно действовать логические 0 и на выходе Q установится логическая 1 — триггер переключается в новое состояние (Q = 1, = 0). Для его переключения из этого состояния на входы должна поступить комбинация S = 0, R = 1. После этого на выходе Q будет логический 0, на входах элемента Э₂ одновременно окажутся логические 0 и его выход примет потен­циал, соответствующий = 1 — триггер переключается в состоя­ние Q = 0, = 1.

Часто необходимо, чтобы в вычислительных устройствах триг­гер реагировал на входные сигналы только в определенные моменты времени. Эти моменты обычно задаются с помощью дополнитель­ного — входного — сигнала синхронизации С. На рис. 27, в, г приведены схема и условное обозначение такого синхронного RS-триггера. Она содержит асинхронный RS-триггер Т с прямыми входами и две схемы совпадения. Последние передают переключаю­щую логическую 1 с информационного S- или S-входа на соответст­вующие входы Т только при наличии на синхронизирующем входе С логической 1. При С = 0 информация с S- и R-входов на триггер не передается.

Распространенным типом триггера в системах интегральных логических элементов является универсальный JK-триггер, схема и условное обозначение которого показаны на рис. 27, д, е. У рас­сматриваемого триггера имеются входы R и S несинхронизируемой установки, с помощью которых при С = 0 триггер может быть установлен в состояние 1 путем подачи R = 1 и S = 0 или в со­стояние 0 путем подачи R = 0 и S = 1. При подаче сигналов R = S = 1, не меняющих состояние схемы, работа триггера осу­ществляется под воздействием синхронизирующих сигналов С =1. Входы J и К соответствуют входам S и R RS-триггера, это означает, что сигнал 1 на входе / устанавливает триггер в состоя­ние 1, а сигнал 1 на входе K устанавливает его в состояние 0 не­зависимо от предыдущего состояния. Однако в отличие от RS-триг-гера в JK-триггере сигналы одновременно могут прийти на входы J и К. При этом состояние триггера изменится на противоположное, т. е. при J = К схема ведет себя как триггер со счетным входом. Регистром называется функциональное устройство, пред­назначенное для приема и запоминания двоичных чисел, а также для некоторых их логических преобразований.

Параллельный регистр выполняет функции записи и хранения параллельного двоичного кода. Для построения такого регистра могут быть использованы ^5-триггеры. На рис. 28, а приведена функциональная схема параллельного регистра.

Параллельный двоичный код подается на входы х₁—х_п тригге­ров. Запись производится положительными импульсами, подавае­мыми на входы С триггеров. Код снимается с выходов Q₂—Q_n. Для установки регистра в 0 используют входы R-триггеров.

В этой схеме запись информации в регистр синхронизируется по входу С и происходит только в момент подачи на вход С положи­тельного импульса. Работой регистра управляют две шины: уста­новки нуля и приема информации. Прежде чем записать информа­цию в регистр, необходимо подать управляющий сигнал на шину установки 0, т. е. все триггеры регистра установить в состояние 0. Для приема информации в регистр необходимо подать управ­ляющий синхронизирующий сигнал на шину приема и одновре­менно по информационным цепям, соединенным с единичными уста­новочными входами триггеров, подать код записываемого числа в регистр.

Счетчик предназначен для счета поступающих на его вход импульсов, в интервале между которыми он должен хранить ин­формацию об их числе. Поэтому счетчик состоит из запоминающих ячеек — триггеров. Ячейки счетчика соединяют таким образом, чтобы каждому числу импульсу соответствовали единичные со­стояния определенных ячеек. При этом совокупность единиц и нулей на выходах п ячеек счетчика представляет собой n-разряд­ное двоичное число, которое однозначно определяет число прошед­ших на входе импульсов. Поэтому ячейки счетчика называют его разрядами.

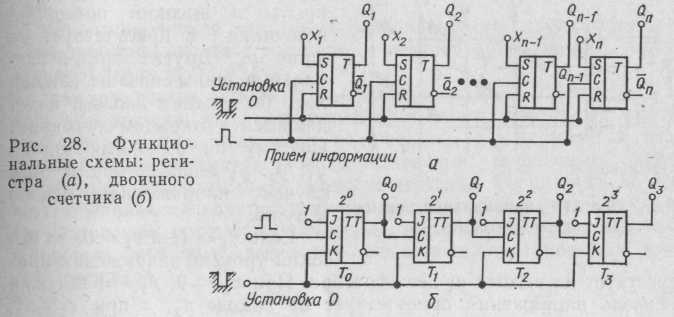
На рис. 28, б представлена схема четырехразрядного двоичного счетчика прямого счета с цепями последовательного переноса и им­пульсным входом. Входные импульсы положительной полярности подаются на счетный вход С триггера младшего разряда счетчика Т_о. Перед началом счета сигнал установки нуля устанавливает в со­стояние 0 все триггеры счетчика. По первому входному импульсу триггер Т_о переключается в состояние 1 и код в счетчике прини­мает значение х = 0001. Это значение кода сохраяется до прихода следующего импульса. Под воздействием второго сигнала триггер Т_о переходит в состояние 0. При переходе триггера Т_о из единич­ного состояния в нулевое с прямого выхода триггера Т_о образуется положительный сигнал переноса (импульс), поступающий на счет­ный вход триггера Т_1, который установит этот триггер в состоя­ние 1. Код счетчика принимает значение х = 0010 и т. д.

Максимальное число, которое может быть зафиксировано в двоичном счетчике, определяется по формуле N =2ⁿ—1, где п— число разрядов счетчика.

Дешифратором называется логическая схема, преобра­зующая двоичный код числа, поступающего на его входы, в управ­ляющий сигнал только на одном из его выходов. Другими словами, дешифратор представляет собой совокупность схем совпадений, формирующих управляющий сигнал на одном из выходов, в то время как на остальных выходах сигналы отсутствуют.

Принципиальная схема дешифратора с логическими элементами совпадения на диодах на два входа показана на рис. 29. Горизон­тальные и вертикальные шины соединяются в определенных ме­стах диодами, которые образуют сетку (матрицу) дешифратора. Резистор и два диода, подключенные к вертикальному проводу, образуют логический элемент И. Таких схем в сетке — четыре.

Если х₁ = 0 и х₂ = 0, то триггеры регистра находятся в поло­жении, при котором на нулевых выходах триггеров высокий по­тенциал. В этом случае диоды, связанные с левой вертикальной шиной дешифратора, за­крыты и высокий потенциал источника +Е присутствует на шине у₀. Другие три верти­кальные шины связаны каждая хотя бы с одним диодом, нахо­дящимся в открытом состоянии. Поэтому на выходных шинах y₁, y₂, y₃ дешифратора в этом случае напряжение близко к нулю.

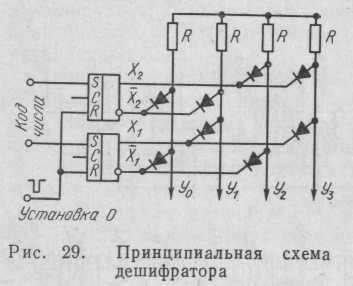
Если x₁=1, а х₂ = 0, то вы­сокий уровень напряжения при­сутствует на выходе y₁ дешифратора. При x₁= 0, х₂ = 1 высокий уровень напряжения присутствует на выходе y₂, а при x₁ = 1, х₂ = 1 на выходе у₃.