Вопросы и упражнения для самоконтроля:

1. Дайте определение производной функции.

2. В чем состоит геометрический смысл первой производной.

3. В чем состоит физический смысл первой производной.

4. Дайте определения второй производной функции.

5. В чем состоит физический смысл второй производной?

6. Сформулируйте условие возрастания и убывания функции.

7. Как найти экстремумы функции?

8. Как найти наименьшее и наибольшее значения функции на отрезке?

9. Сформулируйте условие выпуклости и вогнутости кривой.

10. Что такое асимптота? Виды асимптот.

11. Что такое дифференциал функции?

12. Найдите производные функций:

а) f (X) = ln (sin 2X) + tgX + ;

б) f (X) = е^tgX – 8X

13. Найти экстремумы функций:

а) Y = Х ² – 4;

б) Y = Х ³ – Х.

Методы нахождения интегралов

Пример 7. Найти неопределенный интеграл .

Решение:

Данный интеграл будем находить методом подстановки (заменой переменной).

1. Введем новую переменную t = Х ² + 1

2. Найдем дифференциал от подстановки (переменной):

dt = 2XdX

3. В подынтегральном выражении переменную Х заменим на t:

4. Полученный интеграл – табличный, находим его и возвращаемся к старой переменной:

где С – константа интегрирования.

Пример 8. Найти неопределенный интеграл .

Решение:

Этот интеграл будем находить методом по частям.

1. Запишем формулу интегрирования по частям

2. Разобьем подынтегральное выражение на две части, причем, одну часть обозначаем U = X, а другую dV = SinХdX.

3. Найдем функцию V = и дифференциал dU = dX.

4. Подставим V и dU в формулу интегрирования по частям и находим интеграл:

Пример 9. Найти определенный интеграл .

Решение:

Вычислим этот интеграл, используя таблицу простейших интегралов и основные свойства определенного интеграла.

Применение определенного интеграла для определения площадей плоских фигур

Пример 10. Вычислить площадь плоской фигуры, ограниченной линиями Y = Х ² и Y = Х.

Решение:

1. Построим графики этих функций, которые ограничивают площадь плоской фигуры (см. Рис.3).

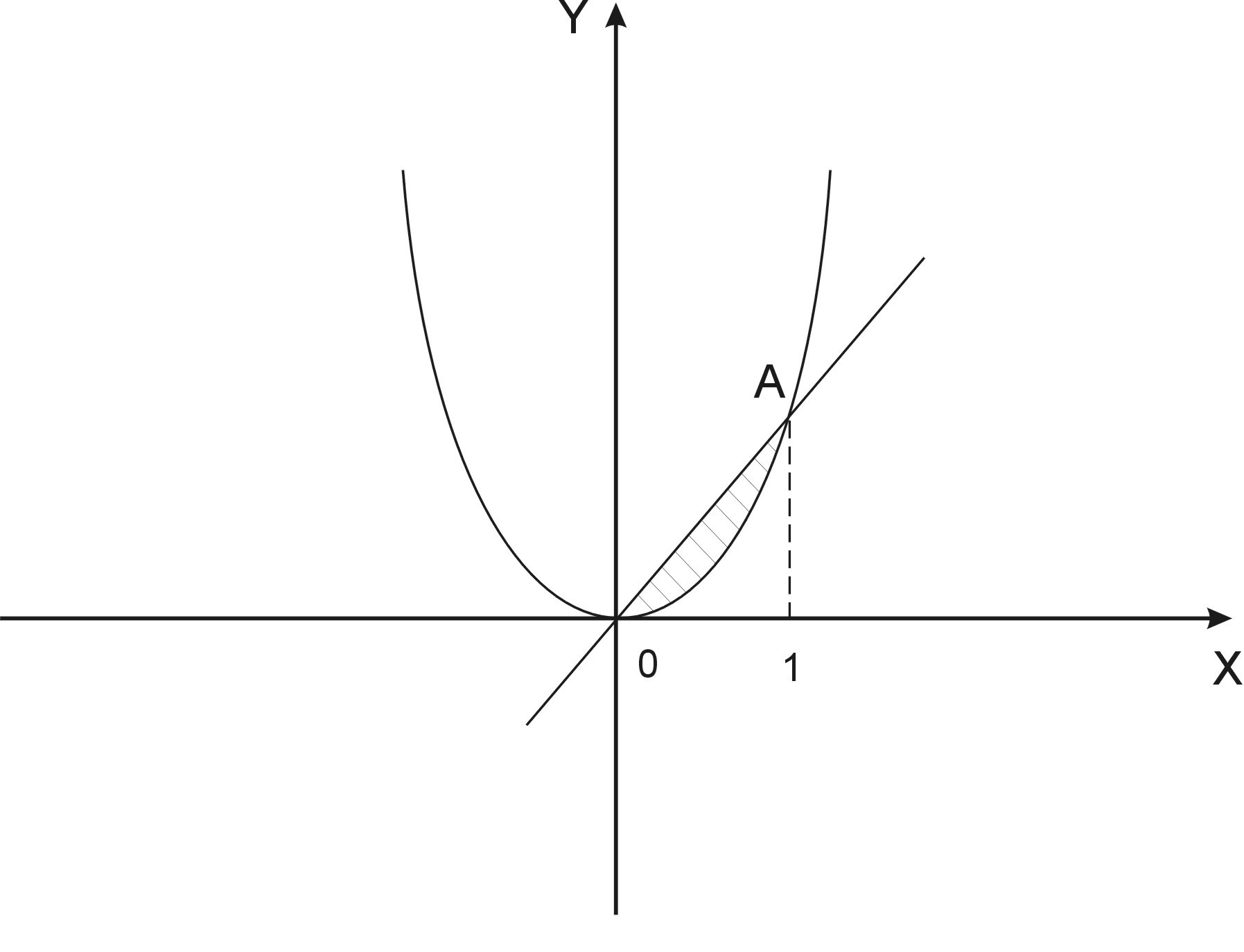
Рис.3. Нахождение площади плоской фигуры, ограниченной двумя линиями.

2. Определим пределы интегрирования. Для этого найдем точки пересечения этих линий, решая систему уравнений:

Получим уравнение Х² = Х. Решив это уравнение, находим корни:

X₁ = 0 и X₂ = 1.

Это есть точки пересечения графиков и пределы интегрирования.

3. Запишем формулу для нахождения площади нашей фигуры и вычислим ее:

S = S (площадь прямоугольного треугольника) – S (площадь криволинейного треугольника) (см. Рис. 3)

S =

Ответ: S = 1 / 6 кв. ед.

Вопросы и упражнения для самоконтроля:

1. Какое действие называется интегрированием?

2. Какая функция называется первообразной для функции f(X)?

3. Дайте определение неопределенного интеграла.

4. Перечислите основные свойства неопределенного интеграла.

5. Каким действием можно проверить интегрирование?

6. Напишите основные формулы интегрирования (табличные интегралы).

7. Дайте определение неопределенного интеграла.

8. В чем заключается геометрический смысл определенного интеграла?

9. Найдите интегралы:

а) [(1 – sin²X) / sin²X] dX; б) (1 – Х)³ dX;

в) [( Х cos X – 2 ) / Х] dX; г) [е^Х / (е^Х + 1) ] dX;

д) (10 X – Х^4/3 + 5) dX.

10. Сделать чертеж и вычислить площадь фигуры, ограниченной линиями

а) Y = (Х + 3) (Х – 2) и осью OX;

б) Y = Х³, Y = X.