Тема 3.3. Дифференциальные уравнения
Понятие дифференциального уравнения. Дифференциальное уравнение первого порядка с разделяющимися переменными, его общее и частное решение.
Однородные уравнения первого порядка. Линейное дифференциальное уравнения первого порядка. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Основная литература: [5, 8].
Дополнительная литература: [14, 6].
Тема 3.4. Ряды
Понятие числового ряда. Сходящиеся и расходящиеся числовые ряды. Необходимый признак сходимости числового ряда. Ряды с неотрицательными членами. Признаки сходимости: признак сравнения, признак Даламбера, интегральный признак. Знакопеременные ряды. Абсолютная и условная сходимости рядов. Признак сходимости знакопеременного ряда. Степенные ряды. Интервал сходимости. Разложение функции в степенные ряды. Ряд Маклорена. Ряд Тейлора. Ряды Фурье.
Основная литература: [4, 5].
Дополнительная литература: [2, 4].
Раздел 4.Теория вероятностей и математическая статистика Тема 4.1. Основные понятия и теоремы теории вероятностей
Испытания, события, виды событий, система элементарных событий. Классическое определение вероятности. Относительная частота появления события. Примеры вычисления вероятностей.
Теоремы сложений вероятностей несовместимых и совместимых событий. Теоремы умножения вероятностей независимых и зависимых событий. Противоположенные события. Вероятность появления хотя бы одного из независимых событий.
Формула полной вероятности. Формула Байеса.
Повторение независимых испытаний. Формула Бернулли.
Основная литература: [4 –7].
Дополнительная литература: [5].
Тема 4.2. Случайные величины
Понятие случайных величин, их виды. Закон распределения дискретной случайной величины. Многоугольник распределения. Основные характеристики дискретной случайной величины и их смысл: математическое ожидание, дисперсия и среднее квадратическое отклонение. Свойства математического ожидания и дисперсии. Функции распределения вероятностей непрерывной случайной величины. Плотность распределения вероятностей непрерывной случайной величины. Нахождение основных характеристик непрерывно распределенной случайной величины.
Нормальный закон распределения непрерывной случайной величины.
Вероятность попадания нормально распределенной случайной величины в заданный промежуток. Вероятность заданного отклонения для нормально распределенной случайной величины.
Основная литература: [4 –7].
Дополнительная литература: [5].
Тема 4.3. Основы выборочного метода
Сущность выборочного метода. Статистического распределение выборки, его графическое изображение в виде полигона и гистограммы. Основные характеристики выборочного распределения: выборочная средняя, дисперсия и среднее квадратическое отклонение.
Основная литература: [4 7].
Дополнительная литература: [5].
Тема 4.4. Проверка статистических гипотез
Статистические гипотезы. Сравнение двух дисперсий нормальных генеральных совокупностей. Сравнение двух средних генеральных совокупностей, дисперсии которых известны (большие независимые выборки). Сравнение двух средних генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки).
Основная литература: [4 7].
Дополнительная литература: [5].
Методические рекомендации по выполнению заданий контрольной работы
Аналитическая геометрия
Даны координаты вершин треугольника АВС: А( - 2; 7), В(10; - 2), С(8; 12). Построить чертеж и найти: а) длину стороны АВ; б) уравнение высоты, проведенной из вершины С и ее длину; в) уравнение медианы, проведенной из вершины С; г) уравнение прямой, проходящей через вершину С параллельно стороне АВ; д) площадь треугольника.
На прямоугольной системе координат строим чертеж.
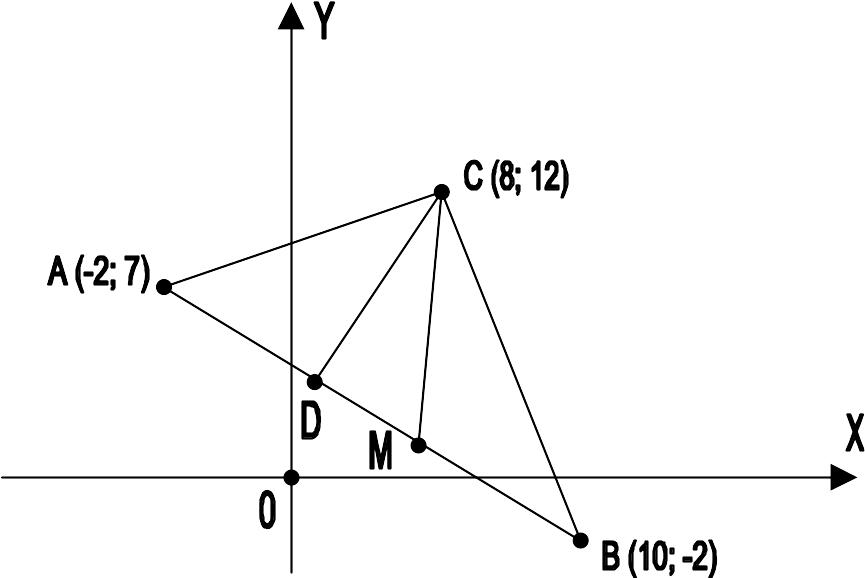
Рис. 1. Чертеж к задаче по аналитической геометрии
а) для нахождения длины АВ используем формулу:
ℓ2AB = ( X2 – X1 )2 + ( Y2 – Y1 )2, где X1 = – 2, Y1 = 7, X2 = 10, Y2 = – 2
ℓAB
=
= 15
б) для составления уравнения прямой АВ воспользуемся формулой
(Y – Y1) /(Y2 – Y1) = (X – X1) /(X2 – X1) => (Y – 7) /(– 9) = (X – 2 ) / 12 =>
12Y – 84 = – 9X – 16 => Y = – (3/4)X + 11/2, где kAB = – ¾
Уравнение высоты СД найдем:
Y – YС = kСД ( X – XС) , где kСД = – ℓ/ kAB = 4/3, Y = (4/3)X + 4/3
Для нахождения ℓСД необходимо знать координаты точки Д, которые можно найти, решив систему уравнений:
Точка Д имеет координаты (2; 4), а ℓСД = 10.
в) для нахождения медианы СМ определим координаты точки М, как середины отрезка АВ: М (4; 2,5). Будем иметь:
(Y – YМ) /(YС – YМ) = (X – XМ) / (XС – XМ) => (Y – 2,5) / 9,5 = (X – 4) / 4 => 4Y – 10 = 9,5X – 38 => Y = (19/8)X – 7
г) найдем уравнение прямой линии, проходящей через точку С параллельно стороне АВ. Используем уравнение:
Y – YС = kАД (X – XС), где kАД = – 3/4, Y = – (3/4)X + 18
д) площадь S треугольника АВС равна: S = (1/2) ℓAB ℓCД = 75 (кв. ед.)