
Ташлыкова-Бушкевич - Физика. В 2 ч. Ч. 2. Оптика. Квантовая физика. Строение и физические свойства вещества (2014)
.pdf
26.6. Задание состояния частицы в квантовой физике: пси-функция, ее физический смысл как амплитуды вероятности. Нормировка. Стандартные условия.
Суперпозиция состояний в квантовой физике
Для описания волновых свойств микрочастиц применяют вероятностный подход, так как наблюдение волновых явлений несовместимо с представлением о движении частицы по классической траектории. Переход к вероятностному описанию позволяет совместить волновые и корпускулярные свойства материи.
Из опытов по дифракции электронов, например из опытов Дэвиссона – Джермера (см. рис. 26.1), следует, что волновые свойства характерны для отдельных микрочастиц. Кроме того, эти опыты указывают на то, что квадрат модуля амплитуды волн де Бройля в данной точке пространства является мерой того, что частица обнаруживается в этой точке. Там, где интенсивность волн де Бройля больше, регистрируется большее число частиц.
Для описания состояния квантовой системы в данный момент времени вводится комплексная волновая функция (пси-функция) Ψ(x, y,z,t) . Она определяется так, что вероятность dP нахождения частицы в некоторый момент времени в элементе объема dV прямо пропорциональна Ψ 2 и элементу объема dV :
dP = |
|
Ψ |
|
2 dV = |
|
Ψ |
|
2 dx dydz, |
(26.6) |
|
|
|
|
где Ψ 2 = ΨΨ*, Ψ* – функция, комплексно сопряженная с Ψ. Волновую функцию Ψ называют амплитудой вероятности. Пси-функция непосредственно не измеряется на опыте.
При этом Ψ 2 задает интенсивность волн де Бройля и является экспе-
риментально наблюдаемой величиной. |
|
||||||||
Физический смысл квадрата модуля функции Ψ: |
|
Ψ |
|
2 |
– это плотность |
||||
|
|
||||||||
вероятности P , т.е. вероятность нахождения частицы в точке простран- |
|||||||||
ства с координатами х, y, z в момент времени t: |
|
||||||||
P = |
|
Ψ |
|
2 = ΨΨ*. |
(26.7) |
||||
|
|
||||||||
Данная вероятностная интерпретация волновой функции – один из основных постулатов квантовой механики (М. Борн, 1926).
Пси-функция определяется с точностью до произвольного постоянного множителя, т.е. функции Ψ и CΨ описывают одно и то же состояние частицы. Пси-функция должна удовлетворять условию нормировки:
81
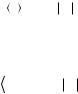
+∞ |
|
||||
∫ |
|
Ψ(x, y,z,t) |
|
2 dV =1, |
(26.8) |
|
|
||||
−∞ |
|
||||
|
|
|
|
|
|
где интеграл берется по всему пространству (−∞, +∞) . В этом случае пси-функция Ψ называется нормированной.
Условие нормировки волновой функции (26.8) означает, что пребывание частицы где-либо в бесконечном трехмерном пространстве есть достоверное событие и, следовательно, его вероятность равна единице.
Волновая функция должна удовлетворять стандартным (естественным) условиям, находящимся в соответствии с ее вероятностной трактовкой:
1)быть конечной;
2)однозначной;
3)непрерывной;
4)гладкой, т.е. без изломов во всем пространстве, даже в тех точках (линиях, поверхностях), где потенциальная энергия терпит разрыв.
Дополнительно отметим, что частные производные волновой функции
∂Ψ |
∂Ψ |
∂Ψ |
∂x , |
∂y |
и ∂z могут терпеть разрыв только в тех точках пространства, |
где потенциальная функция, описывающая силовое поле, в котором движется частица, испытывает разрыв второго рода (случай задач с идеализированными силовыми полями).
Волновая функция полностью характеризует состояние микрообъекта (элементарной частицы, атома, молекулы). В квантовой механике можно вычислить средние значения физических величин, которые характеризуют данный микрообъект, находящийся в состоянии, описываемом волновой функцией Ψ. Например, средним значением расстояния r будет величина
+∞ |
|
r = ∫ r Ψ 2 dV . |
(26.9) |
−∞
Среднее значение квадрата расстояния  r2
r2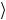 вычисляется аналогично:
вычисляется аналогично:
+∞ |
|
r2 = ∫ r2 Ψ 2 dV . |
(26.10) |
−∞
Сформулируем принцип суперпозиции квантовых состояний, которому должна удовлетворять волновая функция: если система может находиться
вразличных состояниях, описываемых волновыми функциями Ψ1, Ψ2, …,
Ψn, ..., то она также может находиться в состоянии, описываемом линей-
ной комбинацией этих функций:
82

Ψ = ∑CnΨn, |
(26.11) |
n |
|
|
|
где Cn |
(n =1, 2, 3, ...) – некоторые |
постоянные коэффициенты (в общем |
случае |
комплексные числа). Для |
нормированных волновых функций |
∑ Cn 2 =1.
n
Определив Ψ, можно далее найти и плотность вероятности ΨΨ* пребывания системы в этом состоянии. Подтверждением принципа суперпозиции (26.11) является согласие с опытом вытекающих из него следствий. Необходимо подчеркнуть, что принцип суперпозиции квантовых состояний лежит в основе физического содержания квантовой механики. С помощью этого принципа микроявления описываются без использования тех классических понятий, которые к ним неприменимы в квантовой области. При этом устраняется противоречие между корпускулярным и волновым описанием явлений.
26.7.Уравнения Шр¸дингера (временное и стационарное). Стационарные состояния. Квантование энергии
Основное динамическое уравнение нерелятивистской квантовой механики было предложено австрийским физиком Э. Шрёдингером в 1926 г. Как и уравнения движения Ньютона в классической механике, уравнение Шрёдингера постулируется. Следствия из уравнения Шрёдингера подтверждены экспериментально для атомных, молекулярных и ядерных явлений.
Уравнение Шрёдингера описывает изменение во времени состояния квантового объекта, характеризуемого волновой функцией. Если известна волновая функция Ψ в начальный момент времени, то, решая уравнение Шрёдингера, можно найти Ψ в любой последующий момент времени t.
Запишем уравнение Шрёдингера для частицы массой т, движущейся со скоростью, много меньшей скорости света в вакууме (v << c), под действием силы, порождаемой потенциаломU (x, y, z, t):
|
∂Ψ |
2 |
|
(26.12) |
|
|
|
||
i |
∂t = − |
|
ΔΨ +U Ψ, |
|
2m |
|
где i – мнимая единица (i2 = −1); = 2 = |
∂2 |
∂2 |
∂2 |
||||||
|
|
+ |
|
|
+ |
|
|
– оператор Ла- |
|
∂x |
2 |
∂y |
2 |
∂z |
2 |
||||
|
|
|
|
|
|
|
|||
пласа; Ψ(x,y,z,t) – временнаXя волновая функция частицы, которая зависит от координат и времени. Уравнение (26.12) содержит производную
83

от функции Ψ по времени и называется временным (нестационарным) уравнением Шрёдингера. В релятивистской области (v ~ c) уравнение Шрёдингера заменяется более сложным релятивистским уравнением Дирака.
Стационарными состояниями называют состояния, в которых все наблюдаемые физические величины не изменяются с течением времени. В частности, не изменяется со временем плотность вероятности Ψ(r,t) 2 . Стационарные решения уравнения Шрёдингера имеют смысл для тех задач, в которых силовое поле потенциально и, следовательно, потенциальная энергия U не зависит от времени: U =U (x, y,z) .
В стационарных состояниях состояние частицы в данный момент времени описывается периодической функцией времени Ψ с циклической частотой ω. При этом Ψ-функция определяется полной энергией частицы:
Ψ(r,t) = ψ(r )e−iωt , ω = |
E |
, |
(26.13) |
|
где функция ψ(r ) не зависит от времени, а выражение для частоты ω следует из соотношения, связывающего полную энергию Е частицы (в случае стационарного поля E = const) и частоту ω дебройлевской волны (26.1).
При таком виде Ψ-функции плотность вероятности Р остается постоянной:
P = ΨΨ* = ψ(r ) ψ*(r ). |
(26.14) |
Для нахождения невременноXй волновой функции ψ(r ) в стационарных состояниях подставим выражение (26.13) в уравнение Шрёдингера (26.12). Произведем дифференцирование выражения (26.13) по времени:
∂Ψ = ψ(r )(−iω)e−iωt .
∂t
Тогда из уравнения (26.12) с учетом выражения (26.13) имеем
|
iE |
|
2 |
|
|
|
i ψ − |
|
e−iEt |
= − |
|
e−iEt |
ψ +U ψe−iEt . |
|
|
|||||
|
|
|
|
2m |
|
|
Разделим правую и левую части уравнения на e−iEt и получим
и получим
|
2 |
|
-i2Eψ = − |
|
ψ +U ψ. |
|
||
|
2m |
|
Таким образом, выведено уравнение
2
Eψ = − 2m ψ +U ψ,
84
которое называют стационарным уравнением Шрёдингера и записывают в виде
Δψ + |
2m |
(E −U )ψ = 0. |
(26.15) |
2 |
|||
|
|
|
|
Это уравнение играет основную роль в атомной физике.
Отметим, что потенциальная энергия U (r ) здесь задается классически, т.е. как если бы никакими волновыми свойствами частица не обладала.
Квантование энергии. Учтем, что физический смысл имеют лишь такие решения уравнения (26.15), когда невременнаXя волновая функция ψ(r )
иее первые производные по координатам удовлетворяют стандартным условиям (см. подтему 26.4). Эти условия являются требованиями, накладываемыми на искомое решение дифференциального уравнения. Решения уравнения Шрёдингера (26.15), удовлетворяющие этим условиям,
оказываются возможными лишь при некоторых значениях энергии Е, называемых собственными значениями энергии. Функции ψ , являющиеся решениями уравнения (26.15) при этих значениях энергии, есть собственные функции, принадлежащие собственным значениям Е.
Собственные значения Е могут образовывать как непрерывный, так
идискретный ряд. В первом случае говорят о непрерывном (сплошном)
спектре энергии, во втором – о ее дискретном спектре.
Уравнение Шрёдингера является математическим выражением корпу- скулярно-волнового дуализма, согласно которому все существующие в природе частицы материи наделены также волновыми свойствами. Оно удовлетворяет принципу соответствия Бора (см. подтему 26.9) и в предельном случае, когда длина волны де Бройля значительно меньше размеров, характерных для рассматриваемого движения, позволяет описать движение
частиц по законам классической механики.
Релятивистское обобщение ψ-функции в квантовой механике было осуществлено П. Дираком для электрона в 1928 г. Основное уравнение релятивистской квантовой механики – уравнение Дирака – обобщает уравнение Шрёдингера и широко используется в квантовой электродинамике
итеории элементарных частиц.
26.8. Задачи на применение уравнения Шр¸дингера
При изложении основ квантовой механики рассматривают несколько типов задач, связанных с решением уравнения Шрёдингера. В задачах первого типа исследуется финитное (в ограниченной области пространства) движение микрообъекта, который находится в связанном состоянии. Например, движение электрона в заданном потенциальном поле
85

(в потенциальной «яме», см. рис. 26.5). Решая уравнение Шрёдингера (26.15), определяют спектр значений энергии микрообъекта и волновые функции стационарных микросостояний.
Взадачах второго типа рассматривается инфинитное (пространственно не ограниченное) движение микрообъекта во внешнем поле. Например, частица проходит сквозь потенциальный барьер (туннельный эффект, см. подтему 26.9) или рассеивается на некотором силовом центре. При таком движении энергетический спектр микрообъекта непрерывен. Решением уравнения Шрёдингера (26.15) рассчитывается вероятность рассеяния микрочастицы на заданный угол или вероятность ее прохождения сквозь барьер, а также отражения от него.
Взадачах третьего типа рассматривают изменение состояния микрообъекта во времени. Из уравнения Шрёдингера, зависящего от времени (26.13), находят вероятность того или иного квантового перехода, происходящего под влиянием заданного внешнего воздействия.
Движение свободной частицы. Решим стационарное уравнение Шрёдингера (26.15) для свободной частицы массой т, движущейся с импуль-
сом px в положительном направлении оси X (ось X направлена вдоль вектора v).
При свободном движении частицы ее полная энергия совпадает с кинетической, а скорость v = const. Поэтому потенциальную энергию частицы можно считать равной нулю: U (x) = 0. Тогда стационарное уравнение Шрёдингера (26.15) можно записать в виде дифференциального уравнения второго порядка:
d2ψ |
|
2m |
|
||
|
|
+ |
|
Eψ = 0. |
(26.16) |
dx |
2 |
2 |
|||
|
|
|
|
|
|
Прямой подстановкой можно убедиться в том, что частным решением уравнения является функция
ψ(x) = Aeikx, |
(26.16а) |
где А – некоторая постоянная; k – волновое число – может принимать любые положительные значения. Собственные значения энергии
2k2 |
|
E = 2m . |
(26.17) |
Функция ψ(x) = Aeikx – это координатная часть волновой функции Ψ(x,t) . Используем выражение (26.13), описывающее вид Ψ-функции в случае стационарных состояний. Получим, что решением временноXго уравнения Шрёдингера (26.12) будет волновая функция
86

Ψ(x,t) = Aexp(i k x − iωt) = Aexp(− |
i(Et − px x) |
). |
(26.18) |
|
Сравним решение (26.18) с уравнением плоской монохроматической волны (8.4), распространяющейся вдоль оси Х, записанным в экспоненциальной форме:
S = Aexp(−i(ωt − kx)).
Следовательно, свободно движущейся квантовой частице можно поставить в соответствие волну де Бройля. В частном случае движения вдоль оси Х она имеет вид плоской монохроматической волны (26.18). При этом вероятность местоположения свободной микрочастицы можно расписать как
dP dV = Ψ Ψ* = |
|
A |
|
2 = const, |
(26.18а) |
|
|
т.е. она не зависит от времени и одинакова во всех точках пространства (ось X). Определенная вероятность (26.18а) согласуется с соотношением
неопределенностей (26.2). Действительно, при выбранном |
px = 0 не- |
определенность координаты частицы x ~ (2 px ) → ∞, |
т.е. частица |
«размазана» равномерно по всему пространству. |
|
Из выражения (26.17) следует обычная для нерелятивистских частиц зависимость энергии от импульса:
p2 E = 2mx .
Таким образом, энергия свободной частицы может принимать любые значения от 0 до +∞, и ее энергетический спектр является непрерывным.
26.9. Частица в одномерной бесконечно глубокой потенциальной «яме»
Рассмотрим электрон, движущийся в потенциальном поле. Примером движения электрона в потенциальной «яме» является движение коллективизированных электронов внутри металла.
Потенциальная энергия электрона вне и внутри одномерной прямоугольной потенциальной «ямы» U (x) имеет следующие значения (рис. 26.5, а):
∞, x < 0; U (x) = 0, 0 ≤ x ≤ l;
∞, x > l,
87

а |
|
б |
|
в |
ψ |
|
г |
ψ (х) |
2 |
|
|
|
|
|
|
|
|||
U → ∞ U → ∞ n |
Е |
n |
n (х) |
Е |
n |
n |
Е |
||
|
|
3 |
E3 |
3 |
|
E3 |
3 |
|
E3 |
|
|
2 |
E2 |
2 |
|
E2 |
2 |
|
E2 |
0 |
l Х |
1 |
E1 |
1 |
|
E1 |
1 |
|
E1 |
0 |
l Х |
0 |
|
l Х |
0 |
|
l Х |
||
Рис. 26.5. Случай одномерного движения микрочастицы в бесконечно глубокой потенциальной «яме»:
а – бесконечно глубокая потенциальная «яма»; б – энергетический спектр Еп микрочастицы; в, г –
соответственно собственные функции ψп и плотность вероятности ψn 2 обнаружения микрочастицы в «яме»
где l – ширина «ямы»; стенки «ямы» бесконечно высокие, энергия отсчитывается от ее дна. Используем уравнение Шрёдингера для стационарных состояний (26.15). Для одномерного случая в пределах «ямы», где U = 0, это уравнение упрощается:
d2ψ |
|
2m |
|
d2ψ |
+ k2ψ = 0, |
|
|||
|
|
+ |
|
Eψ = 0 |
|
|
|
(26.19) |
|
dx |
2 |
2 |
dx |
2 |
|||||
|
|
|
|
|
|
|
|
||
где k2 = 2mE 2 .
2 .
Общее решение уравнения (26.19) ψ(x) = asin(kx +α)+bcos(kx +α) для
рассматриваемого случая (рис. 26.5) принимает вид |
|
ψ(x) = asin(kx + α), |
(26.20) |
где а и α – произвольные постоянные.
Функция ψ(x) должна удовлетворять стандартным условиям. Видно, что ψ(x) в виде (26.20) однозначна и конечна. Она должна быть еще и непрерывной. За пределы «ямы» частица не проникает из-за бесконечно высоких стенок, поэтому волновая функция вне «ямы» равна нулю. Следовательно, на границах «ямы» непрерывная волновая функция также должна обращаться в нуль:
ψ(0) = ψ(l) = 0.
Из граничного условия ψ(0) = asinα = 0 получаем, что
α = ±πm′,
где m′ = 0,1, 2, 3, ... . При m′ = 0, а также при четных значениях m′ имеем ψ(x) = asin kx. При нечетных значениях m′ получаем ψ(x) = −asin kx.
88

Поскольку физический смысл имеет квадрат модуля волновой функции ψ(x) 2 , который от выбора значения m′, т.е. от знака ψ(x), не зависит, то без потери общности можно считать, что α = 0.
Из граничного условия ψ(l) = asin kl = 0 следует, что при a ≠ 0
kl = ±πn, |
(26.20а) |
где n =1, 2, 3, ... (п = 0 отпадает, так как при этом ψ = 0 – частицы в «яме» нет). Число k принимает лишь определенные дискретные значения, удовлетворяющие условию (26.20а). Отсюда
k = |
πn |
(26.21) |
|
l |
|
и можно заключить, что поскольку по определению k = 2π λ , где λ – дли-
|
2π |
= |
πn |
|
l = |
λ |
на волны де Бройля для электрона в «яме», то |
|
|
2 n. |
|||
λ |
l |
Таким образом, на ширине потенциальной «ямы» должно укладываться целое число полуволн де Бройля. Используем теперь выражение (26.19) и получим уравнение для собственных значений энергии En:
|
2π2 |
|
|
||
En = |
|
|
n2 |
, n =1, 2, 3, ... . |
(26.22) |
2ml |
2 |
||||
|
|
|
|
|
|
Отрицательные значения п приводят лишь к изменению знака псифункции и не дают новых состояний. При этом минимальное значение энергии частицы в «яме» не равно нулю:
2π2 Emin = 2ml2 .
Следовательно, энергия частицы в бесконечно глубокой потенциальной «яме» принимает лишь определенные дискретные значения, т.е. квантуется, ее спектр – дискретный (рис. 26.5, б), в то время как классическая механика на энергию частицы в этом случае таких ограничений не накладывает.
Другие значения Е энергии электрона, кроме En , невозможны: вероятность обнаружить внутри «ямы» электрон с энергией, отличной от En , равна нулю, так как при E ≠ En решение уравнения (26.19) только нулевое.
Квантованные значения энергии Еп называются уровнями энергии, а число п, определяющее энергетические уровни частицы, называется квантовым числом. Расстояние между соседними уровнями энергии (26.22)
|
|
|
2π2 |
|
||
En |
= En+1 − En |
= |
|
|
(2n +1). |
(26.22а) |
|
2 |
|||||
|
|
2ml |
|
|
|
|
89

Отношение En к En зависит от квантового числа следующим образом:
En |
= |
2n +1 |
(26.22б) |
|
|
|
. |
||
En |
n2 |
|||
В 1923 г. Н. Бор сформулировал принцип соответствия: при больших квантовых числах выводы и результаты квантовой механики должны соответствовать классическим результатам.
Собственные волновые функции согласно (26.20) можно записать как
|
|
|
πn |
≤ x ≤ l; |
ψn |
asin |
x, 0 |
||
(x) = |
|
l |
|
|
|
|
x |
< 0, x > l. |
|
|
0, |
|||
l
Учтем условие нормировки (26.8), согласно которому ∫ ψ(x) 2 dx =1,
и тогда |
|
|
|
|
|
|
0 |
|
l |
πn |
|
a2 |
l |
2πn |
|
a2 |
|
∫a2 sin2 |
l |
x dx = |
|
∫(1− cos |
l |
x)dx = |
|
l =1. |
2 |
2 |
|||||||
0 |
|
|
|
0 |
|
|
|
|
Следовательно, a = 2 l . Таким образом, нормированные собственные функции в данном случае имеют вид (рис. 26.5, в)
l . Таким образом, нормированные собственные функции в данном случае имеют вид (рис. 26.5, в)
|
|
2 |
|
πn |
|
|
|
|
|
|
|
x, 0 ≤ x ≤ l, n =1, 2, 3, ... |
|
Ψn |
(x) = |
l sin |
l |
(26.23) |
||
|
|
x < 0, |
x > l. |
|
||
|
0, |
|
||||
Также на рис. 26.5, г изображена плотность вероятности Р обнаружения частицы на разных расстояниях от стенок «ямы», определяемая выражением
P = ψn(x) 2 = ψn(x) ψ*n(x).
Из этих графиков видно, что в низшем энергетическом состоянии (n =1) с наибольшей вероятностью частицу можно обнаружить в середине «ямы», а вероятность нахождения ее вблизи краев «ямы» весьма мала. В состоянии с n = 2 частица не может быть обнаружена в середине «ямы» и с одинаковой вероятностью бывает как в левой, так и в правой половине «ямы». Такое поведение частицы резко отличается от поведения классической частицы. Если классическая частица в подобной «яме» движется с постоянной скоростью, то вероятность ее обнаружения во всех точках будет одинакова.
90
